Конфигурация — различия между версиями
м |
|||
| Строка 1: | Строка 1: | ||
| + | <wikitex> | ||
{{В разработке}} | {{В разработке}} | ||
__TOC__ | __TOC__ | ||
== Общие определения(R^d) == | == Общие определения(R^d) == | ||
| − | + | ||
{{Определение | {{Определение | ||
|id=hyperplane | |id=hyperplane | ||
| Строка 33: | Строка 34: | ||
}} | }} | ||
| − | == | + | == Плоскость(R^2) == |
| + | |||
| + | На $\mathbb{R}^2$ можно ввести обобщение — вместо линий(гиперплоскости в $\mathbb{R}^2$) можно брать монотонные по x(то есть каждая параллельная оси y линия пересекает её не более, чем в 1 точке) Жордановы дуги, причём такие что максимально количество взаимопересечений каждой пары дуг такого множества — заранее зафиксированная константа. Засчёт этого ограничения отсеиваются такие пары дуг как, например, $y = \sin(x)$ и $y = \cos(x)$. А вот пару дуг $y = \cos(x)$ и $y = x^2$ можно взять. | ||
| + | |||
| + | Также ячейками размерности 0 считаются точки, ограничивающие эти дуги. | ||
| − | + | Но для упрощения реализаций алгоритмов мы всё же ограничимся использованием прямых, лучей и отрезков. | |
=== Примеры === | === Примеры === | ||
| − | + | Возьмём $\mathcal{H} = \{AB, CD, EF, a\}$. | |
{|align="left" | {|align="left" | ||
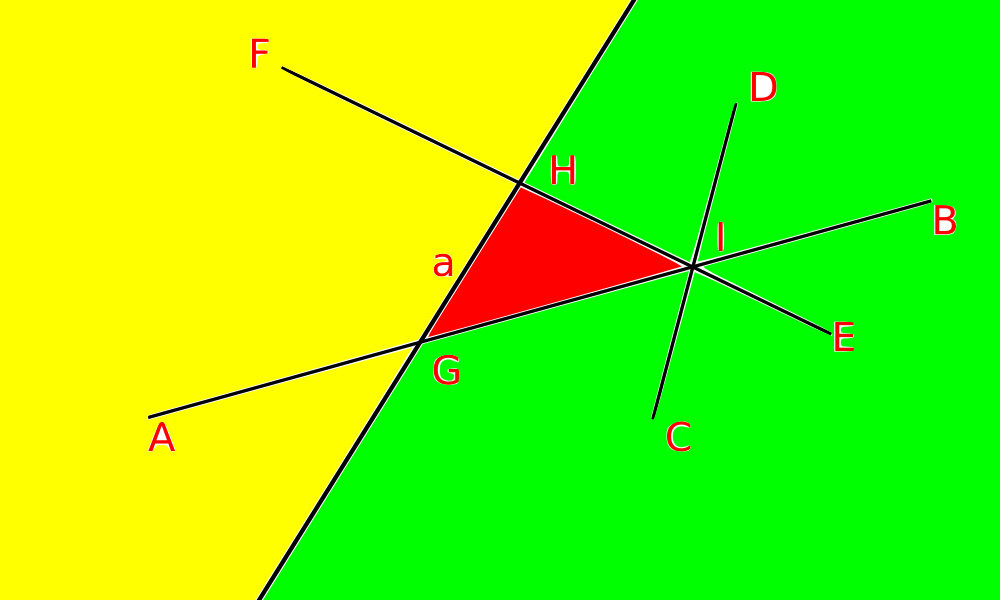
| [[Файл:cell2.png | 320x200 px | frame | Цветами выделены ячейки размерности 2. Жёлтая и зелёная ячейки не ограничены, синяя - ограничена.]] | | [[Файл:cell2.png | 320x200 px | frame | Цветами выделены ячейки размерности 2. Жёлтая и зелёная ячейки не ограничены, синяя - ограничена.]] | ||
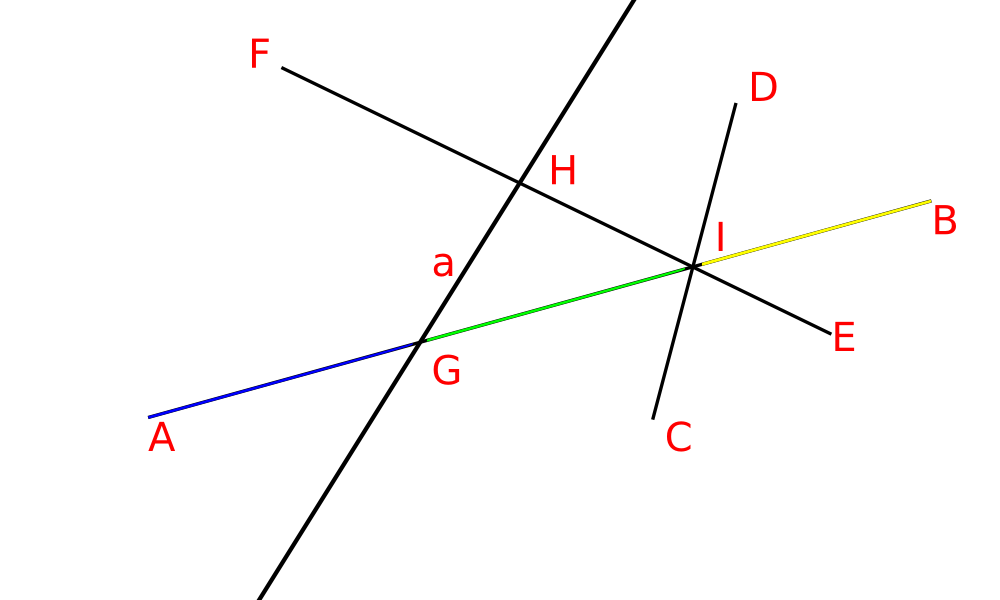
| [[Файл:cell1.png | 320x200 px | frame | Взяв множество S с единственным отрезком AB, получим три ячейки размерности 1. Взяв за множество S поочерёдно CD, EF и a, получим остальные ячейки размерности 1.]] | | [[Файл:cell1.png | 320x200 px | frame | Взяв множество S с единственным отрезком AB, получим три ячейки размерности 1. Взяв за множество S поочерёдно CD, EF и a, получим остальные ячейки размерности 1.]] | ||
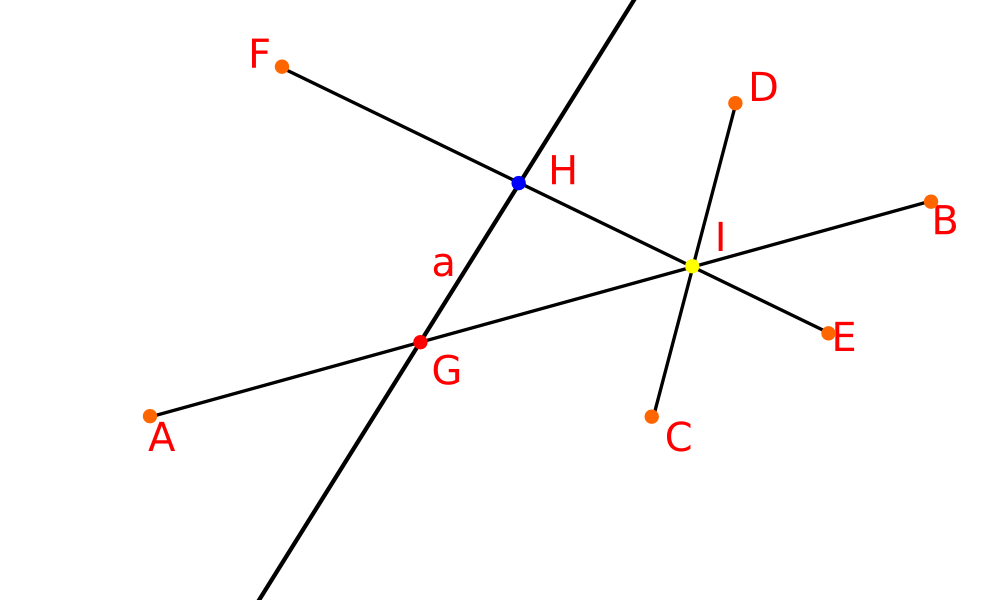
| − | | [[Файл:cell0.png | 320x200 px | frame | Взяв поочерёдно за множество S множества {a, EF}, {a, AB}, {AB, CD, EF}, получим ячейки G, H и I размерности 0. Как было замечено, точки A, B, C, D, E, F также ячейки размерности 0 как органичивающие отрезки.]] | + | | [[Файл:cell0.png | 320x200 px | frame | Взяв поочерёдно за множество S множества {a, EF}, {a, AB}, {AB, CD, EF}, получим ячейки G, H и I размерности 0. Как было замечено, точки A, B, C, D, E, F — также ячейки размерности 0 как органичивающие отрезки.]] |
|} | |} | ||
Версия 04:33, 2 ноября 2011
<wikitex>
Общие определения(R^d)
| Определение: |
| Гиперплоскостью(англ. hyperplane) в $\mathbb{R}^d$ называется его подпространство размерности $\mathbb{R}^{d - 1}$. |
| Определение: |
| Конфигурацией(англ. arrangement) $\mathcal{A}(\mathcal{H})$ называется разбиение $\mathbb{R}^d$ в связные открытые(топологически) ячейки размерностей $0, 1 \dots d $ множеством $\mathcal{H}$ гиперплоскостей в $ \mathbb{R}^d$. |
| Определение: |
| Ячейкой(англ. cell) размерности $d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в $R^d$, не пересекаемая ни одной гиперплоскостью в $\mathcal{H}$. Ячейкой размерности $k$, где $0 \le k < d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в пересечении гиперплоскостей подмножества $\mathcal{S} \in \mathcal{H}$, которая не пересекается ни одной гиперплоскостью из множества $\mathcal{H} \setminus \mathcal{S}$. //БИДА, сложно обобщить на ограниченные гиперплоскости. |
| Определение: |
| Вершина(англ. vertex) — ячейка размерности 0. Ребро(англ. edge) — ячейка размерности 1. |
Плоскость(R^2)
На $\mathbb{R}^2$ можно ввести обобщение — вместо линий(гиперплоскости в $\mathbb{R}^2$) можно брать монотонные по x(то есть каждая параллельная оси y линия пересекает её не более, чем в 1 точке) Жордановы дуги, причём такие что максимально количество взаимопересечений каждой пары дуг такого множества — заранее зафиксированная константа. Засчёт этого ограничения отсеиваются такие пары дуг как, например, $y = \sin(x)$ и $y = \cos(x)$. А вот пару дуг $y = \cos(x)$ и $y = x^2$ можно взять.
Также ячейками размерности 0 считаются точки, ограничивающие эти дуги.
Но для упрощения реализаций алгоритмов мы всё же ограничимся использованием прямых, лучей и отрезков.
Примеры
Возьмём $\mathcal{H} = \{AB, CD, EF, a\}$.
Источники
- Goodman J.E., O'Rourke J. Handbook of discrete and computational geometry. p. 537, 2004, 2nd edition.
</wikitex>