Недетерминированные конечные автоматы — различия между версиями
(fix) |
м (fixes) |
||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Недетерминированный конечный автомат''' (НКА) {{---}} | + | '''Недетерминированный конечный автомат''' (НКА) {{---}} пятерка <tex>\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to 2^Q \rangle</tex>, где <tex>\Sigma</tex> {{---}} алфавит, <tex>Q</tex> {{---}} множество состояний автомата, <tex>s</tex> {{---}} начальное состояние автомата, <tex>T</tex> {{---}} множество допускающих состояний автомата, <tex>\delta</tex> {{---}} функция переходов. |
| − | Таким образом единственное отличие НКА от ДКА {{---}} | + | Таким образом единственное отличие НКА от ДКА {{---}} существование нескольких переходов по одному символу из одного состояния. |
}} | }} | ||
| Строка 8: | Строка 8: | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | '''Мгновенная кофигурация''' {{---}} | + | '''Мгновенная кофигурация''' {{---}} пара <tex> \langle p, q \rangle </tex>, <tex> p \in Q </tex>, <tex> q \in \Sigma^*</tex>}} |
Определим некоторые операции для мгновенных конфигураций. | Определим некоторые операции для мгновенных конфигураций. | ||
| Строка 50: | Строка 50: | ||
[[Файл:NKA_1.jpg]] | [[Файл:NKA_1.jpg]] | ||
| − | == Алгоритм определяющий допустимость автоматом слова == | + | == Алгоритм, определяющий допустимость автоматом слова == |
| − | + | Этот алгоритм решает такую задачу: заданы НКА и слово, нужно определить допускает ли НКА данное слово. По сравнению с ДКА, определять допускает ли НКА слово сложнее, так как из состояния теперь есть несколько переходов по букве и выбрать случайный переход нельзя. | |
| − | По сравнению с ДКА, определять допускает ли НКА слово сложнее, так как из состояния теперь есть несколько переходов по букве и выбрать случайный переход нельзя. | ||
Поступим по-другому, определим множество всех достижимых состояний из стартового по слову <tex> \alpha </tex>. | Поступим по-другому, определим множество всех достижимых состояний из стартового по слову <tex> \alpha </tex>. | ||
* <tex> R(\alpha) = \lbrace p | \langle s, \alpha \rangle \vdash^* \langle p, \varepsilon \rangle \rbrace </tex> | * <tex> R(\alpha) = \lbrace p | \langle s, \alpha \rangle \vdash^* \langle p, \varepsilon \rangle \rbrace </tex> | ||
| Строка 76: | Строка 75: | ||
accepts = False | accepts = False | ||
for <tex> t \in T </tex> do | for <tex> t \in T </tex> do | ||
| − | if | + | if <tex> t \in R_{|w|} </tex> then |
accepts = True | accepts = True | ||
</font> | </font> | ||
| + | |||
| + | Время работы этого алгоритма будет <tex> \mathop O(|w|\sum\limits_{t \in Q} \sum\limits_{c \in \Sigma} |\delta(t, c)|) </tex> | ||
== См. также == | == См. также == | ||
* [[Детерминированные конечные автоматы]] | * [[Детерминированные конечные автоматы]] | ||
| + | * [[Построение по НКА эквивалентного ДКА, алгоритм Томпсона]] | ||
| + | |||
| + | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Автоматы и регулярные языки]] | ||
Версия 02:16, 14 ноября 2011
| Определение: |
| Недетерминированный конечный автомат (НКА) — пятерка , где — алфавит, — множество состояний автомата, — начальное состояние автомата, — множество допускающих состояний автомата, — функция переходов. Таким образом единственное отличие НКА от ДКА — существование нескольких переходов по одному символу из одного состояния. |
Содержание
Процесс допуска
| Определение: |
| Мгновенная кофигурация — пара , , |
Определим некоторые операции для мгновенных конфигураций.
| Определение: |
Говорят, что выводится за один шаг из , если:
|
| Определение: |
| Говорят, что выводится за ноль и более шагов из , если :
|
| Определение: |
| НКА допускает слово , если . |
Менее формально это можно описать так: НКА допускает слово , если существует путь из начального состояния в какое-то терминальное, такое что буквы, выписанные с переходов на этом пути по порядку, образуют слово .
Язык автомата
| Определение: |
| Множество слов, допускаемых автоматом , называется языком НКА .
|
Язык НКА тоже является автоматным языком, так как можно построить из НКА эквивалентный ДКА, поэтому вычислительная мощность этих двух автоматов совпадает.
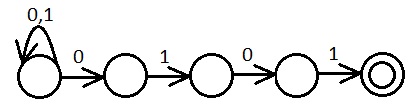
Пример
Автомат, допускающий слова над алфавитом из символов 0 и 1, допускающий слова оканчивающиеся на 0101.
(0|1)*0101
Алгоритм, определяющий допустимость автоматом слова
Этот алгоритм решает такую задачу: заданы НКА и слово, нужно определить допускает ли НКА данное слово. По сравнению с ДКА, определять допускает ли НКА слово сложнее, так как из состояния теперь есть несколько переходов по букве и выбрать случайный переход нельзя. Поступим по-другому, определим множество всех достижимых состояний из стартового по слову .
Пусть нам нужно определить допускает ли НКА слово . Заметим, что если , то слово допускается, так как по определению . Алгоритм состоит в том, чтобы построить .
Очевидно, что . Пусть мы построили , как же получить , где . Заметим, что
- ,
так как
- ,
Теперь, когда мы научились добавлять символ к строке, возьмем , будем добавлять и находить для каждого .
Когда мы получим , проверим что в нем есть терминальное состояние.
Псевдокод:
for i = 1 to length(w) do for do accepts = False for do if then accepts = True
Время работы этого алгоритма будет