Коды Грея — различия между версиями
Gromak (обсуждение | вклад) м |
Gromak (обсуждение | вклад) |
||
| Строка 10: | Строка 10: | ||
== Алгоритм построения == | == Алгоритм построения == | ||
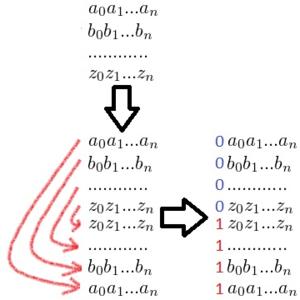
| − | [[Файл:Gray_Code. | + | [[Файл:Gray_Code.png|thumb|right|Иллюстрация получения зеркального двоичного кода Грея.]] |
Существует несколько видов Кода Грея, самый простой из них {{---}} так называемый зеркальный двоичный Код Грея. Строится он так: | Существует несколько видов Кода Грея, самый простой из них {{---}} так называемый зеркальный двоичный Код Грея. Строится он так: | ||
Версия 05:26, 16 декабря 2011
Содержание
Определение
| Определение: |
| Код Грея (Gray code) — такое упорядочение -ичных (обычно двоичных) векторов, что соседние вектора отличаются только в одном разряде. |
Код назван в честь Фрэнка Грея, который в 1947-ом году получил патент на "отражённый двоичный код". Изначально он предназначался для избавления от паразитных состояний в электромеханических переключателях, однако сейчас область его применения гораздо шире.
Алгоритм построения
Существует несколько видов Кода Грея, самый простой из них — так называемый зеркальный двоичный Код Грея. Строится он так:
Для получения кода длины производится шагов. На первом шаге код имеет длину 1 и состоит из двух векторов (0) и (1). На каждом следующем шаге в конец списка заносятся все уже имеющиеся вектора в обратном порядке, и затем к первой половине получившихся векторов дописывается "0", а ко второй "1". С каждым шагом длина векторов увеличивается на 1, а их количество — вдвое. Таким образом, количество векторов длины равно
Псевдокод
|
GrayCode — двумерный массив, в котором GrayCode[a, b] — -ый бит в -ом коде Грея. buildCode(n):
GrayCode[1, n] = 0
GrayCode[2, n] = 1 {построение кода длины 1}
p = 2 {p — количество уже имеющихся кодов}
for (i = 2, i <= n, i++):
p = p * 2
for (k = i + 1, k <= 2 * i, k++):
GrayCode[k] = GrayCode[p + 1 - k] {отражение имеющихся кодов}
GrayCode[k - i, n + 1 - i] = 0
GrayCode[k, n + 1 - i] = 1 {добавление 0 и 1 в начало}
|
Доказательство правильности работы алгоритма
По индукции:
- на первом шаге код отвечает условиям
- предположим, что код, получившийся на -ом шаге, является Кодом Грея
- тогда на шаге : первая половина кода будет корректна, так как она совпадает с кодом с шага за исключением добавленного последнего бита 0. Вторая половина тоже соответствует условиям, так как она является зеркальным отражением первой половины, только добавлен везде бит 1. На стыке: первые бит совпадают в силу зеркальности, последние различны по построению.
Таким образом, этот код — Код Грея. Индукционное предположение доказано, алгоритм работает верно.
Этот алгоритм можно обобщить и для -ичных векторов. Также известен алгоритм преобразования двоичного кода в Код Грея.
Существует ещё несколько видов Кода Грея — сбалансированный Код Грея, код Беккета-Грея, одноколейный Код Грея.
Явная формула для получения зеркального двоичного кода Грея
| Теорема: |
В двоичном зеркальном коде Грея -ый код может быть получен по формуле при нумерации кодов с нуля. |
| Доказательство: |
|
Для кода длиной 1 бит утверждение проверяется непосредственно. Пусть существует зеркальный двоичный код Грея длины , для которого выполнено, что для любого Обозначим за код длины , полученный из описанным выше алгоритмом. Тогда: Для любого Для любого , где , то есть
Таким образом, шаг индукции доказан, следовательно, теорема верна. |
Применение
Код Грея применяется в:
- датчиках-энкодерах (устройства, преобразующие угол поворота вала в электрический сигнал)
- как способ решения задачи о Ханойских башнях (дано три стержня, на первом из них нанизано 8 колец разного размера в виде пирамиды; цель — перенести пирамиду на другой стержень, сохранив упорядоченность);
- в генетических алгоритмах
- в Картах Карно (при передаче в карту переменные сортируются в Код Грея)
- в кодах, исправляющих ошибки
- для связи систем с различной частотой работы.