Формула Эйлера — различия между версиями
VVolochay (обсуждение | вклад) |
VVolochay (обсуждение | вклад) |
||
| Строка 6: | Строка 6: | ||
<br/><tex>V - E + F = 2</tex> | <br/><tex>V - E + F = 2</tex> | ||
|proof= | |proof= | ||
| − | + | ||
| − | + | ||
Воспользуемся методом математической индукции по количеству граней графа. | Воспользуемся методом математической индукции по количеству граней графа. | ||
<br /> | <br /> | ||
| Строка 17: | Строка 17: | ||
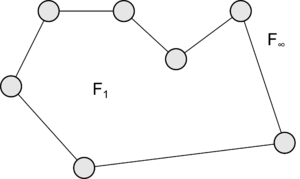
Покажем, что если теорема верна для графов с <tex>F</tex> гранями, то она будет верна и для графов с <tex>F + 1</tex> гранями. Пусть <tex>G</tex> - плоский граф, имеющий <tex>V</tex> вершин, <tex>E</tex> ребер и <tex>F</tex> граней, и для него справедлива формула Эйлера. Добавим новую грань (пунктирная линия на рис.2), проводя по внешней грани <tex>F_{\infty}</tex> некоторую элементарную цепь, соединяющую две вершины максимального цикла графа <tex>G</tex>. Если эта цепь имеет <tex>r</tex> ребер, то необходимо добавить <tex>r - 1</tex> новых вершин и одну новую грань. Ясно, что формула Эйлера останется справедливой и для нового графа, так как <tex>V' - E' + F' = (V + r - 1) - (E + r) + (F + 1) = V - E + F</tex> | Покажем, что если теорема верна для графов с <tex>F</tex> гранями, то она будет верна и для графов с <tex>F + 1</tex> гранями. Пусть <tex>G</tex> - плоский граф, имеющий <tex>V</tex> вершин, <tex>E</tex> ребер и <tex>F</tex> граней, и для него справедлива формула Эйлера. Добавим новую грань (пунктирная линия на рис.2), проводя по внешней грани <tex>F_{\infty}</tex> некоторую элементарную цепь, соединяющую две вершины максимального цикла графа <tex>G</tex>. Если эта цепь имеет <tex>r</tex> ребер, то необходимо добавить <tex>r - 1</tex> новых вершин и одну новую грань. Ясно, что формула Эйлера останется справедливой и для нового графа, так как <tex>V' - E' + F' = (V + r - 1) - (E + r) + (F + 1) = V - E + F</tex> | ||
}} | }} | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:Eulerformul1.png|300px|thumb|рис. 1]] | ||
| + | |[[Файл:Eulerformul2.png|300px|thumb|рис. 2]] | ||
| + | |} | ||
| + | |||
{{Теорема | {{Теорема | ||
|id=EulerFormulaCons | |id=EulerFormulaCons | ||
Версия 00:32, 15 марта 2012
| Теорема (Формула Эйлера): |
| Доказательство: |
|
Воспользуемся методом математической индукции по количеству граней графа.
|
| Теорема (Следствие из формулы Эйлера): |
Пусть связный планарный обыкновенный граф с вершинами (), ребрами и гранями. Тогда |
| Доказательство: |
| Поскольку не содержит петель и кратных ребер, то каждая грань граничит хотя бы с тремя ребрами. Пусть, двигаясь вдоль -й грани мы пройдем ребер. Очевидно, что . Поскольку , получаем . Из формулы Эйлера , то есть . |
Литература
- Асанов М,, Баранский В., Расин В. - Дискретная математика - Графы, матроиды, алгоритмы
- О.Оре - Графы и их применение