Теорема Понтрягина-Куратовского — различия между версиями
| Строка 8: | Строка 8: | ||
Граф [[Укладка_графа_на_плоскости| планарен]] тогда и только тогда, когда он не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex> . | Граф [[Укладка_графа_на_плоскости| планарен]] тогда и только тогда, когда он не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex> . | ||
|proof = | |proof = | ||
| − | Возьмем укладку графа <tex> G_1 </tex>. Добавив на нужных ребрах вершины степени <tex> 2 </tex> и удалив некотрые вершины степени <tex> 2 </tex> в старом графе получим укладку гомеоморфного графа <tex> G_2 </tex> | + | Возьмем укладку графа <tex> G_1 </tex>. Добавив на нужных ребрах вершины степени <tex> 2 </tex> и удалив некотрые вершины степени <tex> 2 </tex> в старом графе, получим укладку гомеоморфного графа <tex> G_2 </tex>. Следовательно из планарности графа следует планарность гомеморфного графа и наоборот. |
| − | + | Поэтому доказательство необходимости можно посмотреть [[Непланарность_K5_и_K3,3| здесь]], докажем достаточность. | |
От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex>. | От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex>. | ||
| Строка 18: | Строка 18: | ||
Если <tex> G </tex> не [[Отношение_связности,_компоненты_связности|связен]], то в силу минимальности <tex> G </tex> его компоненты связности планарны и, следовательно, сам граф <tex> G </tex> планарен. | Если <tex> G </tex> не [[Отношение_связности,_компоненты_связности|связен]], то в силу минимальности <tex> G </tex> его компоненты связности планарны и, следовательно, сам граф <tex> G </tex> планарен. | ||
=== G — обыкновенный граф === | === G — обыкновенный граф === | ||
| − | В самом деле, пусть в графе <tex> G </tex> есть петля или кратное ребро <tex> e </tex>. | + | В самом деле, пусть в графе <tex> G </tex> есть петля или кратное ребро <tex> e </tex>. Тогда в силу минимальности <tex> G </tex> граф <tex> G - e </tex> планарен. Добавляя ребро <tex> e </tex> к графу <tex> G - e </tex> получим, что граф <tex> G </tex> планарен. |
=== G — [[Отношение_вершинной_двусвязности|блок]] === | === G — [[Отношение_вершинной_двусвязности|блок]] === | ||
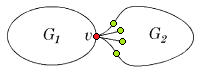
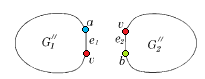
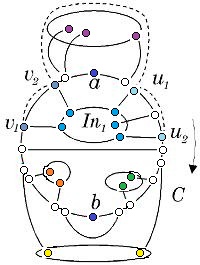
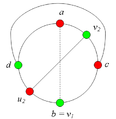
Пусть, от противного, в графе есть [[Точка_сочленения,_эквивалентные_определения|точка сочленения]] <tex> v </tex>. Через <tex> G_1 </tex> обозначим подграф графа <tex> G </tex>, порождённый вершинами одной из компонент связности графа <tex> G - v</tex> и вершинной <tex> v </tex>, а через | Пусть, от противного, в графе есть [[Точка_сочленения,_эквивалентные_определения|точка сочленения]] <tex> v </tex>. Через <tex> G_1 </tex> обозначим подграф графа <tex> G </tex>, порождённый вершинами одной из компонент связности графа <tex> G - v</tex> и вершинной <tex> v </tex>, а через | ||
<tex> G_2 </tex> подграф графа <tex> G </tex>, порождённый вершинами остальных компонент связности графа <tex> G - v </tex> и вершиной <tex> v </tex>. (рис. 1) | <tex> G_2 </tex> подграф графа <tex> G </tex>, порождённый вершинами остальных компонент связности графа <tex> G - v </tex> и вершиной <tex> v </tex>. (рис. 1) | ||
| − | В силу минимальности <tex> G </tex>,<tex> G_1 </tex> и <tex> G_2 </tex> - планарны. | + | В силу минимальности <tex> G </tex>, <tex> G_1 </tex> и <tex> G_2 </tex> - планарны. |
[[Файл:New.p-k.1.png|thumb|right|рис. 1]] | [[Файл:New.p-k.1.png|thumb|right|рис. 1]] | ||
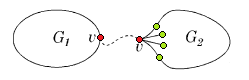
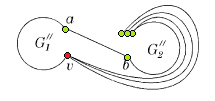
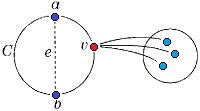
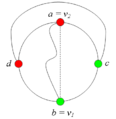
Возьмём укладку графа <tex> G_1 </tex> на плоскости такую, что вершина <tex> v </tex> лежит на границе внешней грани. Ее можно получить, взяв любую укладку <tex> G_1 </tex> на плоскости, по ней построив укладку на шаре, используя обратную [http://en.wikipedia.org/wiki/Stereographic_projection стереографическую проекцию], потом повернуть сферу так, чтоб <tex> v </tex> оказалась на внешней грани стереографической проекции повернутого шара. | Возьмём укладку графа <tex> G_1 </tex> на плоскости такую, что вершина <tex> v </tex> лежит на границе внешней грани. Ее можно получить, взяв любую укладку <tex> G_1 </tex> на плоскости, по ней построив укладку на шаре, используя обратную [http://en.wikipedia.org/wiki/Stereographic_projection стереографическую проекцию], потом повернуть сферу так, чтоб <tex> v </tex> оказалась на внешней грани стереографической проекции повернутого шара. | ||
Версия 22:35, 19 марта 2012
Содержание
| Определение: |
| Граф гомеоморфен , если можно получить из с помощью конечного числа применений процедур включения и исключения вершин степени 2. |
| Теорема: | ||||||||||||||||||||||||||||||||
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных или . | ||||||||||||||||||||||||||||||||
| Доказательство: | ||||||||||||||||||||||||||||||||
|
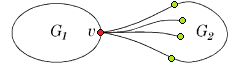
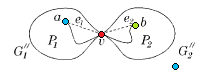
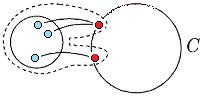
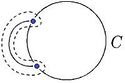
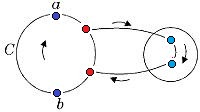
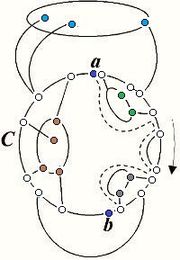
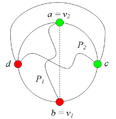
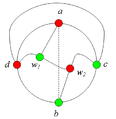
Возьмем укладку графа . Добавив на нужных ребрах вершины степени и удалив некотрые вершины степени в старом графе, получим укладку гомеоморфного графа . Следовательно из планарности графа следует планарность гомеморфного графа и наоборот. Поэтому доказательство необходимости можно посмотреть здесь, докажем достаточность. От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных или . Пусть — такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. G связенЕсли не связен, то в силу минимальности его компоненты связности планарны и, следовательно, сам граф планарен. G — обыкновенный графВ самом деле, пусть в графе есть петля или кратное ребро . Тогда в силу минимальности граф планарен. Добавляя ребро к графу получим, что граф планарен. G — блокПусть, от противного, в графе есть точка сочленения . Через обозначим подграф графа , порождённый вершинами одной из компонент связности графа и вершинной , а через подграф графа , порождённый вершинами остальных компонент связности графа и вершиной . (рис. 1) В силу минимальности , и - планарны. Возьмём укладку графа на плоскости такую, что вершина лежит на границе внешней грани. Ее можно получить, взяв любую укладку на плоскости, по ней построив укладку на шаре, используя обратную стереографическую проекцию, потом повернуть сферу так, чтоб оказалась на внешней грани стереографической проекции повернутого шара. Затем во внешней грани графа возьмём укладку графа такую, что вершина будет представлена на плоскости в двух экземплярах. (рис. 2) Соединим два экземпляра вершины пучком жордановых линий, не допуская лишних пересечений с укладками графов и , состоящим из такого количества линий, какова степень вершины в графе . Далее отбросим вхождение вершины в граф , заменяя инцидентные ей рёбра на жордановы линии, полученные из линий указанного пучка и рёбер (рис. 3) Таким образом мы получили укладку графа на плоскости, что невозможно. В G нет мостовГраф не равен и в нем нет точек сочленения, следовательно в нет мостов. В G' существует цикл, содержащий вершины a и bПусть — произвольное ребро графа , .
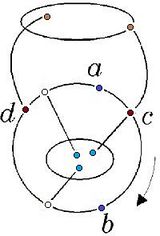
Пусть и лежат в одном блоке графа .
Заметим, что в графе рёбер меньше, чем в графе . Действительно, вместо ребра в есть ребро и часть рёбер из графа осталась в графе . Аналогично, в графе рёбер меньше, чем в графе . Отметим, что опять вершина представлена на плоскости в двух экземплярах. Очевидно, добавление ребра не меняет планарности графа . Склеим оба вхождения вершины точно так же, как это мы сделали в предыдущем пункте доказательства (рис. 6). Сотрем затем ранее добавленные ребра и . В результате мы получим укладку графа на плоскости, что невозможно. Утверждение доказано. Вспомогательные определения и утверждение об одновременно разделяющейся внутренней частиСреди всех укладок графа на плоскости и среди всех циклов , содержащих и , зафиксируем такую укладку и такой цикл, что внутри области, ограниченной циклом , лежит максимальное возможное число граней графа . Зафиксируем один из обходов по циклу (на рисунках будем рассматривать обход по часовой стрелке по циклу ). Для вершин и цикла через будем обозначать простую -цепь, идущую по циклу от до в направлении обхода цикла. Конечно, . Положим {}, т.е. получено из отбрасыванием вершин и .
В силу связности графа для любой внешней компоненты должны существовать рёбра в , соединяющие её с вершинами цикла .
В силу связности графа для любой внутренней компоненты должны существовать рёбра в , соединяющие её с вершинами цикла .
Будем говорить, что внешняя (внутренняя) часть встречает цикл в своих точках прикрепления к циклу .
Аналогично можно ввести понятие -разделяющей внутренней части. Заметим, что внутрення часть может встречать цикл , вообще говоря, более чем в двух точках, но не менее чем в двух точках.
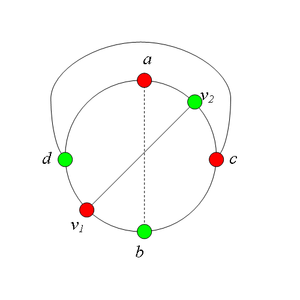
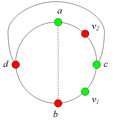
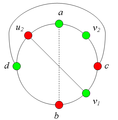
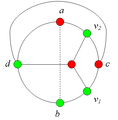
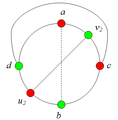
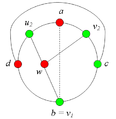
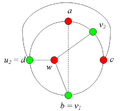
Разбор случаев взаимного положения a, b, c, d, u1, u2, v1, v2Рассмотрим 2 случая. 1. Пусть пара вершин и является -разделяющей. 2. Пусть пара вершин и не является -разделяющей. 2.1. Пусть и лежат на , т.е. и (рис. 7.2). 2.1.1 Пусть лежит на . 2.1.2. Пусть . 2.1.3. Пусть лежит на . Теперь рассмотрим случаи, когда хотя бы одна из вершин и не лежит на . Без ограничения общности будем считать, что это вершина , т.е (поскольку лежит на ). 2.2. Пусть . 2.2.1. Пусть лежит на . 2.2.2. Пусть . 2.2.3. Пусть лежит на . 2.3. Пусть (рис. 7.9). 2.3.1. Пусть цепи и имеют более одной общей точки. 2.3.2. Пусть цепи и имеют точно одну общую точку . | ||||||||||||||||||||||||||||||||
Литература
- Асанов М., Баранский В., Расин В. — Дискретная математика — Графы, матроиды, алгоритмы