Реализация запроса в дереве отрезков сверху

Описание

Данная рекурсивная операция позволяет выполнять запросы на дереве отрезков, причем алгоритм запускается от корня и рекурсивно идет сверху вниз.

Алгоритм

Рассмотрим данный алгоритм на примере задачи RSQ(запрос суммы на отрезке), то есть пусть есть уже построенное дерево отрезков и задача найти сумму на отрезке [math][a .. b][/math].

Пример дерева отрезков для вычисления сумм

Будем передавать в качестве параметров рекурсий следующие переменные:

• [math]ver[/math] — номер(в массиве с деревом отрезков) текущей вершины дерева.
• [math]l[/math], [math]r[/math] — левая и правая границы отрезков, за которые "отвечает" наша вершина.
• [math]a[/math], [math]b[/math] — левая и правая границы запрашиваемого отрезка.

Запустим рекурсивную процедуру от всего отрезка(то есть от корневой вершины).

Для текущего состояния проверяем следующие условия :

• Если текущий отрезок не пересекается с искомым, то возвращаем нулевое значение.

Например: текущий [math][1..2][/math], а искомый [math][3 .. 4][/math];

• Текущий отрезок совпадает, то возвращаем значение в текущей вершине.

Например: текущий и искомый [math][2..3][/math];

• Иначе переходим к рекурсивным вызовам функций от детей вершины. При этом сумма на текущем отрезке равна сумме результатов функций, запущенных от детей.

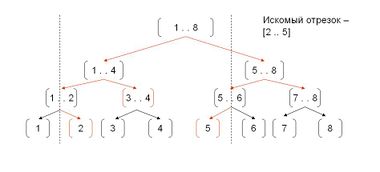
Пример

Дерево отрезков

Рассмотрим работу программы на дереве отрезков для элементов [math][1 .. 8][/math]. Пусть запрашиваемая сумма - это отрезок [math][2 .. 5][/math].

• Текущий отрезок [math][1 .. 8][/math], он больше [math][2 .. 5][/math] => переходим по рекурсивным вызовам на [math][1 .. 4][/math] и [math][5 .. 8][/math]

• [math][1 .. 4][/math] выходит за границы[math] [2 .. 5][/math], [math][5 .. 8][/math] выходит за границы [math][2 .. 5][/math] => переходим по рекурсивным вызовам на [math][1 .. 2][/math], [math][3 .. 4][/math] и [math][5 .. 6][/math], [math][7 .. 8][/math].

• [math][1 .. 2][/math] выходит за границы [math][2 .. 5][/math] => переходим в листья 1, 2; [math][3 .. 4][/math] целиком внутри [math][2 .. 5][/math] => возвращаем значение в [math][3 .. 4][/math];

[math][7 .. 8][/math] не пересекается с [math][2 .. 5][/math] => возвращаем нулевое значение, [math][5 .. 6][/math] выходит за границы [math][2 .. 5][/math] => переходим к листьям 5 и 6

• лист 6 не пересекается с отрезком [math][2 .. 5][/math] => возвращаем нулевое значение, лист 5 целиков внутри [math][2 .. 5][/math] => возвращаем значение в листе 5.

Реализация

 int get_sum (int ver, int l, int r, int a, int b)
 {
       if ([l,r] [math]\bigcap[/math] [a, b] = [math] \varnothing[/math])
           return 0;
       if ([l,r] = [a, b])
           return tree[ver];
       int m = (l + r) / 2;
       return get_sum (ver * 2, l, m, a, min(b, m))
           + get_sum (ver * 2 + 1, m + 1, r, max(a, m + 1), b);
 } 

Ссылки

- MAXimal :: algo :: Дерево отрезков

- Дерево отрезков — Википедия

- Визуализатор дерева отрезков