СНМ (списки с весовой эвристикой)

Определение

Определение:

Весовая эвристика (weighted-union heuristic) — улучшение наивной реализации СНМ, при котором список включает поле длины списка, и добавление идет всегда меньшего списка к большему.

Проблема наивной реализации

Реализация без весовой эвристики

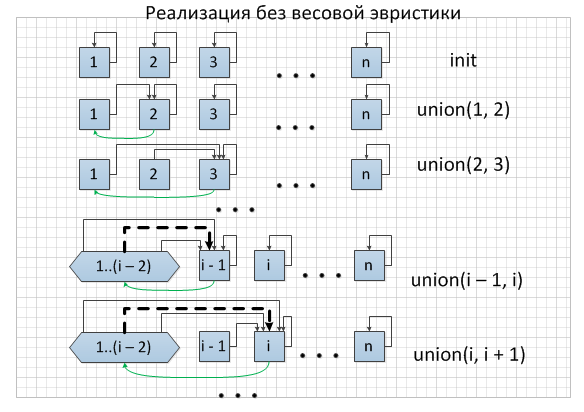
Рассмотрим реализацию системы непересекающихся множеств с помощью списка, для каждого элемента которого будем хранить указатель на представителя и на следующий элемент. При такой реализации операция init для создания n множеств из одного элемента очевидно займет [math]O(n)[/math] времени. Для выполнения операции findSet достаточно просто перейти по ссылке на представителя за [math]O(1)[/math]. Узким местом такой реализации является операция union. Хотя мы и можем объединить два списка за [math]O(1)[/math], но обновить указатели на представителя для одного из списков мы можем лишь за время пропорциональное количеству элементов. Нетрудно придумать последовательность из n - 1 операций union, требующую [math]O(n^2)[/math] времени. Достаточно каждый раз сливать одно и тоже множество с одним новым элементом в том порядке, чтобы требовалось обновить указатели на представителя именно элементам "большого" множества. Поскольку i-ая операция union обновляет i указателей, общее количество указателей, обновленных всеми n - 1 операциями union равно [math]\sum\limits_{i=1}^{n-1} i = O(n^2)[/math]. Отсюда следует, что амортизированное время выполнения операции union составляет [math]O(n)[/math].

Реализация с весовой эвристикой

Очевидным минусом наивной реализации являлось то, что при слиянии двух множеств, например относительно большого и из одного элемента, мы пытались обновить указатели для большого числа элементов, хотя гораздо быстрее было бы поменять указатель лишь одному. Отсюда следуют очевидная оптимизация - давайте будем для каждого множества хранить его размер и изменять указатели на представителя всегда элементам из "меньшего" списка. Эта оптимизация называется весовой эвристикой и позволяет добиться асимптотики [math]O(n \log n)[/math] для n - операций union. Хотя одна операция union по-прежнему может потребовать [math]\Omega(n)[/math] действий, если оба множества имеют [math]\Omega(n)[/math] членов.

Доказательство оценки времени выполнения

Утверждение:

При использовании связанных списков для представления СНМ и применении весовой эвристики, последовательность из m операций makeSet, union, и findSet, n из которых составляют операции makeSet, требует для выполнения [math]O(m+n \log n)[/math] времени.

[math]\triangleright[/math]

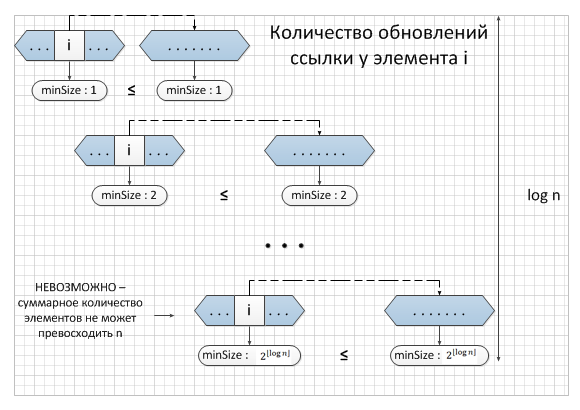
Оценка количества переподвешиваний Вычислим верхнюю границу количества обновлений указателя на представителя для каждого элемента. Рассмотрим некий фиксированный объект. Когда мы обновляем указатель на представителя в элементе, он должен находиться в меньшем из множеств. Следовательно, при первом обновлении образованное множество хранит не менее 2 элементов, при втором не менее 4 элементов, и т.д. Продолжая рассуждение приходим к выводу о том, что при k [math]\leqslant\[/math] n, после того как указатель на представителя в объекте обновлен [math]\left\lceil \log k \right\rceil[/math], полученное в результате множество должно иметь не менее k элементов. Поскольку максимальное множество может иметь не более n элементов, во всех операциях union указатель на представителя у каждого объекта может быть обновлен не более [math]\left\lceil \log n \right\rceil[/math] раз. Таким образом, общее время, необходимое для обновления n объектов, составляет [math]O(n \log n)[/math]. Необходимо также отметить, что слить два списка и обновить поле длинны при выполнении union можно легко за [math]O(1)[/math]. Отсюда легко понять, что время необходимое для выполнения всей последовательности из m операций составит [math]O(m + n \log n)[/math]. [math]O(m)[/math] операций makeSet, findSet и часть работы операции union на обновление поля длины и слияния списков, каждая из которых выполняется за константное время и суммарное время работы операций union для каждого объекта.

[math]\triangleleft[/math]

Другие реализации

• СНМ(наивные реализации)
• СНМ(реализация с помощью леса корневых деревьев)

Источники

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 585—588. — ISBN 5-8489-0857-4

Ссылки

• habrahabr.ru - Система непересекающихся множеств и её применения