Суффиксный бор

Суффиксный бор для строки [math]abbc[/math]

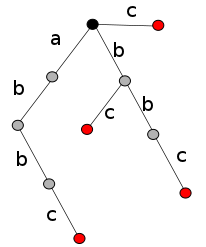
Суффиксный бор (англ. suffix trie) — бор, содержащий все суффиксы данной строки.

По определению, в суффиксном боре для строки [math]s[/math] (где [math]\lvert s\rvert=n[/math]) содержатся все строки [math]s[1..n], ..., s[n..n][/math]. Заметим, что если в суффиксном боре находится строка [math]s[i..n][/math], то все ее префиксы [math]s[i..j], i \le j \le n[/math] уже содержатся в боре.

Применение

Суффиксный бор можно использовать для поиска подстроки в строке [math]s[/math] (чтобы бор формально содержал все подстроки [math]s[/math], нужно пометить все его вершины терминальными, при этом корень будет соответствовать пустой строке [math]\varepsilon[/math]). Для поиска подстроки p в суффиксном боре нужно искать совпадения для символов из p вдоль единственного пути в боре до тех пор, пока либо p не исчерпается, либо дальнейшее совпадение будет невозможным. Если p исчерпалось, то подстрока найдена за [math]O(|p|)[/math], если дальнейшее совпадение невозможно, то p нет в суффиксном дереве.

Свойства

Суффиксный бор для строки [math]s[/math]:

• Можно использовать для поиска образца [math]p[/math] в строке [math]s[/math] за время [math]O(\lvert p\rvert)[/math].
• Можно построить за время [math]O(n^2)[/math], последовательно добавив все суффиксы [math]s[/math].
• Имеет порядка [math]n^2[/math] вершин.

Реализация

struct Trie
   map<char, integer>[length^2] trie 
   number [math] \leftarrow 1[/math]

Add(i, j)
  current [math]\leftarrow[/math] 0 
  for (char c [math]\in[/math] s[i, j])
    if (trie[current] constainKey(c))
      trie[current].add(c, number)  
      number++; 
    current [math]\leftarrow[/math] trie[current][c]

Build(String  s)
  for(int i = 0, i < n, i++)
    Add(i, n)

Оценки использования памяти

Пусть мы построили суффиксный бор для строки [math]s \in \Sigma*[/math], [math]|s| = n[/math]. Из третьего свойства следует, что если хранить переходы суффиксного бора из каждой вершины как массив размера [math]|\Sigma|[/math] (по каждому символу — ребенок), то потребуется [math]O(n^2 |\Sigma|)[/math] памяти. Однако, заметим, что число ветвлений в боре равно количеству суффиксов, так как каждый лист соответствует единственному суффиксу. Количество суффиксов — [math]n[/math], а значит число вершин, из которых ведет больше одного перехода, [math]O(n)[/math]. Поэтому, если в неветвящихся вершинах хранить только символ перехода и ребенка, то можно получить оценку [math]O(n^2 + n|\Sigma|)[/math]. Улучшением суффиксного бора, расходующим всего [math]O( n|\Sigma|)[/math] памяти, является сжатое суффиксное дерево.