Реализация запроса в дереве отрезков снизу — различия между версиями
(→Псевдокод) |
|||
| Строка 5: | Строка 5: | ||
Реализация запроса снизу вверх в дереве отрезков является, в отличие от [[Реализация запроса в дереве отрезков сверху| реализации запроса сверху вниз]], итеративным методом. Будем рассматривать абстрактную операцию, обладающую свойством ассоциативности. | Реализация запроса снизу вверх в дереве отрезков является, в отличие от [[Реализация запроса в дереве отрезков сверху| реализации запроса сверху вниз]], итеративным методом. Будем рассматривать абстрактную операцию, обладающую свойством ассоциативности. | ||
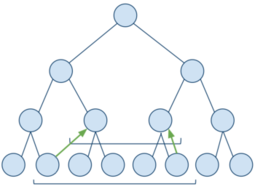
| − | [[Дерево отрезков. Построение|Построим дерево отрезков]] и установим границы отрезка на соответствующие листья. Если элемент, попавший на левую границу, является правым сыном, то запишем в результат значение, полученное после выполнения нашей операции над предыдущим результатом и значением этого элемента, а левую границу перемещаем на один элемент вправо. Аналогично действуем с элементом попавшим на правую границу (является ли этот элемент левым сыном). Затем устанавливаем границы отрезка на родительские элементы текущих границ. Продолжаем до тех пор, пока границы не пересекутся. | + | [[Дерево отрезков. Построение|Построим дерево отрезков]] и установим границы отрезка на соответствующие листья. Если элемент, попавший на левую границу, является правым сыном, то запишем в результат значение, полученное после выполнения нашей операции над предыдущим результатом и значением этого элемента, а левую границу перемещаем на один элемент вправо. Таким образом мы учтем вклад нужной нам вершины и избавимся от вклада ненужного нам поддерева. Аналогично действуем с элементом попавшим на правую границу (является ли этот элемент левым сыном). Затем устанавливаем границы отрезка на родительские элементы текущих границ. Это позволит узнать, входит ли полученный отрезок в искомый или нет. Продолжаем до тех пор, пока границы не пересекутся. Если после завершения цикла границы совпадут, значит полученный отрезок входит в искомый, и надо пересчитать результат, иначе {{---}} ничего делать не надо. |
==Псевдокод== | ==Псевдокод== | ||
Версия 13:43, 3 июня 2012
Алгоритм
Реализация запроса снизу вверх в дереве отрезков является, в отличие от реализации запроса сверху вниз, итеративным методом. Будем рассматривать абстрактную операцию, обладающую свойством ассоциативности.
Построим дерево отрезков и установим границы отрезка на соответствующие листья. Если элемент, попавший на левую границу, является правым сыном, то запишем в результат значение, полученное после выполнения нашей операции над предыдущим результатом и значением этого элемента, а левую границу перемещаем на один элемент вправо. Таким образом мы учтем вклад нужной нам вершины и избавимся от вклада ненужного нам поддерева. Аналогично действуем с элементом попавшим на правую границу (является ли этот элемент левым сыном). Затем устанавливаем границы отрезка на родительские элементы текущих границ. Это позволит узнать, входит ли полученный отрезок в искомый или нет. Продолжаем до тех пор, пока границы не пересекутся. Если после завершения цикла границы совпадут, значит полученный отрезок входит в искомый, и надо пересчитать результат, иначе — ничего делать не надо.
Псевдокод
Пусть ассоциативная операция, над которой построено дерево отрезков, обозначается a b, а результат считаем на отрезке [left, right].
query(left, right)
result = neutral; // Присваиваем результату значение нейтрального элемента (например для поиска суммы надо присвоить значение 0)
while left < right // Выполняем цикл до тех пор, пока левая и правая граница не пересекутся
if (left div 2) * 2 == left // Проверяем, является ли левая граница правым сыном (индексация с 0)
result = result data[left]; // Если является, то пересчитаем результат и перенесем левую границу
left = (left + 1) div 2;
else
left = left div 2; // Если не является, то установим границу на родительский элемент текущей границы
if (right div 2) * 2 + 1 == right // Аналогично проделываем операции с правой границей
result = result data[right];
right = (right - 1) div 2;
else
right = right div 2;
if left == right // После окончания цикла проверяем совпали ли границы
result = result data[left]; // Если надо пересчитываем результат
return result;