Сжатое суффиксное дерево

Суффиксный бор — удобная структура данных для поиска подстроки в строке, но она занимает много места в памяти. Рассмотрим в боре все пути от [math]u[/math] до [math]v[/math], в которых у каждой вершины только один сын. Такой путь можно сжать до ребра [math]u v[/math], записав на нем все встречающиеся на пути символы, которые являются подстрокой исходной строки. Для хранения ее на ребре обычно используют индексы [math]l, r[/math] начала и конца. Получилось сжатое суффиксное дерево.

Определение

Определение:

Суффиксное дерево (сжатое суффиксное дерево) [math]T[/math] для строки [math]s[/math] (где [math]|s| = n[/math]) — дерево с [math]n[/math] листьями, обладающее следующими свойствами: Каждая внутренняя вершина дерева имеет не меньше двух детей; Каждое ребро помечено непустой подстрокой строки [math]s[/math]; Никаких два ребра, выходящие из одной вершины, не могут иметь пометок, начинающихся с одного и того же символа; Дерево должно содержать все суффиксы строки [math]s[/math], причем каждый суффикс заканчивается точно в листе и нигде кроме него.

Суффиксное дерево для строки [math]xabxa[/math] с защитным символом

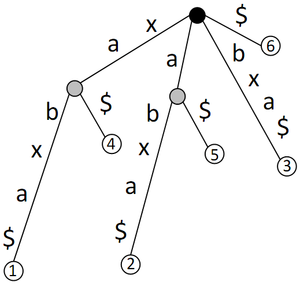
Рассмотрим дерево для строки [math]xabxa[/math]. У него суффикс [math]xa[/math] является префиксом суффикса [math]xabxa[/math], значит, этот суффикс не закачивается в листе. Для решения проблемы в конце строки [math]s[/math] добавляют символ, не входящий в исходный алфавит: защитный символ. Как правило, это [math]\$[/math]. Любой суффикс строки с защитным символом действительно заканчивается в листе и только в листе.

Далее [math]n[/math] - длина строки [math]s[/math] с защитным символом.

Количество вершин

По определению, в суффиксном дереве содержится [math]n[/math] листьев. Рассмотрим количество внутренних вершин такого дерева.

Лемма:

Количество внутренних вершин дерева, каждая из которых имеет не менее двух детей, меньше количества листьев.

Доказательство:

[math]\triangleright[/math]

Докажем лемму индукцией по количеству листьев [math]n[/math]. База При [math]n = 2[/math] в дереве одна внутренняя вершина - верно. Переход [math]n \rightarrow n + 1[/math] Возьмем вершину в дереве с [math]n + 1[/math] листами, у которой два ребенка - листья. Рассмотрим возможные случаи: 1) У нее более двух детей. Тогда отрежем от нее лист. Получим дерево с [math]n[/math] листьями, причем в нем количество внутренних вершин такое же, как в исходном дереве. Но у полученного дерева по индукционному предположению менее [math]n[/math] внутренних вершин, значит, для исходного дерева лемма верна. 2) У нее ровно два ребенка. Отрежем их, получим дерево с [math]n[/math] листьями, количество внутренних вершин которого на [math]1[/math] меньше, чем в исходном дереве. Тогда по индукционному предположению у него менее [math]n[/math] внутренних вершин, значит, в исходном дереве их меньше [math]n + 1[/math].

[math]\triangleleft[/math]

Занимаемая память

Представим дерево как массив [math][|V|*|\Sigma|][/math], где [math]|V|[/math] — количество вершин в дереве, [math]|\Sigma|[/math] - мощность алфавита. Для любого суффиксного дерева верна предыдущая лемма (у каждой вершины по определению не менее двух детей), значит, [math]|V| = O(2*n)[/math]. Каждая [math][i][j][/math] ячейка содержит информацию о том, в какую вершину ведет [math]i-[/math]ое ребро по [math]j-[/math]ому символу и индексы [math]l, r[/math]. Итак, дерево занимает [math]O(n*|\Sigma|)[/math] памяти.

Построение суффиксного дерева

Рассмотрим наивный алгоритм построения суффиксного дерева:

[math]count \leftarrow 0[/math] //номер последней вершины, созданной в дереве (глобальная переменная)
for [math] i \leftarrow 0 [/math] to [math] n [/math] do //для каждого символа строки
    insert([math]i, n[/math]) //добавляем суффикс, начинающийся с него

insert(l, r)
    [math] cur \leftarrow root [/math]
    while ([math] l \lt  r [/math])
         if [math] go[cur][s[l]].v = 0 [/math] //если мы не можем пойти из вершины по символу [math] l [/math]
              createVertex([math]cur, l, r[/math]) //создаем новую вершину 
         else
              [math]start \leftarrow go[cur][s[l]].l [/math]
              [math]finish \leftarrow go[cur][s[l]].r [/math]
              [math]hasBreak \leftarrow false [/math]
              for [math] j = start [/math] to [math] finish [/math] //для каждого символа на ребре из текущей вершины
                   if [math]s[l+j-start] \lt \gt s[j] [/math] //если нашли не совпадающий символ
                        newEdge([math]cur[/math]) //создаем вершину на ребре
                        [math]hasBreak \leftarrow true [/math]
                        break
              if [math]!hasBreak[/math]
                   [math]cur \leftarrow go[cur][s[l]].v [/math] //переходим по ребру
                   [math]l \leftarrow l + finish - start [/math] //двигаемся по суффиксу на длину подстроки, записанной на ребре

createVertex([math]cur, l, r[/math])
    [math]go[cur][s[l]] \leftarrow new Vertex()[/math]
    [math]go[cur][s[l]].v \leftarrow count[/math]
    [math]go[cur][s[l]].l \leftarrow l[/math]
    [math]go[cur][s[l]].r \leftarrow r[/math]
    [math]count++[/math]

newEdge([math]cur[/math])
    [math]next \leftarrow go[cur][s[l]].v[/math]
    createVertex([math]cur, l, j - 1[/math])
    [math]cur \leftarrow go[cur][s[l]].v[/math]
    createVertex([math]cur, j, r[/math])
    [math]go[cur][s[j]].v \leftarrow next [/math]
    [math]go[cur][s[j]].l \leftarrow j [/math]
    [math]go[cur][s[j]].r \leftarrow r [/math]

Этот алгоритм работает за время [math]O(n^2)[/math], однако алгоритм Укконена позволяет построить сжатое суффиксное дерево за [math]O(n)[/math].

Использование сжатого суффиксного дерева

Суффиксное дерево позволяет за линейное время найти:

• Количество различных подстрок данной строки
• Наибольшую общую подстроку двух строк
• Суффиксный массив и массив [math]lcp[/math] (longest common prefix) исходной строки

Источники

• Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.

См. также

• Суффиксный бор
• Суффиксный массив
• Алгоритм Укконена