Интерактивные протоколы. Класс IP. Класс AM — различия между версиями
| Строка 23: | Строка 23: | ||
# <tex> \forall x \in L \Rightarrow P(V(x) = 1) \ge \frac{2}{3} </tex>;<br/> | # <tex> \forall x \in L \Rightarrow P(V(x) = 1) \ge \frac{2}{3} </tex>;<br/> | ||
# <tex> \forall x \notin L \Rightarrow P(V(x) = 1) \le \frac{1}{3} </tex>;<br/> | # <tex> \forall x \notin L \Rightarrow P(V(x) = 1) \le \frac{1}{3} </tex>;<br/> | ||
| − | # число раундов интерактивного протокола <tex> O(f(n)), n = |x|\}</tex><br/> | + | # число раундов интерактивного протокола <tex> O(f(n)), n = |x|\}</tex>.<br/> |
}} | }} | ||
| Строка 33: | Строка 33: | ||
# <tex> \forall x \in L \Rightarrow P(V(x) = 1) \ge \frac{2}{3} </tex>;<br/> | # <tex> \forall x \in L \Rightarrow P(V(x) = 1) \ge \frac{2}{3} </tex>;<br/> | ||
# <tex> \forall x \notin L \Rightarrow P(V(x) = 1) \le \frac{1}{3} </tex>;<br/> | # <tex> \forall x \notin L \Rightarrow P(V(x) = 1) \le \frac{1}{3} </tex>;<br/> | ||
| − | # число раундов интерактивного протокола <tex> O(f(n)), n = |x|\} </tex><br/> | + | # число раундов интерактивного протокола <tex> O(f(n)), n = |x|\} </tex>.<br/> |
}} | }} | ||
| Строка 50: | Строка 50: | ||
{{Теорема | {{Теорема | ||
| − | |statement=<tex>\mathrm{BPP} \subset \mathrm{IP[0]}</tex> | + | |statement=<tex>\mathrm{BPP} \subset \mathrm{IP[0]}</tex>. |
|proof= | |proof= | ||
<tex>V</tex> сам по себе является вероятностной машиной Тьюринга и поэтому может разрешить язык из <tex>\mathrm{BPP}</tex> не прибегая к общению с <tex>P</tex>. | <tex>V</tex> сам по себе является вероятностной машиной Тьюринга и поэтому может разрешить язык из <tex>\mathrm{BPP}</tex> не прибегая к общению с <tex>P</tex>. | ||
| Строка 56: | Строка 56: | ||
{{Теорема | {{Теорема | ||
| − | |statement=<tex>\mathrm{NP} \subset \mathrm{IP[1]}</tex> | + | |statement=<tex>\mathrm{NP} \subset \mathrm{IP[1]}</tex>. |
|proof= | |proof= | ||
Для разрешения языка из <tex>\mathrm{NP}</tex> будем использовать следующий протокол: | Для разрешения языка из <tex>\mathrm{NP}</tex> будем использовать следующий протокол: | ||
| Строка 65: | Строка 65: | ||
|definition= | |definition= | ||
<tex>\mathrm{GNI}</tex> расшифровывается как Graph Non Isomorphism. Это язык пар неизоморфных друг другу графов. | <tex>\mathrm{GNI}</tex> расшифровывается как Graph Non Isomorphism. Это язык пар неизоморфных друг другу графов. | ||
| − | <tex>\mathrm{GNI}=\{ \langle G, H \rangle, </tex> графы <tex>G</tex> и <tex>H</tex> не изоморфны <tex>\}</tex> | + | <tex>\mathrm{GNI}=\{ \langle G, H \rangle, </tex> графы <tex>G</tex> и <tex>H</tex> не изоморфны <tex>\}</tex>. |
}} | }} | ||
{{Теорема | {{Теорема | ||
| − | |statement=<tex>\mathrm{GNI} \in \mathrm{IP[1]}</tex> | + | |statement=<tex>\mathrm{GNI} \in \mathrm{IP[1]}</tex>. |
|proof= | |proof= | ||
Будем использовать следующий алгоритм для <tex>V</tex>: | Будем использовать следующий алгоритм для <tex>V</tex>: | ||
Версия 01:36, 4 июня 2012
Класс IP
| Определение: |
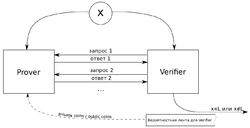
Интерактивным протоколом, разрешающим язык , называется абстрактная машина (см. рис. 1), моделирующая вычисления как обмен сообщениями между двумя программами (Prover и Verifier, далее и соответственно), такими, что
|
Интерактивные протоколы делятся на два типа в зависимости от доступа к вероятностной ленте :
- public coins — может видеть вероятностную ленту ;
- private coins — не может видеть вероятностную ленту .
| Определение: |
|
Язык \mathrm{AM} (Arthur–Merlin games) отличается от \mathrm{IP} лишь тем, что может видеть вероятностную ленту .
| Определение: |
|
| Определение: |
| Если для интерактивного протокола выполняется , то говорят, что он обладает свойством completeness . |
| Определение: |
| Если для интерактивного протокола выполняется , то говорят, что он обладает свойством soundness . |
Свойство completeness можно достичь, а soundness достичь нельзя.
| Теорема: |
. |
| Доказательство: |
| сам по себе является вероятностной машиной Тьюринга и поэтому может разрешить язык из не прибегая к общению с . |
| Теорема: |
. |
| Доказательство: |
|
Для разрешения языка из будем использовать следующий протокол: будет проверять на принадлежность слова используя сертификат, который он запросит у . Так как не ограничен в вычислительной мощности, он может подобрать подходящий сертификат и именно его и сообщит, так как он заинтересован в том, чтобы принял слово. Для этого требуется лишь один раунд интерактивного протокола. |
| Определение: |
| расшифровывается как Graph Non Isomorphism. Это язык пар неизоморфных друг другу графов. графы и не изоморфны . |
| Теорема: |
. |
| Доказательство: |
|
Будем использовать следующий алгоритм для :
Покажем, что это удовлетворяет ограничениям на .
Во-первых, очевидно, что число раундов не превосходит двух.
|