Ортогональный поиск

Эта статья находится в разработке!

Простейший случай

Пусть дана прямая с точками на ней и отрезок. Точки даны в отсортированном порядке. Необходимо указать, какие из изначальных точек лежат на этом отрезке.

Данная задача решается с помощью функций из STL - upper_bound и lower_bound.

lower_bound возвращает итератор на первый элемент, больший либо равный данного.
upper_bound возвращает итератор на первый элемент множества со значением, большим данного.

Рассмотрим на примере:

Код реализации:

template<class RauIter, class OutIter, class Scalar> OutIter range_search(RauIter p, RauIter q, OutIter out)
{
   return std::copy(lower_bound(p, q, l), upper_bound(p, q, r), out);
}

Сбалансированное дерево поиска

Переходим к двумерному случаю. Пусть дано некоторое множество точек на плоскости. Нам необходимо ответить, какие именно из них лежат в некотором заданном прямоугольнике.

Для этого возьмем любое сбалансированное дерево поиска и наполним его точками [math](x, y)[/math] из множества. В качестве ключа будет использоваться [math]x[/math]-координата точки. Теперь модернизируем дерево: в каждой вершине дерева будем хранить отсортированный по [math]y[/math]-координате массив точек, которые содержатся в соответствующем поддереве.
Рассмотрим на примере:

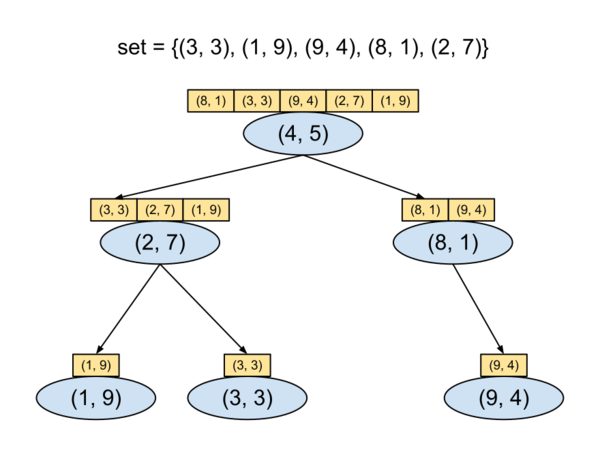
Рассмотрим, как в такой структуре данных будет выглядеть поиск множества точек, находящихся в заданном прямоугольнике [math](x_{min}, x_{max}) \times (y_{min}, y_{max})[/math]. Для начала, найдем в дереве те точки, [math]x[/math]-координата которых лежит в интервале [math](x_{min}, x_{max})[/math]. Сделаем это следующим образом:

1. Найдем в дереве поиска вершины с минимальной и максимальной [math]x[/math]-координатой из прямоугольника запроса, добавим их в искомое множество, обозначим их как [math]v_l[/math] и [math]v_r[/math].
2. Добавим в искомое множество их наименьшего общего предка [math]v_n[/math].
3. Для каждой из промежуточных вершин [math]v_i[/math] на восходящем пути [math]v_l \to v_n[/math] зафиксируем, из какого ребенка мы поднялись в вершину [math]v_i[/math]. Если мы поднялись из левого сына, то добавим в искомое множество саму вершину [math]v_i[/math], а также множество точек, находящихся в поддереве правого сына вершины [math]v_i[/math]. Если же мы поднялись из правого сына, то не добавляем ничего.
4. Повторим процесс для пути [math]v_r \to v_n[/math]. Здесь ориентация сторон инвертирована: будем пополнять множество в том случае, если мы поднялись из правого сына.

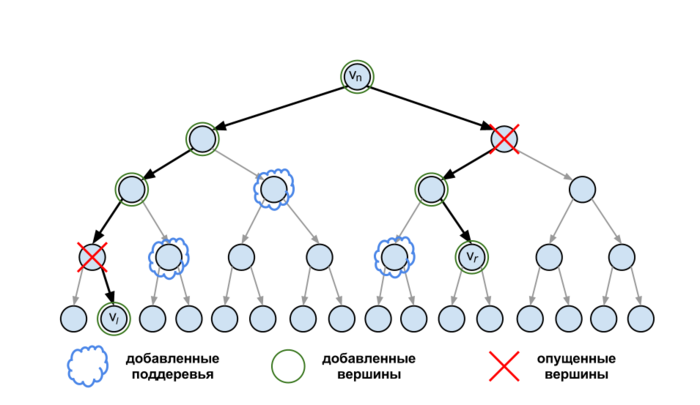
В итоге, в множество мы добавим [math]O(\log n)[/math] вершин и [math]O(\log n)[/math] поддеревьев дерева поиска. Теперь нужно просеять полученное множество — извлечь из него те элементы, [math]y[/math]-координата которых не лежит в интервале [math](y_{min}, y_{max})[/math]. Для точек это сделать просто — нужно вручную проверить, лежит ли [math]y[/math]-координата в нужном интервале. Для каждого из полученных поддеревьев обратимся к массиву содержащихся в нем точек и запустим от него приведенную выше функцию [math]range{\_}search(y_{min}, y_{max})[/math]. Все полученные таким образом точки и будут составлять ответ.
Каждая из функций [math]range{\_}search(y_{min}, y_{max})[/math] будет работать в худшем случае за [math]O(\log n)[/math], отсюда получаем итоговое время выполнения запроса [math]O(\log^2 n)[/math]. Что касается памяти, то в сбалансированном дереве поиска [math]O(\log n)[/math] слоев, а каждый слой хранит массивы, содержащие в сумме ровно [math]n[/math] точек, соответственно вся структура в целом занимает [math]O(n\log n)[/math] памяти.

Такую структуру данных можно при необходимости обобщить на случай большей размерности. Пусть у нас есть множество точек из [math]p[/math]-мерного пространства, каждая из которых представляется как [math]n[/math] координатных чисел: [math](\xi_1, \xi_2, ... , \xi_p)[/math]. Тогда, строя дерево поиска по координате [math]\xi_i[/math], в каждой вершине будем хранить другое дерево поиска с ключом [math]\xi_{i+1}[/math], составленное из точек, лежащих в соответствующем поддереве. В дереве поиска, составленном по предпоследней координате [math]\xi_{p-1}[/math], уже не будет необходимости хранить в каждой вершине целое дерево, поскольку при переходе на последнюю координату [math]\xi_{p}[/math] дальнейший поиск производиться не будет, поэтому в вершинах будем хранить массивы, так же, как и в двумерном случае. Оценим занимаемую память и время запроса: при добавлении следующей координаты асимптотика обеих величин умножается на [math]\log n[/math]. Отсюда, получаем оценку [math]O(\log^{p} n)[/math] на время запроса и [math]O(n\log^{p-1} n)[/math] на занимаемую память.

Такой же результат можно получить с помощью сжатого многомерного дерева отрезков.

Прошитые отсортированные массивы

Для ускорения запроса можно "прошить" дерево поиска, а именно: каждый элемент массива, сохраненного в какой-либо вершине, соединить с элементами массивов, сохраненных в вершинах-детях. Соединять будем по следующему принципу: элемент [math](x, y)[/math] массива-предка соединим с элементами [math]upper\_bound(y)[/math] и [math]lower\_bound(y)[/math] каждого массива-ребенка. Тогда для выполнения завершающей фазы поиска нам достаточно будет посчитать [math]upper\_bound()[/math] и [math]lower\_bound()[/math] только на массиве, привязанному к корню дерева. Для получения границ на других массивах можно будет просто спуститься по ссылкам от массива-предка за [math]O(1)[/math]. Таким образом, поиск теперь будет выполняться за [math]O(\log^{p-1} n)[/math], где [math]p[/math] — размерность пространства.

TODO: здесь тоже надо что-нибудь нарисовать