Биномиальная куча

Пример биномиальных деревьев [math]B_0, B_2, B_3[/math]

Биномиальное дерево

Определение:

Биномиальное дерево [math]B_k[/math] — дерево, определяемое для каждого [math]k = 0, 1, 2, \dots [/math] следующим образом: [math]B_0[/math] — дерево, состоящее из одного узла; [math]B_k[/math] состоит из двух биномиальных деревьев [math]B_{k-1}[/math], связанны вместе таким образом, что корень одного из них является дочерним узлом корня второго дерева.

Свойства биномиальных деревьев

Утверждение:

Биномиальное дерево [math]B_k[/math] с [math]n[/math] вершинами имеет [math]2^k[/math] узлов

[math]\triangleright[/math]

Докажем по индукции: База [math]k = 1[/math] — верно. Пусть для некоторого [math]k [/math] условие верно, то докажем, что для [math]k + 1[/math] это также верно: Так как в дереве порядка [math]k+1[/math] вдвое больше узлов, чем в дереве порядка [math]k[/math], то дерево порядка [math]k+1[/math] имеет [math]2^k * 2 = 2^{k+1}[/math] узлов. Переход доказан, то биномиальное дерево [math]B_k[/math] с [math]n[/math] вершинами имеет [math]2^k[/math] узлов.

[math]\triangleleft[/math]

Утверждение:

Биномиальное дерево [math]B_k[/math] с [math]n[/math] вершинами имеет высоту [math]k[/math];

[math]\triangleright[/math]

Докажем по индукции: База [math]k = 1[/math] — верно. Пусть для некоторого [math]k [/math] условие верно, то докажем, что для [math]k + 1[/math] это также верно: Так как в дереве порядка [math]k+1[/math] высота больше на [math]1[/math] (так как мы подвешиваем к текущему дереву дерево того же порядка), чем в дереве порядка [math]k[/math], то дерево порядка [math]k+1[/math] имеет высоту [math]k + 1[/math]. Переход доказан, то биномиальное дерево [math]B_k[/math] с [math]n[/math] вершинами имеет высоту [math]k[/math].

[math]\triangleleft[/math]

Утверждение:

Биномиальное дерево [math]B_k[/math] с [math]n[/math] вершинами имеет ровно [math]{k\choose i}[/math] узлов на высоте [math]i[/math];

[math]\triangleright[/math]

Докажем по индукции: База [math]k = 1[/math] — верно. Пусть для некоторого [math]k [/math] условие верно, то докажем, что для [math]k + 1[/math] это также верно: Рассмотрим [math]i[/math] уровень дерева [math]B_{k+1}[/math]. Дерево [math]B_{k+1}[/math] было получено подвешиванием одного дерева порядка [math]k[/math] к другому. Тогда на [math]i[/math] уровне дерева [math]B_{k+1}[/math] всего узлов [math]{k\choose i} + {k\choose {i - 1}}[/math], так как от подвешенного дерева в дерево порядка [math]k+1[/math] нам пришли узлы глубины [math]i-1[/math]. То для [math]i[/math]-го уровня дерева [math]B_{k+1}[/math] количество узлов [math]{k\choose i} + {k\choose {i - 1}} ={{k + 1}\choose i} [/math]. Переход доказан, то биномиальное дерево [math]B_k[/math] с [math]n[/math] вершинами имеет ровно [math]{k\choose i}[/math] узлов на высоте [math]i[/math].

[math]\triangleleft[/math]

Утверждение:

Биномиальное дерево [math]B_k[/math] с [math]n[/math] вершинами имеет корень степени [math]k[/math]; степень всех остальных вершин меньше степени корня биномиального дерева;

[math]\triangleright[/math]

Так как в дереве порядка [math]k+1[/math] степень корня больше на [math]1[/math], чем в дереве порядка [math]k[/math], а в дереве нулевого порядка степень корня [math]0[/math], то дерево порядка [math]k[/math] имеет корень степени [math]k[/math]. И так как при таком увеличении порядка (при переходе от дерева порядка [math]k[/math] к [math]k+1[/math]) в полученном дереве лишь степень корня возрастает, то доказываемый инвариант, то есть степень корня больше степени остальных вершин, не будет нарушаться.

[math]\triangleleft[/math]

Утверждение:

В биномиальном дереве [math]B_k[/math] с [math]n[/math] вершинами максимальная степень произвольного узла равна [math]\log(n)[/math].

[math]\triangleright[/math]

Докажем это утверждение для корня. Степень остальных вершин меньше по предыдущему свойству. Так как степень корня дерева порядка [math]k[/math] равна [math]k[/math], а узлов в этом дереве [math]n = 2^k[/math], то прологарифмировав обе части получаем, что [math]k=O(\log(n))[/math], то степень произвольного узла не более [math]\log(n)[/math].

[math]\triangleleft[/math]

Биномиальная куча

Определение:

Биномиальная куча представляет собой множество биномиальных деревьев, которые удовлетворяют следующим свойствам: Каждое биномиальное дерево в пирамиде подчиняется свойству неубывающей пирамиды: ключ узла не меньше ключа его родительского узла (упорядоченное в соответствии со свойством неубывающей пирамиды дерево). Для любого неотрицательного целого [math]k[/math] найдется не более одного биномиального дерева, чей корень имеет степень [math]k[/math].

Представление биномиальных куч

Поскольку количество детей у узлов варьируется в широких пределах, ссылка на детей осуществляется через левого ребенка, а остальные дети образуют односвязный список. Каждый узел в биномиальной пирамиде (куче) представляется набором полей:

• [math]key[/math] — ключ (вес) элемента;
• [math]parent[/math] — указатель на родителя узла;
• [math]child[/math] — указатель на левого ребенка узла;
• [math]sibling[/math] — указатель на правого брата узла;
• [math]degree[/math] — степень узла (количество дочерних узлов данного узла).

Корни деревьев, их которых состоит пирамида, содержатся в так называемом списке корней, при проходе по которому степени соответствующих корней находятся в возрастающем порядке. Доступ к куче осуществляется ссылкой на первый корень в списке корней.

Операции над биномиальными кучами

Рассмотрим операции, которые можно производить с биномиальной пирамидой. Время работы указано в таблице:

insert	[math]O(\log(n))[/math]
getMinimum	[math]O(\log(n))[/math]
extractMin	[math]\Theta(\log(n))[/math]
merge	[math]\Omega(\log(n))[/math]
decreaseKey	[math]\Theta(\log(n))[/math]
delete	[math]\Theta(\log(n))[/math]

Обозначим нашу кучу за [math]H[/math]. То пусть [math]H.head[/math] — указатель на корень биномиального дерева минимального порядка этой кучи. Изначально [math]H.head = null[/math], то есть пирамида не содержит элементов.

getMinimum

Для нахождения минимального элемента надо найти элемент в списке корней с минимальным значением (предполагается, что ключей, равных [math]\infty[/math], нет).

Так как корней в этом списке не более [math]\lfloor \log(n) \rfloor + 1[/math], то операция выполняется за [math]O(\log(n))[/math].

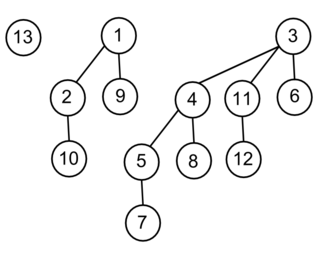
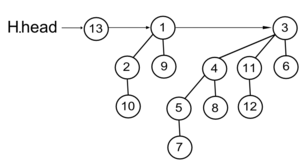
При вызове этой процедуры для кучи, изображенной на картинке ниже, будет возвращен указатель на вершину с ключом [math]1[/math].

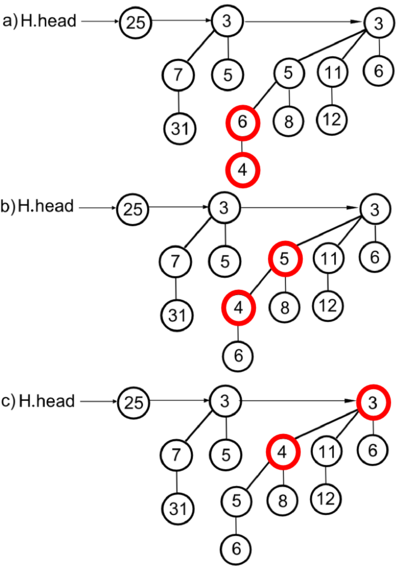
merge

Эта операция, соединяющая две биномиальные кучи в одну, используется в качестве подпрограммы большинством остальных операций.

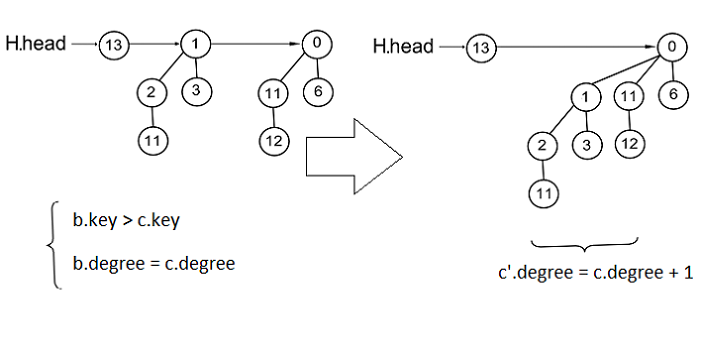
Вот в чем состоит ее суть: пусть есть две биномиальные кучи с [math]H[/math] и [math]H'[/math]. Размеры деревьев в кучах соответствуют двоичным числам [math]m[/math] и [math]n[/math], то есть при наличии дерева соответствующего порядка в этом разряде числа стоит единица, иначе ноль. При сложении столбиком в двоичной системе происходят переносы, которые соответствуют слияниям двух биномиальных деревьев [math]B_{k-1}[/math] в дерево [math]B_{k}[/math]. Надо только посмотреть, в каком из сливаемых деревьев корень меньше, и считать его верхним (пример работы для одного случая приведен на рисунке справа; в другом случае подвешиваем наоборот).

Работа этой процедуры начинается с соединения корневых списков куч в единый список, в котором корневые вершины идут в порядке неубывания их степеней.

В получившемся списке могут встречаться пары соседних вершин одинаковой степени. Поэтому мы начинаем соединять деревья равной степени и делаем это до тех пор, пока деревьев одинаковой степени не останется. Этот процесс соответствует сложению двоичных чисел столбиком, и время его работы пропорционально числу корневых вершин, то есть операция выполняется за [math]\Omega(\log(n))[/math].

Node merge(H1, H2)
   if H1 == null 
      return H2 
    
   if H2 == null 
      return H1 
  
   // H - результат слияния
   H.head = null

   // Слияние корневых списков
   curH = H.head
   curH1 = H1.head
   curH2 = H2.head
   while curH1 != null && curH2 != null 
      if curH1.degree < curH2.degree 
         curH.sibling = curH1
         curH = curH1
         curH1 = curH1.sibling
      else 
         curH.sibling = curH2
         curH = curH2
         curH2 = curH2.sibling

   if curH1 == null 
      while curH2 != null 
         curH.sibling = curH2
         curH2 = curH2.sibling
   else 
      while curH1 != null 
         curH.sibling = curH1
         curH1 = curH1.sibling
     
   // объединение деревьев одной степени
   curH = H.head
   while curH.sibling != null 
      if curH.degree == curH.sibling.degree
         p[curH] = curH.sibling
         tmp = curH.sibling
         curH.sibling = curH.sibling.child
         curH = tmp
         continue
     
      curH = curH.sibling

   return H

insert

Чтобы добавить новый элемент в биномиальную кучу нужно создать биномиальную пирамиду [math]H'[/math] с единственным узлом, содержащим этот элемент, за время [math]O(1)[/math] и объединить ее с биномиальной пирамидой [math]H[/math] за [math]O(\log(n))[/math], так как в данном случае куча [math]H'[/math] содержит лишь одно дерево.

extractMin

Приведенная ниже процедура извлекает узел с минимальным ключом из биномиальной кучи и возвращает указатель на извлеченный узел.

Рассмотрим пошагово алгоритм:

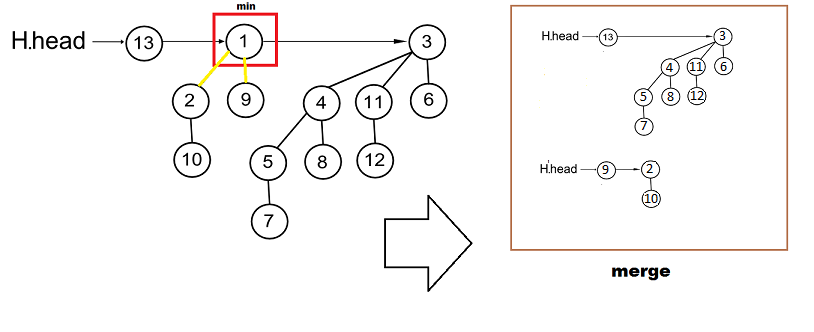
• Найдем биномиальное дерево с минимальным корневым значением. Предположим, что это дерево [math]B_k[/math]. Время работы этого шага алгоритма [math]\Theta(\log n)[/math].
• Удаляем дерево [math]B_k[/math] из кучи [math]H[/math]. Иными словами удаляем его корень из списка корней кучи. Это можно сделать за время [math]O(1)[/math].
• Пусть [math]H'[/math] — куча детей найденного корня. При этом мы для каждого из ребенка устанавливаем указатель на предка равным [math]null[/math]. После этого сливаем кучу [math]H'[/math] c [math]H[/math] за [math]\Omega(\log(n))[/math].

Процедура выполняется за время [math]\Theta(\log(n))[/math], поскольку всего в списке [math]\Theta(\log(n))[/math] корней биномиальных деревьев. И всего у найденного дерева [math] k [/math] порядка (с минимальным значением ключа) ровно [math] k [/math] детей, то сложность перебора этих детей будет тоже [math]\Theta(\log(n))[/math]. А процесс слияния выполняется за [math]\Omega(\log(n))[/math]. Таким образом операция выполняется [math]\Theta(\log(n))[/math].

 Node extractMin(H) {
   //поиск корня х с минимальным значением ключа в списке корней Н:
   min = [math]\infty[/math];
   x = null;
   xBefore = null;

   curx = H.head;
   curxBefore = null;
   while curx != null 
      // релаксируем текущий минимум
      if curx.key < min 
         min = curx.key;
         x = curx; 
         xBefore = curxBefore; 
     
      curxBefore = curx;
      curx = curx.sibling;
   
   //удаление найденного корня x из списка корней деревьев кучи
   if (xBefore == null) 
      H.head = x.sibling;
   else 
      xBefore.sibling = x.sibling;
   

   //построение кучи детей вершины x, при этом изменяем предка соответствующего ребенка на null:
   H' = null;
   curx = x.child;
   H'.head = x.child;
   while curx != null 
      // меняем указатель на родителя узла curx
      p[curx] = null;
      // переход к следующему ребенку
      curx = curx.sibling;
  
   // слияние нашего дерева с деревом H'
   H = merge(H, H'); 
   return x;
 }

decreaseKey

Следующая процедура уменьшает ключ элемента [math]x[/math] биномиальной кучи, присваивая ему новое значение. Вершина, ключ которой был уменьшен, «всплывает» как в обычной куче. Процедура выполняется за время [math]\Theta(\log(n))[/math], поскольку глубина вершины [math]x[/math] в худшем случае есть [math]\Theta(\log(n))[/math] (свойства биномиального дерева), а при выполнении каждого шага алгоритма мы поднимаемся вверх.

 void decreaseKey(H, x, k) { 
  // проверка на то, что текущий ключ не меньше передаваемого ключа k
   if k > key[x]
      return;
   key[x] = k;
   y = x;
   z = p[y];
   //поднимаем текущий элемент x с новым ключом k, пока
   //это значение меньше значения в родительской вершине 
   while z != null and key[y] < key[z]
      swap(key[y], key[z]);
      y = z;
      z = p[y];
 }

Пример работы процедуры проиллюстрирован на рисунке ([math]y[/math] — уменьшаемый элемент, [math]z[/math] — его предок).

delete

Удаление ключа сводится к операциям decreaseKey и extractMin: сначала нужно уменьшить ключ до минимально возможного значения, а затем извлечь вершину с минимальным ключом. В процессе выполнения процедуры этот узел всплывает вверх, откуда и удаляется. Процедура выполняется за время [math]\Theta(\log(n))[/math], поскольку каждая из операций, которые используется в реализаций, работают за [math]\Theta(\log(n))[/math].

 void delete(H, x) {
   //уменшение ключа до минимально вохможного значения
   decreaseKey(H, x, [math]-\infty[/math]);
   //удаление "всплывшего" элемента
   extractMin(H);
 }

Источники

• Биномиальные кучи — INTUIT.ru
• Binomial heap — Wikipedia
• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 538—558. — ISBN 5-8489-0857-4