Сортировка кучей

Сортировка кучей, пирамидальная сортировка (англ. Heapsort) — алгоритм сортировки, использующий структуру данных двоичная куча. Это неустойчивый алгоритм сортировки с временем работы [math]O(n\log{n})[/math] , где [math]n[/math] — количество элементов для сортировки, и использующий [math]O(1)[/math] дополнительной памяти.

Алгоритм

Необходимо отсортировать массив [math]A[/math], размером [math]n[/math]. Построим на базе этого массива за [math]O(n)[/math] невозрастающую кучу. Так как по свойству кучи максимальный элемент находится в корне, то, поменявшись его местами с [math]A[n - 1][/math], он встанет на свое место. Далее вызовем процедуру [math]sift\_down(0)[/math], предварительно уменьшив [math]heap\_size[/math] на [math]1[/math]. Она за [math]O(\log{n})[/math] просеет [math]A[0][/math] на нужное место и сформирует новую кучу (так как мы уменьшили ее размер, то куча располагается с [math]A[0][/math] по [math]A[n - 2][/math], а элемент [math]A[n-1][/math] находится на своем месте). Повторим эту процедуру для новой кучи, только корень будет менять местами не с [math]A[n - 1][/math], а с [math]A[n-2][/math]. Делая аналогичные действия, пока [math]heap\_size[/math] не станет равен [math]1[/math], мы будем ставить наибольшее из оставшихся чисел в конец не отсортированной части. Очевидно, что таким образом, мы получим отсортированный массив.

Реализация

[math]A[/math] — массив, который необходимо отсортировать; [math]n[/math] — количество элементов в нем; [math]build\_heap(A)[/math] - процедура, которая строит из передаваемого массива невозрастающую кучу в этом же массиве; [math]sift\_down(A, i, len)[/math] — процедура, которая просеивает вниз элемент [math]A[i][/math] в куче из [math]len[/math] элементов, находящихся в начале массива [math]A[/math].

heapsort(A)
  build_heap(A);
  heap_size = A.size;
  for i = 0 to n - 2
    swap(A[0], A[n - 1 - i]);
    heap_size--;
    sift_down(A, 0, heap_size);

Сложность

Операция [math]sift\_down[/math] работает за [math]O(\log{n})[/math]. Всего цикл выполняется [math](n - 1)[/math] раз. Таким образом сложность сортировки кучей является [math]O(n\log{n})[/math].

Пример

Строим кучу	Первый проход	Строим новую кучу
Второй проход	Третий проход	Четвертый проход

Пусть дана последовательность из [math]5[/math] элементов [math]3, 2, 4, 1, 5[/math].

Массив	Описание шага
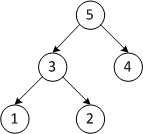
5 3 4 1 2	Строим кучу из исходного массива
Первый проход
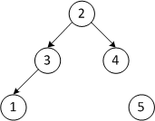
2 3 4 1 5	Меняем местами первый и последний элементы
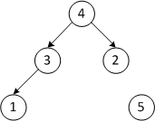
4 3 2 1 5	Строим кучу из первых четырех элементов
Второй проход
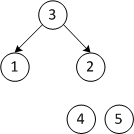
1 3 2 4 5	Меняем местами первый и четвертый элементы
3 1 2 4 5	Строим кучу из первых трех элементов
Третий проход
2 1 3 4 5	Меняем местами первый и третий элементы
2 1 3 4 5	Строим кучу из двух элементов
Четвертый проход
1 2 3 4 5	Меняем местами первый и второй элементы
1 2 3 4 5	Массив отсортирован

JSort

JSort является модификацией сортировки кучей, которую придумал Джейсон Моррисон (Jason Morrison). Если построить на массиве последовательно 2 кучи (невозрастающую и неубывающую), это значительно упорядочит его. Досортировав его сортировкой вставками, можно получить временную сложность [math]O(n)[/math] в лучшем случае.

Алгоритм

Необходимо отсортировать массив. Построим невозрастающую кучу на этом массиве. Тогда наименьший элемент окажется на первой позиции, а левая часть массива окажется почти отсортированной, так как ей будут соответствовать верхние узлы кучи. Теперь построим на этом же массиве кучу так, чтобы немного упорядочить правую часть массива. Эта куча должна быть неубывающей и быть "зеркальной" к массиву, то есть чтобы ее корень соответствовал последнему элементу массива. Получившийся почти отсоротированный массив досортируем сортировкой вставками.

Сложность

Постройка кучи занимает [math]O(n)[/math]. Сортировка вставками может отсортировать массив за [math]O(n)[/math] в лучшем случае, и за [math]O(n^2)[/math] в худшем.

Таким образом временная сложность JSort является [math]O(n^2)[/math].

Ссылки

• Пирамидальная сортировка - Википедия
• Heapsort - Wikipedia
• JSort - Wikipedia
• Описание сортировки кучей и JSort - Хабрахабр

Литература

• Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, 2-е издание. М.: Издательский дом "Вильямс", 2005. ISBN 5-8459-0857-4