Суффиксный бор — различия между версиями
(→Применение) |
(small fixes) |
||
| Строка 30: | Строка 30: | ||
==Оценки использования памяти== | ==Оценки использования памяти== | ||
| − | Пусть мы построили суффиксный бор для строки <tex>s \in \Sigma*</tex>, <tex>|s| = n</tex>. Из третьего свойства следует, что если хранить переходы суффиксного бора из каждой вершины как массив размера <tex>|\Sigma|</tex> (по каждому символу — | + | Пусть мы построили суффиксный бор для строки <tex>s \in \Sigma^*</tex>, <tex>|s| = n</tex>. Из третьего свойства следует, что если хранить переходы суффиксного бора из каждой вершины как массив размера <tex>|\Sigma|</tex> (по каждому символу — переход), то потребуется <tex>O(n^2 |\Sigma|)</tex> памяти. |
| − | Однако, заметим, что число ветвлений в | + | Однако, заметим, что число ветвлений в не превышает числа листьев, что, в свою очередь, не превышает количества суффиксов. Количество суффиксов — <tex>n</tex>, а значит число вершин, из которых ведет больше одного перехода, <tex>O(n)</tex>. Поэтому, если в неветвящихся вершинах хранить только символ перехода и ребенка, то можно получить оценку <tex>O(n^2 + n|\Sigma|)</tex>. Улучшением суффиксного бора, расходующим всего <tex>O( n|\Sigma|)</tex> памяти, является [[сжатое суффиксное дерево]]. |
| + | |||
| + | ==См. также== | ||
| + | * [[Сжатое суффиксное дерево]] | ||
[[Категория:Алгоритмы и структуры данных]] | [[Категория:Алгоритмы и структуры данных]] | ||
[[Категория:Словарные структуры данных]] | [[Категория:Словарные структуры данных]] | ||
Версия 13:02, 12 июня 2012
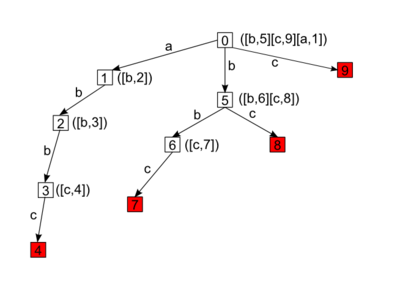
Суффиксный бор (англ. suffix trie) — бор, содержащий все суффиксы данной строки.
По определению, в суффиксном боре для строки (где ) содержатся все строки . Заметим, что если в суффиксном боре находится строка , то все ее префиксы уже содержатся в боре.
Применение
Суффиксный бор можно использовать для поиска подстроки в строке тем же образом, что и для поиска строки в боре. Чтобы бор формально содержал все подстроки , нужно пометить все его вершины терминальными, при этом корень будет соответствовать пустой строке .
Свойства
Суффиксный бор для строки :
- Можно использовать для поиска образца в строке за время .
- Можно построить за время , последовательно добавив все суффиксы .
- Имеет порядка вершин.
Реализация
struct Trie
map<char, integer>[length^2] trie
number
Add(i, j) current 0 for (char c s[i, j]) if (trie[current] constainKey(c)) trie[current].add(c, number) number++; current trie[current][c]
Build(String s)
for(int i = 0, i < n, i++)
Add(i, n)
Оценки использования памяти
Пусть мы построили суффиксный бор для строки , . Из третьего свойства следует, что если хранить переходы суффиксного бора из каждой вершины как массив размера (по каждому символу — переход), то потребуется памяти. Однако, заметим, что число ветвлений в не превышает числа листьев, что, в свою очередь, не превышает количества суффиксов. Количество суффиксов — , а значит число вершин, из которых ведет больше одного перехода, . Поэтому, если в неветвящихся вершинах хранить только символ перехода и ребенка, то можно получить оценку . Улучшением суффиксного бора, расходующим всего памяти, является сжатое суффиксное дерево.