Префикс-функция — различия между версиями
Vasin (обсуждение | вклад) (→Оптимизация) |
Vasin (обсуждение | вклад) (→Оптимизация) |
||
| Строка 38: | Строка 38: | ||
==Оптимизация== | ==Оптимизация== | ||
Вносятся несколько важных замечаний: | Вносятся несколько важных замечаний: | ||
| − | *Следует заметить, что <tex>\pi(i) \le \pi(i-1) + 1</tex>. Действительно, если <tex>\pi(i) > \pi(i-1) + 1</tex>, тогда <tex>\pi(i) - 1 > \pi(i-1)</tex> | + | *Следует заметить, что <tex>\pi(i) \le \pi(i-1) + 1</tex>. Действительно, если <tex>\pi(i) > \pi(i-1) + 1</tex>, тогда <tex>\pi(i) - 1 > \pi(i-1)</tex>. Значит в <tex>\pi(i-1)</tex> не максимально возможное значение, получено противоречие. |
*Нужно избавиться от явных сравнений строк. Пусть вычислено <tex>\pi(i-1)</tex> и <tex>s[\pi(i-1) + 1] = s[i]</tex>, тогда <tex>\pi(i) = \pi(i-1) + 1</tex>. Если <tex>s[\pi(i) + 1] </tex> отличается от <tex>s[i]</tex>, то нужно найти наибольшую длину <tex> k</tex>, для которой верно <tex>\pi(i) = k + 1</tex>. Когда найдется такое <tex>k</tex> достаточно будет сравнить <tex>s[k + 1]</tex> и <tex>s[i]</tex>, при их равенстве <tex>\pi(i) = k + 1</tex> будет верно. Итеративно продолжается поиск <tex>k</tex>, пока оно больше нуля. Если <tex>k=0</tex>, то при <tex>s[i] = s[1]</tex> значение <tex>\pi(i)=1</tex> , иначе нулю. Общая схема алгоритма есть, теперь нужно научиться искать <tex>k</tex>. | *Нужно избавиться от явных сравнений строк. Пусть вычислено <tex>\pi(i-1)</tex> и <tex>s[\pi(i-1) + 1] = s[i]</tex>, тогда <tex>\pi(i) = \pi(i-1) + 1</tex>. Если <tex>s[\pi(i) + 1] </tex> отличается от <tex>s[i]</tex>, то нужно найти наибольшую длину <tex> k</tex>, для которой верно <tex>\pi(i) = k + 1</tex>. Когда найдется такое <tex>k</tex> достаточно будет сравнить <tex>s[k + 1]</tex> и <tex>s[i]</tex>, при их равенстве <tex>\pi(i) = k + 1</tex> будет верно. Итеративно продолжается поиск <tex>k</tex>, пока оно больше нуля. Если <tex>k=0</tex>, то при <tex>s[i] = s[1]</tex> значение <tex>\pi(i)=1</tex> , иначе нулю. Общая схема алгоритма есть, теперь нужно научиться искать <tex>k</tex>. | ||
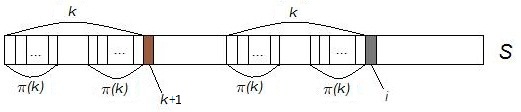
| − | *За исходное <tex>k</tex> нужно взять <tex>\pi(i - 1)</tex>, что следует из первого пункта | + | *За исходное <tex>k</tex> нужно взять <tex>\pi(i - 1)</tex>, что следует из первого пункта. В случае, когда символы <tex>s[k+1]</tex> и <tex>s[i]</tex> не совпадают, <tex>\pi(k)</tex> {{---}} следующая по максимальности длина потенциального наибольшего общего префикса, что видно из рисунка. Последнее утверждение верно, пока <tex>k>0</tex>, что позволит всегда найти его следующее значение. |
[[Файл:Prefix2.jpg]] | [[Файл:Prefix2.jpg]] | ||
Версия 14:32, 12 июня 2012
Префикс-функция строки — функция .
Содержание
Алгоритм
Наивный алгоритм вычисляет префикс функцию непосредственно по определению, сравнивая префиксы и суффиксы строк.
Псевдокод
Prefix_function () = [0,..0] for i = 1 to n for k = 1 to i - 1 if s[1..k] == s[i - k + 1..i] [i] = k return
Пример
Рассмотрим строку abcabcd, для которой значение префикс-функции равно .
| Шаг | Строка | Значение функции |
|---|---|---|
| a | 0 | |
| ab | 0 | |
| abc | 0 | |
| abca | 1 | |
| abcab | 2 | |
| abcabc | 3 | |
| abcabcd | 0 |
Время работы
Всего итераций цикла, на каждой из который происходит сравнение строк за , что дает в итоге .
Оптимизация
Вносятся несколько важных замечаний:
- Следует заметить, что . Действительно, если , тогда . Значит в не максимально возможное значение, получено противоречие.
- Нужно избавиться от явных сравнений строк. Пусть вычислено и , тогда . Если отличается от , то нужно найти наибольшую длину , для которой верно . Когда найдется такое достаточно будет сравнить и , при их равенстве будет верно. Итеративно продолжается поиск , пока оно больше нуля. Если , то при значение , иначе нулю. Общая схема алгоритма есть, теперь нужно научиться искать .
- За исходное нужно взять , что следует из первого пункта. В случае, когда символы и не совпадают, — следующая по максимальности длина потенциального наибольшего общего префикса, что видно из рисунка. Последнее утверждение верно, пока , что позволит всегда найти его следующее значение.
Псевдокод
Prefix_function () [1] = 0 k = 0 for i = 2 to n while k > 0 && s[i] != s[k + 1] k = [k] if s[i] == s[k + 1] k++ [i] = k return
Время работы
Время работы алгоритма составит . Для доказательства этого потребуется новое обозначение — количество итераций цикла на -ом шаге. Итоговое время работы алгоритма составит . Теперь стоит отметить, что увеличивается на каждом шаге не более чем на единицу, значит максимально возможное значение Внутри цикла значение лишь уменьшается, а из предыдущего утверждения получается, что оно не может уменьшиться больше, чем раз, значит , что дает итоговую оценку времени алгоритма .
Литература
Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296.