Сведение задачи RMQ к задаче LCA

Постановка задачи RMQ

Пример построенного дерева для массива А

Дан массив [math]A[1..N][/math]. Поступают запросы вида [math](i, j)[/math], на каждый запрос требуется найти минимум в массиве [math]A[/math], начиная с позиции [math]i[/math] и заканчивая позицией [math]j[/math].

Алгоритм

Декартово дерево (англ. сartesian tree) по неявному ключу на массиве [math]A[1..N][/math] — это бинарное дерево, допускающее следующее рекурсивное построение:

• Корнем дерева является элемент массива, имеющий минимальное значение [math]A[/math], скажем [math]A[i][/math]. Если минимальных элементов несколько, можно взять любой.
• Левым поддеревом является декартово дерево на массиве [math]A[1..i-1][/math].
• Правым поддеревом является декартово дерево на массиве [math]A[i+1..N][/math].

Здесь и далее [math]A[i][/math] будет также использоваться для обозначения соответствующей вершины дерева.

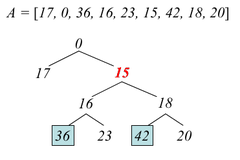
Построим декартово дерево на массиве [math]A[/math]. Тогда [math]RMQ(i, j)[/math] = [math]LCA(A[i], A[j])[/math].

Доказательство

Теорема:

[math]RMQ(i, j)[/math] = [math]LCA(A[i], A[j])[/math].

Доказательство:

[math]\triangleright[/math]

Положим [math]w = LCA(A[i], A[j])[/math]. Заметим, что [math]A[i][/math] и [math]A[j][/math] не принадлежат одновременно либо правому, либо левому поддереву [math]w[/math], потому как тогда бы соответствующий сын находился на большей глубине, чем [math]w[/math], и также являлся предком как [math]A[i][/math] так и [math]A[j][/math], что противоречит определению [math]LCA[/math]. Из этого замечанию следует, что [math]w[/math] лежит между [math]A[i][/math] и [math]A[j][/math] и, следовательно, принадлежит отрезку [math]A[i..j][/math]. По построению мы также знаем, что: Любая вершина дерева имеет свое значение меньшим либо равным значению её детей. Поддерево с корнем в [math]w[/math] содержит в себе подмассив [math]A[i..j][/math]. Суммируя, получаем, что [math]w[/math] имеет минимальное значение на отрезке, покрывающем [math]A[i..j][/math], и принадлежит отрезку [math]A[i..j][/math], отсюда [math]RMQ(i, j) = w[/math].

[math]\triangleleft[/math]

Сложность

Следующий алгоритм строит декартово дерево за [math]O(n)[/math]. Используя Сведение задачи LCA к задаче RMQ, получаем: препроцессинг для [math]LCA[/math] — [math]O(n)[/math] и ответ на запрос — [math]O(1)[/math]. В итоге получили [math]RMQ[/math] с построением за [math]O(n)[/math] и ответом на запрос за [math]O(1)[/math].

См.также

• Сведение задачи LCA к задаче RMQ
• Декартово дерево
• Алгоритм Фарака-Колтона и Бендера

Ссылки

• Задача RMQ. Решение за O (1) с препроцессингом O (N)