Очередь — различия между версиями
Whiplash (обсуждение | вклад) м (→pop) |
Genyaz (обсуждение | вклад) (Добавлена очередь на стеках в реальном времени) |
||
| Строка 96: | Строка 96: | ||
'''Минусы:''' | '''Минусы:''' | ||
* Если <tex>leftStack</tex> не пуст, то операция <tex>pop</tex> может выполняться <tex>O(n)</tex> времени, в отличии от других реализаций, где <tex>pop</tex> всегда выполняется за <tex>O(1)</tex> | * Если <tex>leftStack</tex> не пуст, то операция <tex>pop</tex> может выполняться <tex>O(n)</tex> времени, в отличии от других реализаций, где <tex>pop</tex> всегда выполняется за <tex>O(1)</tex> | ||
| + | |||
| + | == Реализация на пяти стеках == | ||
| + | Одним из минусов реализации на двух стеках является то, что в худшем случае мы тратим <tex>O(n)</tex> времени на операцию. Если распределить время, необходимое для перемещения элементов из одного стека в другой, по операциям, мы получим очередь без худших случаев с <tex>O(1)</tex> истинного времени на операцию. | ||
| + | |||
| + | Для такой очереди можно использовать либо шесть обычных стеков, либо два персистентных и три обычных. Рассмотрим последний вариант как более простой. | ||
| + | |||
| + | Пусть мы имеем стеки <tex>L, L', R, R', T</tex>, причем стеки <tex>L</tex> и <tex>L'</tex> используются для операций <tex>push</tex>, персистентные стеки <tex>R</tex> и <tex>R'</tex> используются для операций <tex>pop</tex>, а стек <tex>T</tex> используется для перекопирования элементов. | ||
| + | |||
| + | В каждый момент времени в очереди зафиксировано какой <tex>Lcur</tex> из стеков <tex>L</tex> и <tex>L'</tex> используется для помещения туда элементов, пришедших с операцией <tex>push</tex>, а также какой <tex>Rcur</tex> из стеков <tex>R</tex> и <tex>R'</tex> используется для извлечения оттуда элементов, запрашиваемых операцией <tex>pop</tex>. | ||
| + | |||
| + | Очередь будет работать в двух режимах: | ||
| + | # Обычный режим, аналогично реализации на двух стеках. | ||
| + | # Режим перекопирования (''recopy mode''). Этот режим активируется, когда при очередной операции в обычном режиме в стеке <tex>Lcur</tex> становится больше элементов, чем в стеке <tex>Rcur</tex>. | ||
| + | |||
| + | При активации режима перекопирования: | ||
| + | * Инициализируется счетчик <tex>toCopy=Rcur.size+Lcur.size</tex>, который означает, сколько элементов нужно будет скопировать из <tex>T</tex>. | ||
| + | * Текущий стек для операций <tex>push</tex> меняется с <tex>Lcur</tex> на другой стек. | ||
| + | |||
| + | В режиме перекопирования на каждую операцию выполняются дополнительные действия. Поскольку в этом режиме остаются корректными все операции <tex>push</tex> и <tex>Rcur.size</tex> операций <tex>pop</tex>, которые мы сможем выполнить на персистентном стеке <tex>Rcur</tex>, можно предполагать, что на перекопирование у нас есть по крайней мере <tex>n + 1 = Rcur.size + 1</tex> операций, включая ту, которая активировала этот режим. | ||
| + | |||
| + | Суммарно за эти операции мы должны сделать: | ||
| + | # Перемещение содержимого стека <tex>Rcur</tex> в стек <tex>T</tex>, это <tex>n</tex> операций. | ||
| + | # Перемещение содержимого стека <tex>Lcur</tex> в стек <tex>T</tex>, это <tex>n + 1</tex> операция. | ||
| + | # Перемещение содержимого стека <tex>T</tex> во второй стек для извлечения, это <tex>2 \cdot n + 1</tex> операций. | ||
| + | |||
| + | Счетчик <tex>toCopy</tex> уменьшается в двух случаях: | ||
| + | * Мы переместили часть содержимого <tex>T</tex> в стек для извлечения. | ||
| + | * Нам пришел запрос <tex>pop</tex> и мы уменьшили <tex>toCopy</tex> на 1, чтобы показать, что один из элементов <tex>Rcur</tex> на дне <tex>T</tex> уже был извлечен. | ||
| + | |||
| + | Итого имеем суммарно <tex>4 \cdot n + 2</tex> дополнительные стековые операции, которые мы должны сделать за <tex>n + 1</tex> операций, то есть <tex>4</tex> дополнительных операции на одну обычную, что означает <tex>O(1)</tex> истинного времени на операцию. | ||
| + | |||
| + | |||
== См. также == | == См. также == | ||
Версия 17:42, 5 июня 2013
Содержание
Определение
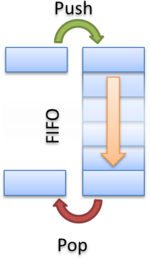
Очередь (Queue) — это структура данных, добавление и удаление элементов в которой происходит путём операций Push и Pop соответственно. Притом первым из очереди удаляется элемент, который был помещен туда первым, то есть в очереди реализуется принцип «первым вошел — первым вышел» (first-in, first-out — FIFO). У очереди имеется голова (head) и хвост (tail). Когда элемент ставится в очередь, он занимает место в её хвосте. Из очереди всегда выводится элемент, который находится в ее голове.
- (запись в очередь) - операция вставки нового элемента.
- (снятие с очереди) - операция удаления нового элемента.
- - проверка очереди на наличие в ней элементов
Реализация на массиве
Очередь, способную вместить не более элементов, можно реализовать с помощью массива . Она будет обладать следующими полями:
- (голова очереди)
- (хвост очереди)
- (размер очереди)
push
push(x) elements[tail] = x tail = (tail + 1) % elements.length size++
pop
pop()
if !empty()
x = elements[head]
head = (head + 1) % elements.length
size--
return x
empty
empty() return size == 0
Из-за того что нам не нужно перевыделять память, каждая операция выполняется за времени.
Плюсы:
- - прост в разработке
- - по сравнению с реализацией на списке, есть незначительная экономия памяти
Минусы:
- - количество элементов в очереди ограничено размером массива (исправляется написанием функции расширения массива)
- - при переполнении очереди требуется перевыделение памяти и копирование всех элементов в новый массив
Реализация на списке
Для данной реализации очереди необходимо создать список () и операции работы на созданном списке.
Реализация очереди на односвязном списке:
list
- - поле, в котором хранится значение элемента
- - указатель на следующий элемент очереди
push
push(x)
element = tail
tail = new list(x, NULL)
if size == 0
head = tail
else
element.next = tail
size++
pop
pop()
if empty()
return
element = head
head = head.next
size--
return element
empty
empty() return size == 0
Каждая операция выполняется за время .
Минусы:
- Память фрагментируется гораздо сильнее и последовательная итерация по такой очереди может быть ощутимо медленнее, нежели итерация по очереди реализованной на массиве
Реализация на двух стеках
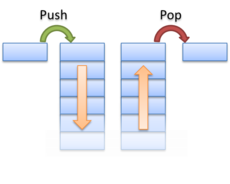
Очередь можно реализовать на двух стеках и . Один из стеков будем использовать для операции , другой для операции . При этом, если при попытке извлечения элемента из он оказался пустым, просто перенесем все элементы из в него (при этом элементы в получатся уже в обратном порядке, что нам и нужно для извлечения элементов, а станет пустым).
- и - функции, реализующие операцию для соответствующего стека;
- и - аналогично операции .
push
push(x) pushLeft(x)
pop
if !rigthStack.empty()
return popRight()
else
while !leftStack.empty()
pushRight(popLeft())
return popRight()
При выполнении операции будем использовать три монеты: одну для самой операции, вторую в качестве резерва на операцию из первого стека, третью во второй стек на финальный . Тогда для операций учётную стоимость можно принять равной нулю и использовать для операции монеты, оставшиеся после операции .
Таким образом, для каждой операции требуется монет, а значит, амортизационная стоимость операций .
Минусы:
- Если не пуст, то операция может выполняться времени, в отличии от других реализаций, где всегда выполняется за
Реализация на пяти стеках
Одним из минусов реализации на двух стеках является то, что в худшем случае мы тратим времени на операцию. Если распределить время, необходимое для перемещения элементов из одного стека в другой, по операциям, мы получим очередь без худших случаев с истинного времени на операцию.
Для такой очереди можно использовать либо шесть обычных стеков, либо два персистентных и три обычных. Рассмотрим последний вариант как более простой.
Пусть мы имеем стеки , причем стеки и используются для операций , персистентные стеки и используются для операций , а стек используется для перекопирования элементов.
В каждый момент времени в очереди зафиксировано какой из стеков и используется для помещения туда элементов, пришедших с операцией , а также какой из стеков и используется для извлечения оттуда элементов, запрашиваемых операцией .
Очередь будет работать в двух режимах:
- Обычный режим, аналогично реализации на двух стеках.
- Режим перекопирования (recopy mode). Этот режим активируется, когда при очередной операции в обычном режиме в стеке становится больше элементов, чем в стеке .
При активации режима перекопирования:
- Инициализируется счетчик , который означает, сколько элементов нужно будет скопировать из .
- Текущий стек для операций меняется с на другой стек.
В режиме перекопирования на каждую операцию выполняются дополнительные действия. Поскольку в этом режиме остаются корректными все операции и операций , которые мы сможем выполнить на персистентном стеке , можно предполагать, что на перекопирование у нас есть по крайней мере операций, включая ту, которая активировала этот режим.
Суммарно за эти операции мы должны сделать:
- Перемещение содержимого стека в стек , это операций.
- Перемещение содержимого стека в стек , это операция.
- Перемещение содержимого стека во второй стек для извлечения, это операций.
Счетчик уменьшается в двух случаях:
- Мы переместили часть содержимого в стек для извлечения.
- Нам пришел запрос и мы уменьшили на 1, чтобы показать, что один из элементов на дне уже был извлечен.
Итого имеем суммарно дополнительные стековые операции, которые мы должны сделать за операций, то есть дополнительных операции на одну обычную, что означает истинного времени на операцию.
См. также
Ссылки
- Википедия - Очередь (программирование)
- Т. Кормен. «Алгоритмы. Построение и анализ» второе издание, Глава 10.1, стр. 262
- T. H. Cormen. «Introduction to Algorithms» third edition, Chapter 10.1, p. 262