Meet-in-the-middle — различия между версиями
Dronov (обсуждение | вклад) |
Dronov (обсуждение | вклад) |
||
| Строка 41: | Строка 41: | ||
Таким образом, bfs-ом из двух концов, мы сгенерируем максимум <tex> {O({K^{n/2}})} </tex> состояний. | Таким образом, bfs-ом из двух концов, мы сгенерируем максимум <tex> {O({K^{n/2}})} </tex> состояний. | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | |||
| + | [[Категория: Динамическое программирование ]] | ||
Версия 00:37, 16 декабря 2012
| Определение: |
| Meet-in-the-middle (Встреча в середине) — способ оптимизации перебора. |
Алгоритм Meet-in-the-middle разбивает задачу пополам и решает всю задачу через частичный расчет
Содержание
Задача о рюкзаке
Классической задачей является задача о наиболее эффективной упаковке рюкзака. Каждый предмет характеризуется весом ( ) и ценностью (). В рюкзак, ограниченный по весу, необходимо набрать вещей с максимальной суммарной стоимостью. Для ее решения изначальное множество вещей N разбивается на два равных(или примерно равных) подмножества, для которых за приемлемое время, можно перебрать все варианты и подсчитать суммарный вес и стоимость, а затем для каждого из них найти группу вещей из первого подмножества с максимальной стоимостью, укладывающуюся в ограничение по весу рюкзака. Сложность алгоритма . Память
Реализация
Реализуем данный алгоритм:
// N - количество всех вещей, w[] - массив весов всех вещей, cost[] - массив стоимостей всех вещей, R - ограничение по весу рюкзака.
sn = N / 2, fn = N - sn;
for mask = 0 to 2 ** sn - 1
for j = 0 to sn
if j-ый бит mask = 1
first[i].w += w[j];
first[i].c += cost[j];
for mask = 0 to 2 ** fn - 1
for j = 0 to fn
if j-ый бит mask = 1
curw += w[j];
curcost += cost[j];
p = findmax(); // Находим маску вещей из первой половины с макcимальной стоимостью и подходящей по весу
if (curw + first[p].w < R && curcost + first[p].c > ans)
ans = curcost + first[p].c
print ans
Задача о нахождение кратчайшего расстояния между двумя вершинами в графе
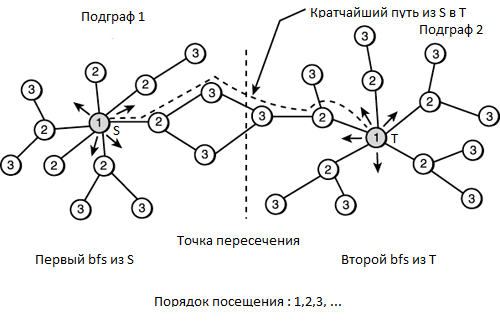
Еще одна задача, решаемая алгоритмом Meet-in-the-middle — это нахождение кратчайшего расстояния между двумя вершинами, зная начальное состояние, конечное состояние и то, что длина оптимального пути не превышает N.
Стандартным подходом для решения данной задачи, является применение алгоритма обхода в ширину. Пусть из каждого состояние у нас есть K переходов, тогда бы мы сгенерировали состояний. Асимптотика данного рещения составила бы . Meet-in-the-middle помогает снизить асимптотику до .
Алгоритм решения
1. Сгенерируем bfs-ом все состояния, доступные из начала и конца за или меньше ходов.
2. Найдем состояний, которые достижимы из начала и из конца.
3. Найдем среди них наилучшее по сумме длин путей.
Таким образом, bfs-ом из двух концов, мы сгенерируем максимум состояний.