Динамика по поддеревьям — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Динамика по дереву)
Строка 1: Строка 1:
−
=Динамика по дереву=
+
=Динамика по деревьям=
  
 
Рассмотрим динамику по дереву на примере задачи о максимальном независимом множестве в дереве.
 
Рассмотрим динамику по дереву на примере задачи о максимальном независимом множестве в дереве.
−
{{Определение
+
==Задача о максимальном независимом множестве на дереве==
−
|neat = 1 - параметр нужен для того, чтобы определение не растягивалось на всю страницу(не обязательно)
+
===Формулировка===
−
|definition=Пусть дано подвешенное за корень дерево, имеющее веса на каждой из ее вершин. Необходимо выбрать такое множество вершин, что бы сумма значений была максимальной и при этом выбранные вершины не являлись бы друг-другу соседями (отец-сын).  
+
Пусть дано подвешенное за корень дерево, имеющее веса на каждой из ее вершин. Необходимо выбрать такое множество вершин, что бы сумма значений была максимальной и при этом выбранные вершины не являлись бы друг-другу соседями (отец-сын).  
−
}}
+
===Решение===
 
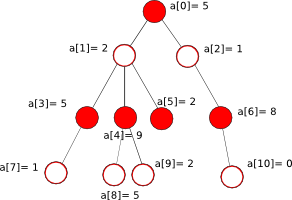
[[Файл:Independent_set_tree.png|100px|right|frame|Независимый набор из красных вершин]]
 
[[Файл:Independent_set_tree.png|100px|right|frame|Независимый набор из красных вершин]]
 +
Давайте заметим, что в случае дерева эта задача имеет решение методом динамического программирования, в отличии от общего случая на произвольном множестве. Это обобщение относится к классу NP-полных задач.
 +
Главное отличие этой задачи от других динамически решаемых {{---}} ответ в одном поддереве влияет на решение в остальных.
 +
 +
Рассмотрим наше первое состояние, когда еще не выбрана ни одна вершина. В этом случае мы можем сделать две вещи:
 +
* Взять корень в наше множество
 +
* Не взять корень в наше множество
 +
 +
В первом случае мы не сможем рассматривать его детей вовсе (т.е. при переходе в его поддеревья, мы не будем рассматривать возможность добавления корня в множество). В ином случае мы переходим в его поддеревья и выполняем то же самое действие.
 +
 +
===Рекуррентная формула===
 +
Заметим, что в случае взятия корня мы сразу же можем перейти к внукам нашего корня.
 +
 +
<tex>I(u) = \max\left\{a[u]\ +\  \sum_{\text{grandchild}\ w\  of\  u}I(w),\ \sum_{\text{child}\  w\  of\  u}I(w) \right\},</tex>
 +
 +
===Псевдокод===
 +
    function calculate(v):
 +
        if dp[v] != -1:
 +
            return dp[v]
 +
            #вернули уже посчитанное значение dp[v]
 +
        sum1 = 0
 +
        #случай 1: не берем корень
 +
        for u in child(v):
 +
            sum1 += calculate(u)
 +
        sum2 = a[v]
 +
        #случай 2: берем корень
 +
        for u in child(v):
 +
            for t in child(u): # считаем, что у нас нет ребер наверх, к корню
 +
                sum2 += calculate(t)
 +
        # выполняем мемоизацию
 +
        dp[v] = max(sum1, sum2)
 +
        return dp[v]
 +
 +
child(v) -- возвращает детей вершины v
 +
 +
==Общие принципы динамики по поддеревьям==
 +
Самое главное и основное отличие {{---}} ответ в одном поддереве может влиять на другие ответы, как в предыдущей задаче влиял выбор корня.

Версия 19:00, 13 января 2013

Динамика по деревьям

Рассмотрим динамику по дереву на примере задачи о максимальном независимом множестве в дереве.

Задача о максимальном независимом множестве на дереве

Формулировка

Пусть дано подвешенное за корень дерево, имеющее веса на каждой из ее вершин. Необходимо выбрать такое множество вершин, что бы сумма значений была максимальной и при этом выбранные вершины не являлись бы друг-другу соседями (отец-сын).

Решение

Независимый набор из красных вершин

Давайте заметим, что в случае дерева эта задача имеет решение методом динамического программирования, в отличии от общего случая на произвольном множестве. Это обобщение относится к классу NP-полных задач. Главное отличие этой задачи от других динамически решаемых — ответ в одном поддереве влияет на решение в остальных.

Рассмотрим наше первое состояние, когда еще не выбрана ни одна вершина. В этом случае мы можем сделать две вещи:

  • Взять корень в наше множество
  • Не взять корень в наше множество

В первом случае мы не сможем рассматривать его детей вовсе (т.е. при переходе в его поддеревья, мы не будем рассматривать возможность добавления корня в множество). В ином случае мы переходим в его поддеревья и выполняем то же самое действие.

Рекуррентная формула

Заметим, что в случае взятия корня мы сразу же можем перейти к внукам нашего корня.

[math]I(u) = \max\left\{a[u]\ +\ \sum_{\text{grandchild}\ w\ of\ u}I(w),\ \sum_{\text{child}\ w\ of\ u}I(w) \right\},[/math]

Псевдокод

   function calculate(v):
       if dp[v] != -1:
           return dp[v]
           #вернули уже посчитанное значение dp[v]
       sum1 = 0
       #случай 1: не берем корень
       for u in child(v):
           sum1 += calculate(u)
       sum2 = a[v]
       #случай 2: берем корень
       for u in child(v):
           for t in child(u): # считаем, что у нас нет ребер наверх, к корню
               sum2 += calculate(t)
       # выполняем мемоизацию
       dp[v] = max(sum1, sum2)
       return dp[v]

child(v) -- возвращает детей вершины v

Общие принципы динамики по поддеревьям

Самое главное и основное отличие — ответ в одном поддереве может влиять на другие ответы, как в предыдущей задаче влиял выбор корня.

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Динамика_по_поддеревьям&oldid=29568»