Детерминированные конечные автоматы — различия между версиями
(→Детерминированный конечный автомат) |
|||
| Строка 5: | Строка 5: | ||
Детерминированный конечный автомат(ДКА) --- набор из пяти элементов <tex>\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to Q \rangle</tex>, где <tex>\Sigma</tex> -- алфавит, <tex>Q</tex> -- множество состояний автомата, <tex>s</tex> -- начальное состояние автомата, <tex>T</tex> -- Множество допускающих состояний автомата, <tex>\delta</tex> -- функция переходов. | Детерминированный конечный автомат(ДКА) --- набор из пяти элементов <tex>\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to Q \rangle</tex>, где <tex>\Sigma</tex> -- алфавит, <tex>Q</tex> -- множество состояний автомата, <tex>s</tex> -- начальное состояние автомата, <tex>T</tex> -- Множество допускающих состояний автомата, <tex>\delta</tex> -- функция переходов. | ||
}} | }} | ||
| + | |||
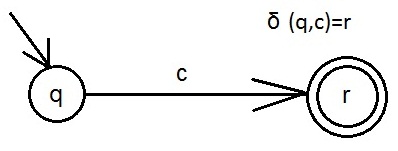
| + | Пример : | ||
| + | |||
| + | [[Файл:DKA_1.jpg]] | ||
| + | |||
=== Процесс допуска === | === Процесс допуска === | ||
Процесс допуска слова автоматом выглядит так: | Процесс допуска слова автоматом выглядит так: | ||
* Изначально автомат находится в стартовом состоянии | * Изначально автомат находится в стартовом состоянии | ||
* Ему на вход подается строка | * Ему на вход подается строка | ||
| − | * Далее на каждом шагу автомат берет новый символ строки и совершает соответствующий переход в новое состояние, ''если для символа не задано никакого перехода из текущего состояния, то слово считается недопущенным | + | * Далее на каждом шагу автомат берет новый символ строки и совершает соответствующий переход в новое состояние, ''если для символа не задано никакого перехода из текущего состояния, то слово считается недопущенным '' |
* Слово считается допущенным, если после того, как прочитаны все его символы, автомат оказался в допускающем состоянии. | * Слово считается допущенным, если после того, как прочитаны все его символы, автомат оказался в допускающем состоянии. | ||
| + | |||
| + | == Обозначения == | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Мгновенное описание (конфигурация) - <q , α>, где q – текущее состояние, α – оставшиеся символы. | ||
| + | }} | ||
Для удобства можно ввести следующие обозначения: | Для удобства можно ввести следующие обозначения: | ||
| + | |||
| + | 1.Переход за 1 шаг: | ||
* <tex>\langle q, \alpha \rangle \vdash \langle p, \beta \rangle</tex>, если | * <tex>\langle q, \alpha \rangle \vdash \langle p, \beta \rangle</tex>, если | ||
** <tex>\alpha = c\beta</tex> | ** <tex>\alpha = c\beta</tex> | ||
** <tex>\delta (q, c)=p </tex> | ** <tex>\delta (q, c)=p </tex> | ||
| − | + | 2.Переход за 0 или более шагов: | |
* <tex>\langle q, \alpha \rangle \vdash^* \langle p, \beta \rangle</tex>, если | * <tex>\langle q, \alpha \rangle \vdash^* \langle p, \beta \rangle</tex>, если | ||
** <tex>\langle q, c_1 c_2 c_3 ...c_n\beta \rangle \vdash \langle u_1, c_2 c_3 ...c_n\beta \rangle \vdash \langle u_2, c_3 ...c_n\beta \rangle ...\vdash \langle u_{n-1}, c_n\beta \rangle \vdash \langle p, \beta \rangle</tex> | ** <tex>\langle q, c_1 c_2 c_3 ...c_n\beta \rangle \vdash \langle u_1, c_2 c_3 ...c_n\beta \rangle \vdash \langle u_2, c_3 ...c_n\beta \rangle ...\vdash \langle u_{n-1}, c_n\beta \rangle \vdash \langle p, \beta \rangle</tex> | ||
| + | |||
| + | === Автоматные языки === | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | <tex>L(\mathcal{A})=\{\alpha| \langle s, \alpha \rangle \vdash^* \langle t, \varepsilon \rangle t \in T\}</tex> --- язык автомата <tex>\mathcal{A}</tex>. | ||
| + | }} | ||
| + | |||
| + | Пример: | ||
| + | |||
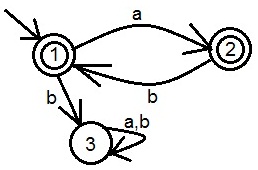
| + | Автомат, допускающий слова над алфавитом из символов a и b, допускающий слова в которых перед каждым символом b идёт символ a. | ||
| + | |||
| + | (a|ab)* | ||
| + | |||
| + | [[Файл:DKA_2.jpg]] | ||
| + | |||
{{Лемма | {{Лемма | ||
| Строка 27: | Строка 56: | ||
}} | }} | ||
| − | == | + | |
| − | + | == Способ хранения автомата == | |
| − | + | ||
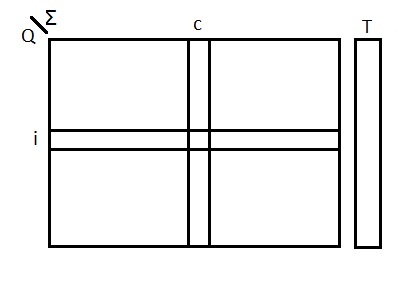
| − | + | [[Файл:save_DKA.jpg]] | |
| − | + | ||
| + | В ячейке таблицы (i, c) храним номер состояния, в которое можно перейти из состояния i по символу c. В массиве Access отмечены допускающие состояния. Таким образом требуется O(|Q||Σ|) памяти. | ||
Версия 05:03, 5 октября 2010
Содержание
Детерминированный конечный автомат
| Определение: |
| Детерминированный конечный автомат(ДКА) --- набор из пяти элементов , где -- алфавит, -- множество состояний автомата, -- начальное состояние автомата, -- Множество допускающих состояний автомата, -- функция переходов. |
Пример :
Процесс допуска
Процесс допуска слова автоматом выглядит так:
- Изначально автомат находится в стартовом состоянии
- Ему на вход подается строка
- Далее на каждом шагу автомат берет новый символ строки и совершает соответствующий переход в новое состояние, если для символа не задано никакого перехода из текущего состояния, то слово считается недопущенным
- Слово считается допущенным, если после того, как прочитаны все его символы, автомат оказался в допускающем состоянии.
Обозначения
| Определение: | ||||||||
Мгновенное описание (конфигурация) - , где q – текущее состояние, α – оставшиеся символы.</td></tr> |