Недетерминированные конечные автоматы — различия между версиями
(→Пример) |
(→Способ хранения) |
||
| Строка 22: | Строка 22: | ||
== Способ хранения == | == Способ хранения == | ||
| − | + | Срособ хранения НКА отличается от ДКА лишь тем, что в ячейке таблицы хранится список состояний, в которые возможен переход по данному символу. | |
Память <tex>|Q|^2||\Sigma|</tex>. | Память <tex>|Q|^2||\Sigma|</tex>. | ||
| − | |||
== Теорема == | == Теорема == | ||
Версия 23:36, 5 октября 2010
Содержание
Недетерминированный конечный автомат
| Определение: |
| Недетерминированный конечный автомат(НКА) --- набор из пяти элементов , где -- алфавит, -- множество состояний автомата, -- начальное состояние автомата, -- Множество допускающих состояний автомата, -- функция переходов. Таким образом НКА - это ДКА с возможностью нескольких переходов по одному символу из одного состояния. |
Язак автомата
| Определение: |
| --- язык автомата . |
Пример
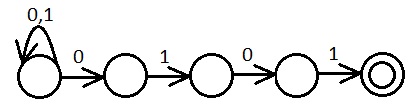
Автомат, допускающий слова над алфавитом из символов 0 и 1, допускающий слова оканчивающиеся на 0101.
(0|1)*0101
Способ хранения
Срособ хранения НКА отличается от ДКА лишь тем, что в ячейке таблицы хранится список состояний, в которые возможен переход по данному символу.
Память .
Теорема
| Теорема: |
α(ДКА) = α(НКА) |
| Доказательство: |
| proof. |