Антисимметричное отношение — различия между версиями
Savelin (обсуждение | вклад) (англоязычные термины, ссылка на асимметричность (википедия), внешние ссылки исправлены на внутренние) |
|||
| Строка 32: | Строка 32: | ||
Антисимметрично отношение делимости на натуральных числах (если <tex>a \mid b</tex> и <tex>b \mid a</tex>, то <tex>a=b</tex>) | Антисимметрично отношение делимости на натуральных числах (если <tex>a \mid b</tex> и <tex>b \mid a</tex>, то <tex>a=b</tex>) | ||
| − | Отношение включения на <tex>2^U</tex>, где <tex>U</tex> - универсум, антисимметрично (<tex> A \subseteq B \wedge B \subseteq A \Rightarrow A = B</tex>). | + | Отношение включения на <tex>2^U</tex>, где <tex>U</tex> {{---}} универсум, антисимметрично (<tex> A \subseteq B \wedge B \subseteq A \Rightarrow A = B</tex>). |
== Свойства антисимметричного отношения == | == Свойства антисимметричного отношения == | ||
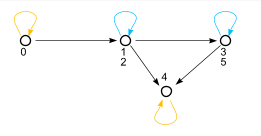
| − | [[Файл:antisym.png| | + | [[Файл:antisym.png|400px|thumb|right|Граф антисимметричного отношения (не имеет кратных ребер)]] |
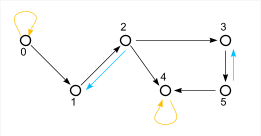
| − | [[Файл:nonantisym.png| | + | [[Файл:nonantisym.png|400px|thumb|right|Граф отношения, не являющегося антисимметричным]] |
Матрица смежности антисимметричного отношения может содержать единицы на главной диагонали, притом если элемент <tex>a_{ij}</tex> матрицы равен единице, то элемент <tex>a_{ji}</tex> равен нулю. | Матрица смежности антисимметричного отношения может содержать единицы на главной диагонали, притом если элемент <tex>a_{ij}</tex> матрицы равен единице, то элемент <tex>a_{ji}</tex> равен нулю. | ||
| Строка 60: | Строка 60: | ||
Ориентированный граф, изображающий антисимметричное отношение, не имеет двух дуг с противоположной ориентацией между двумя различными вершинами, однако в нём могут быть петли. | Ориентированный граф, изображающий антисимметричное отношение, не имеет двух дуг с противоположной ориентацией между двумя различными вершинами, однако в нём могут быть петли. | ||
| − | Если <tex>a</tex> и <tex>b</tex> - некоторые антисимметричные отношения, то антисимметричными также являются отношения: | + | Если <tex>a</tex> и <tex>b</tex> {{---}} некоторые антисимметричные отношения, то антисимметричными также являются отношения: |
#<tex>a\cap b</tex> | #<tex>a\cap b</tex> | ||
#<tex>a^{-1}</tex> | #<tex>a^{-1}</tex> | ||
| Строка 70: | Строка 70: | ||
* [[Симметричное отношение]] | * [[Симметричное отношение]] | ||
| − | == Источники == | + | == Источники информации == |
* [http://ru.wikipedia.org/wiki/Антисимметричное_отношение Антисимметричное отношение {{---}} Википедия] | * [http://ru.wikipedia.org/wiki/Антисимметричное_отношение Антисимметричное отношение {{---}} Википедия] | ||
* [http://en.wikipedia.org/wiki/Antisymmetric_relation Антисимметричное отношение {{---}} статья на английской Википедии] | * [http://en.wikipedia.org/wiki/Antisymmetric_relation Антисимметричное отношение {{---}} статья на английской Википедии] | ||
* [http://www.madi.ru/study/kafedra/asu_new/metod_new/mil/tpr09_13.shtml#1 Статья на сайте МАДИ] | * [http://www.madi.ru/study/kafedra/asu_new/metod_new/mil/tpr09_13.shtml#1 Статья на сайте МАДИ] | ||
| − | |||
| − | |||
* [http://en.wikipedia.org/wiki/Asymmetric_relation Wikipedia | Asymmetric relation] | * [http://en.wikipedia.org/wiki/Asymmetric_relation Wikipedia | Asymmetric relation] | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Отношения]] | [[Категория: Отношения]] | ||
Версия 01:00, 16 октября 2014
Содержание
Основные определения
| Определение: |
| Бинарное отношение на множестве называется антисимметричным (англ. antisymmetric binary relation), если для любых элементов и множества из выполнения отношений и следует равенство и . |
Или эквивалентное
| Определение: |
| Бинарное отношение на множестве называется антисимметричным, если для любых неравных элементов и множества из выполнения отношения следует невыполнение отношения . |
Определение антисимметричного отношения как является избыточным (и потому неверным), поскольку из такого определения также следует антирефлексивность R.
Антисимметричность отношения не исключает симметричности. Существуют бинарные отношения:
- одновременно симметричные и антисимметричные (отношение равенства);
- ни симметричные, ни антисимметричные;
- симметричные, но не антисимметричные;
- антисимметричные, но не симметричные ("меньше или равно", "больше или равно");
Антирефлексивное антисимметричное отношение иногда называют асимметричным. Следует различать эти два понятия. Формальное определение:
| Определение: |
| Бинарное отношение на множестве называется асимметричным (англ. asymmetric binary relation), если для любых элементов и множества одновременное выполнение отношений и невозможно. |
Примеры антисимметричных отношений
Примерами антисимметричных отношений являются, по определению, все отношения полного и частичного порядка ( и другие).
Антисимметрично отношение делимости на натуральных числах (если и , то )
Отношение включения на , где — универсум, антисимметрично ().
Свойства антисимметричного отношения
Матрица смежности антисимметричного отношения может содержать единицы на главной диагонали, притом если элемент матрицы равен единице, то элемент равен нулю.
Например, если — матрица смежности отношения "" на ; — матрица смежности отношения делимости на том же множестве , то
Ориентированный граф, изображающий антисимметричное отношение, не имеет двух дуг с противоположной ориентацией между двумя различными вершинами, однако в нём могут быть петли.
Если и — некоторые антисимметричные отношения, то антисимметричными также являются отношения:
Однако объединение и композиция и могут не сохранять антисимметричности.