Теорема Гринберга — различия между версиями
Slavian (обсуждение | вклад) |
Slavian (обсуждение | вклад) |
||
| Строка 28: | Строка 28: | ||
Левая часть соотношения <math>\sum_{i=3}^{V(G)}(i-2)(k_i-k'_i)=0</math> в таком графе, очевидно, не делится на <tex>3</tex>, так как сравнима по модулю <tex>3</tex> с <tex>(9 - 2)(k_9 − k'_9) = 7</tex>. | Левая часть соотношения <math>\sum_{i=3}^{V(G)}(i-2)(k_i-k'_i)=0</math> в таком графе, очевидно, не делится на <tex>3</tex>, так как сравнима по модулю <tex>3</tex> с <tex>(9 - 2)(k_9 − k'_9) = 7</tex>. | ||
[[Файл: Grinberg_Graph.png|300px|thumb|right|Граф Гринберга]] | [[Файл: Grinberg_Graph.png|300px|thumb|right|Граф Гринберга]] | ||
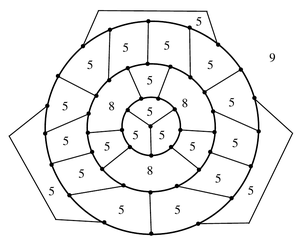
| − | [[Файл: Grinberg_Graph_numbers.png|300px|thumb|left|Граф Гринберга | + | [[Файл: Grinberg_Graph_numbers.png|300px|thumb|left|Граф Гринберга. Проставлено количество ребер в гранях.]] |
| + | |||
| + | |||
| + | == Источники == | ||
| + | *[http://en.wikipedia.org/wiki/Grinberg%27s_theorem Теорема Гринберга - википедия] | ||
| + | *[http://logic.pdmi.ras.ru/~dvk/211/graphs_dk.pdf Д.В Карпов - теория графов] | ||
| + | *[http://www.math.yorku.ca/Who/Faculty/Steprans/Courses/1200/Tutorial4.pdf теорема Гринберга] | ||
| + | |||
| + | [[Категория:Алгоритмы и структуры данных]] | ||
| + | [[Категория:Обходы графов]] | ||
Версия 01:20, 24 декабря 2013
Теорема Гринберга(англ. Grinberg) - необходимое условие содержания гамильтонова цикла планарным графом.
| Теорема (Гринберга): |
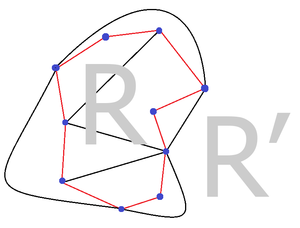
Пусть плоский граф без петель с гамильтоновым циклом , который делит плоскости на две области и . Пусть и — количества граней размера в и соответственно. Тогда
|
| Доказательство: |
|
Отметим, что в гамильтоновом графе , очевидно, нет мостов и граница любой грани — простой цикл. Поэтому размер границы каждой его грани не более . Пусть и — количества рёбер графа , лежащих внутри областей и соответственно. Так как — гамильтонов цикл графа , то область R разбита на граней. а область — на граней. Получаем соотношения: (1) , Каждое внутреннее ребро области входит в границы двух внутренних граней области , а каждое ребро цикла — в границу одной внутренней грани этой области. Аналогичное соотношение верно и для . Следовательно, (2) , Из соотношений (1) и (2) получаем: откуда немедленно следует доказываемое утверждение. |
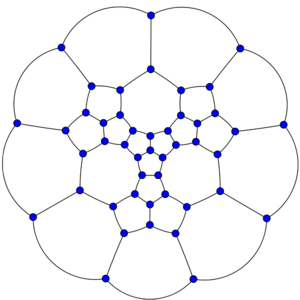
Используя свою теорему, Гринберг построил трёхсвязный кубический плоский граф, в котором ровно одна грань имеет рёбер, а все остальные — по или рёбер.
Левая часть соотношения в таком графе, очевидно, не делится на , так как сравнима по модулю с .