Диаметр множества точек (вращающиеся калиперы)

Эта статья находится в разработке!

Есть множество точек на плоскости. Нужно найти две самые удалённые из них.

Найдём выпуклую оболочку исходного множества и получим более простую задачу: найти две наиболее удалённые вершины в выпуклом многоугольнике. Сделать это можно за линейное время с помощью метода, который называется вращающиеся калиперы (англ. rotating calipers).

Постановка задачи

Пусть [math]P = (p_1, p_2, ... ,p_n)[/math] — выпуклый многоугольник, в котором порядок обхода вершин направлен против часовой стрелки, и никакие три последовательные точки не лежат на одной прямой. Найти пару чисел [math]\langle i, j \rangle[/math], такие, что [math]d(p_i, p_j)[/math] максимально.

Вращающиеся калиперы

Опорные прямые

Определение:

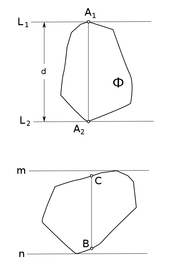
Прямая [math]L[/math] называется опорной прямой (англ. line of support) для многоугольника [math]P[/math], если его внутренность лежит по одну сторону от [math]L[/math], при этом [math]L[/math] проходит хотя бы через одну из вершин [math]P[/math].

Теорема: Пусть [math]L_1[/math] и [math]L_2[/math] — две параллельные опорные прямые фигуры [math]\Phi[/math], расстояние между которыми имеет максимальное значение. [math]A_1[/math] и [math]A_2[/math] — граничные точки фигуры [math]\Phi[/math], принадлежащие соответственно прямым [math]L_1[/math] и [math]L_2[/math]. Тогда отрезок [math]A_1A_2[/math] перпендикулярен обеим прямым [math]L_1[/math] и [math]L_2[/math]. Доказательство: [math]\triangleright[/math] Предположим, что это не так. Тогда расстояние между прямыми [math]L_1[/math] и [math]L_2[/math] было бы меньше, чем отрезок [math]A_1A_2[/math], и тем более меньше, чем расстояние между двумя опорными прямыми [math]L'_1[/math] и [math]L'_2[/math] фигуры [math]\Phi[/math], перпендикулярными к отрезку [math]A_1A_2[/math], что противоречит условию. [math]\triangleleft[/math]

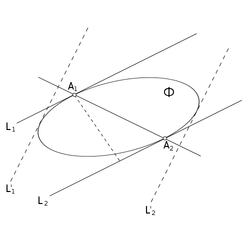
Так как [math]A_1[/math] и [math]A_2[/math] — какие угодно граничные точки фигуры [math]\Phi[/math], принадлежащие соответственно прямым [math]L_1[/math] и [math]L_2[/math], то из перпендикулярности отрезка [math]A_1A_2[/math] к прямым [math]L_1[/math] и [math]L_2[/math] следует, что ни одна из прямых [math]L_1[/math], [math]L_2[/math] не может иметь с фигурой [math]\Phi[/math] целый общий отрезок. Другими словами, каждая из этих прямых содержит единственную граничную точку фигуры [math]\Phi[/math].

Теорема: Диаметр выпуклого многоугольника равен максимальному расстоянию между параллельными опорными прямыми. Доказательство: [math]\triangleright[/math] Пусть [math]\Phi[/math] — выпуклая фигура, [math]L_1[/math] и [math]L_2[/math] — параллельные опорные прямые, расстояние между которыми имеет наибольшее возможное значение [math]d[/math], [math]A_1[/math] и [math]A_2[/math] — общие точки фигуры [math]\Phi[/math] и прямых [math]L_1[/math] и [math]L_2[/math] соответственно. По предыдущей теореме [math]A_1A_2[/math] перпендикулярен к прямым [math]L_1[/math], [math]L_2[/math], следовательно, его длина равна [math]d[/math]. Докажем, что расстояние между любыми двумя точками фигуры [math]\Phi[/math] не преводходит [math]d[/math]. Действительно, если [math]B[/math] и [math]C[/math] — какие-либо две точки фигуры [math]\Phi[/math], а [math]m[/math] и [math]n[/math] — опорные прямые, перпендикулярные к отрезку [math]BC[/math], то отрезок [math]BC[/math] не превосходит расстояния между прямыми [math]m[/math] и [math]n[/math], которое в свою очередь не превосходит [math]d[/math]. Следовательно, длина [math]BC[/math] не может быть больше [math]d[/math]. [math]\triangleleft[/math]

Алгоритм

Заметим, что параллельные опорные прямые можно провести не через любую пару точек.

Определение:

Точки, через которые можно провести параллельные опорные прямые, будем называть противоположными (англ. antipodal).

Благодаря предыдущей теореме нам нужно рассмотреть только противоположные точки. Задача в том, чтобы рассмотреть их, не перебирая все пары точек.

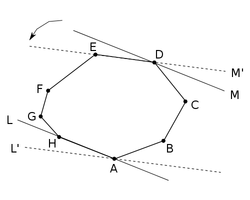
Рассмотрим рисунок справа. [math]L[/math] и [math]M[/math] — опорные прямые, проходящие через вершины [math]A[/math] и [math]D[/math] соответственно. Значит, [math]\langle A,D \rangle[/math] — противоположная пара точек. Если начать вращать прямые против часовой стрелки вокруг данных точек, они будут оставаться опорными прямыми, пока одна из прямых не станет накладываться на сторону многоугольника. В нашем примере, при вращении [math]M[/math] к позиции [math]M'[/math], [math]M[/math] коснётся точки [math]E[/math] раньше, чем [math]L[/math] коснётся [math]B[/math], поэтому [math]\langle A,E \rangle[/math] становится новой парой противоположных точек. Теперь [math]M'[/math] будет вращаться вокруг [math]E[/math], а [math]L'[/math] продолжит вращаться вокруг [math]A[/math], и следующей парой противоположных точек станет [math]\langle B,E \rangle[/math]. Продолжая таким образом, мы сгенерируем все пары противоположных точек, так как параллельные линии пройдут под всеми возможными углами. Определение новой пары противоположных точек требует только одного сравнения углов, которое можно выполнить с помощью предиката поворота.

Ссылки

• M.I. Shamos Computational geometry, 1978 — С. 76.
• Яглом И.М., Болтянский В.Г. Выпуклые фигуры, 1951 — С. 20, 144.
• Реализация - Github.com