Примеры неразрешимых задач: задача о замощении — различия между версиями
Whiplash (обсуждение | вклад) м (→Постановка задачи) |
Whiplash (обсуждение | вклад) |
||
| Строка 22: | Строка 22: | ||
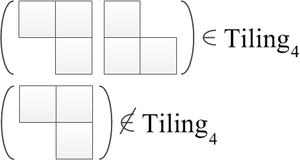
[[file:Tiling_example.png|300px]] | [[file:Tiling_example.png|300px]] | ||
| − | == | + | == Замощение четверти плоскости == |
Пусть даны некоторые типы полимино, причем экземпляров каждого типа дается бесконечно много. | Пусть даны некоторые типы полимино, причем экземпляров каждого типа дается бесконечно много. | ||
Верно ли, что используя любое количество полимино можно полностью замостить без пропусков и выступов четверть плоскости? Поворачивать полимино не разрешено. | Верно ли, что используя любое количество полимино можно полностью замостить без пропусков и выступов четверть плоскости? Поворачивать полимино не разрешено. | ||
| Строка 85: | Строка 85: | ||
}} | }} | ||
| + | == Замощение половины плоскости == | ||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Задача о замощении половины плоскости полимино неразрешима. | ||
| + | |proof= | ||
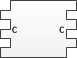
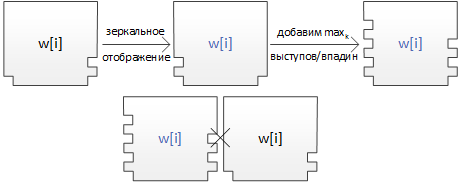
| + | Будем действовать также как и предыдущем доказательстве, только одновременно будем строить еще и зеркально отраженные полимино так, чтобы их нельзя было никак соединить с изначальными. | ||
| + | |||
| + | Например, можно покрасить стороны новых полимино в другой цвет и ввести правило, по которому можно соединять полимино, только если цвета их общей стороны совпадают. | ||
| + | |||
| + | [[Файл:Polyomino_bad_case.png]] | ||
| + | |||
| + | Сделаем так для всех полимино кроме первого ряда. Для него добавим специальное соединение, к которому подходит только зеркально отраженное полимино. | ||
| + | |||
| + | [[Файл:Polyomino_init_2.png]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | == Замощение целой плоскости == | ||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Задача о замощении половины плоскости полимино неразрешима. | ||
| + | |proof= | ||
| + | Аналогично замощению половины плоскости. | ||
| + | }} | ||
== Ссылки == | == Ссылки == | ||
* [http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BB%D0%B8%D0%BC%D0%B8%D0%BD%D0%BE Полимино — Википедия] | * [http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BB%D0%B8%D0%BC%D0%B8%D0%BD%D0%BE Полимино — Википедия] | ||
* [https://www.cs.duke.edu/courses/fall08/cps234/projects/tilings.pdf The tiling problem] | * [https://www.cs.duke.edu/courses/fall08/cps234/projects/tilings.pdf The tiling problem] | ||
* [http://www.univ-orleans.fr/lifo/Members/Nicolas.Ollinger/talks/2008/03/turku.pdf The domino problem] | * [http://www.univ-orleans.fr/lifo/Members/Nicolas.Ollinger/talks/2008/03/turku.pdf The domino problem] | ||
Версия 17:00, 15 января 2014
Содержание
Определения
|
| Определение: |
| Замощение плоскости (tiling) - представление плоскости в виде множества непересекающихся полимино. |
Пусть дана плоскость и набор полимино , если (говорящая по клетке, какому полимино она соответствует) тогда считается, что можно замостить плоскость данным набором.
| Определение: |
| плоскости можно замостить. |
Замощение четверти плоскости
Пусть даны некоторые типы полимино, причем экземпляров каждого типа дается бесконечно много. Верно ли, что используя любое количество полимино можно полностью замостить без пропусков и выступов четверть плоскости? Поворачивать полимино не разрешено.
| Теорема: |
Задача о замощении четверти плоскости полимино неразрешима. |
| Доказательство: |
|
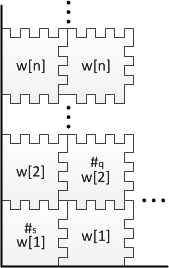
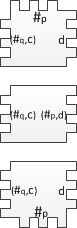
Сведём задачу останова к данной задаче. Пусть дана машина Тьюринга и слово . Требуется определить, остановится ли данная МТ на входе . Будем эмулировать процесс выполнения МТ путем построения вертикальных рядов, каждый из которых эквивалентен конфигурации МТ на определенном этапе выполнения. Первый ряд заполняется начальной конфигурацией, а каждый следующий ряд соответствует следующей конфигурации. Теперь на основе заданной МТ будем строить набор полимино, которые будут иметь следующий вид: На каждой стороне такого полимино находится определенное число выступов/впадин. Каждому символу из алфавита, состоянию и паре из состояния и символа сопоставим некоторое уникальное число (можно ограничить ) – это и будет количество выступов/впадин находящихся на одной стороне полимино.
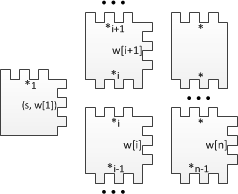
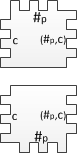
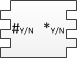
где – уникальные числа для каждых соседних двух полимино из начальной конфигурации. Первое полимино характеризует начальное состояние, последующие за ним кодируют входное слово, и завершающее полимино требуется для корректного замощения оставшейся части ряда. Далее строим полимино для всех элементов алфавита : В нем количество впадин слева равно количеству выступов справа. Такой тип полимино передает содержимое ленты МТ следующему ряду. Теперь построим полимино для функции перехода , где : На рисунке изображены (сверху вниз) полимино соответствующие значениям . Вместе со следующим типом они эмулируют перемещение головки МТ. Далее построим следующий тип полимино: Эти полимино получают на вход символ алфавита от предыдущего ряда и состояние от соседнего полимино, а затем передает следующему ряду пару из состояния и символа.
Такое полимино имеет уникальное число выступов справа. Ни одно другое полимино из полученного набора не сможет к нему присоединиться, и процесс дальнейшего замощения будет невозможен.
Таким образом, четверть плоскости можно замостить тогда и только тогда, когда закодированная МТ не останавливается на данном входе. Иными словами есть бесконечное количество конфигураций, не переходящих в конечное состояние. Это значит, что мы сможем замощать плоскость ряд за рядом бесконечное количество раз, что в результате замостит плоскость. Если же МТ остановится, то и замостить четверть плоскости мы не сможем из-за того, что конечное полимино не имеет продолжения. Значит задача о замощении полимино не разрешима. |
Замощение половины плоскости
Замощение целой плоскости
| Теорема: |
Задача о замощении половины плоскости полимино неразрешима. |
| Доказательство: |
| Аналогично замощению половины плоскости. |