Триангуляция Делоне — различия между версиями
Yulya3102 (обсуждение | вклад) (→Динамическая триангуляция) |
Yulya3102 (обсуждение | вклад) м (→Существование триангуляции Делоне) |
||
| Строка 63: | Строка 63: | ||
</tex> | </tex> | ||
| − | Из определителя видно, что, если <tex>t > 1</tex> (точка <tex>x</tex> лежит вне окружности), то определитель положителен, то есть точка <tex>x</tex> лежит выше плоскости, заданной точками <tex>\{a_i\}</tex>. Если же <tex>t < 1</tex> (точка <tex>x</tex> лежит внутри окружности), то определитель отрицателен, и точка <tex>x</tex> лежит ниже плоскости. Если же точка лежит на окружности, то она попадает на ту же плоскость. | + | Из определителя видно, что знак определителя зависит от ориентации исходных точек <tex>\{a_i\}</tex> и от знака <tex>t^2-1</tex>. Для определённости будем считать, что точки <tex>\{a_i\}</tex> ориентированы так, что предикат поворота положителен. Тогда если <tex>t > 1</tex> (точка <tex>x</tex> лежит вне окружности), то определитель положителен, то есть точка <tex>x</tex> лежит выше плоскости, заданной точками <tex>\{a_i\}</tex>. Если же <tex>t < 1</tex> (точка <tex>x</tex> лежит внутри окружности), то определитель отрицателен, и точка <tex>x</tex> лежит ниже плоскости. Если же точка лежит на окружности, то она попадает на ту же плоскость. |
}} | }} | ||
{{Теорема | {{Теорема | ||
| Строка 73: | Строка 73: | ||
Из единственности выпуклой оболочки следует, что такое подразбиение единственно. | Из единственности выпуклой оболочки следует, что такое подразбиение единственно. | ||
}} | }} | ||
| + | |||
== Критерий Делоне для рёбер == | == Критерий Делоне для рёбер == | ||
{{Определение | {{Определение | ||
Версия 01:12, 14 февраля 2014
| Конспект написан не до конца, но основные вещи уже есть. |
| НЯ! Эта статья полна любви и обожания. Возможно, стоит добавить ещё больше? |
Содержание
Определение
| Определение: |
| Подразбиение Делоне — такое разбиение плоскости на множество выпуклых фигур, что в окружности, описанной вокруг любой из фигур, не находится никаких точек. |
| Определение: |
| Триангуляция Делоне — триангуляция, являющаяся подразбиением Делоне. |
Существование триангуляции Делоне
| Лемма: |
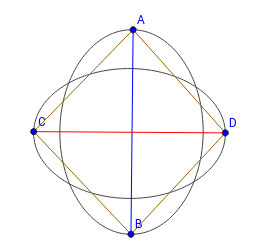
Окружность, спроецированная на параболоид, находится в одной плоскости. Все точки, лежащие внутри окружности, будут лежать под этой плоскостью. Точки, лежащие вне окружности, будут лежать над плоскостью. |
| Доказательство: |
|
Докажем данное утверждение для n-мерного случая. Возьмём афинно независимых точек и опишем вокруг них окружность с центром в точке и радиусом . Возьмём произвольную точку , лежащую на расстоянии от , и посмотрим, как параметр влияет на положение её проекции на параболоид. Представим как , а — как . Тогда проекции точек на параболоид будут выглядеть так:
Так как афинно независимы, то можно представить как , причём . Запишем определитель, показывающий положение точки на параболоиде относительно плоскости, заданной точками :
Умножим первые строк на и вычтем из последней: Из определителя видно, что знак определителя зависит от ориентации исходных точек и от знака . Для определённости будем считать, что точки ориентированы так, что предикат поворота положителен. Тогда если (точка лежит вне окружности), то определитель положителен, то есть точка лежит выше плоскости, заданной точками . Если же (точка лежит внутри окружности), то определитель отрицателен, и точка лежит ниже плоскости. Если же точка лежит на окружности, то она попадает на ту же плоскость. |
| Теорема: |
Подразбиение Делоне существует, причём для каждого набора точек оно единственно. |
| Доказательство: |
|
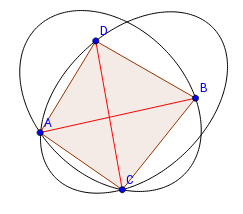
Спроецируем все точки на параболоид и построим выпуклую оболочку. По лемме очевидно, что внутри окружностей, описанных вокруг проекций граней выпуклой оболочки, не будет лежать никаких точек. Значит, проекции граней — фигуры подразбиения Делоне. Значит, такое подразбиение существует. Из единственности выпуклой оболочки следует, что такое подразбиение единственно. |
Критерий Делоне для рёбер
| Определение: |
| Критерий Делоне для ребра: на ребре можно построить такую окружность, что внутри неё не будет лежать никаких точек. |
| Лемма: |
Триангуляции Делоне принадлежат те и только те рёбра (с поправкой на точки, лежащие на одной окружности), которые удовлетворяют критерию Делоне. |
| Доказательство: |
|
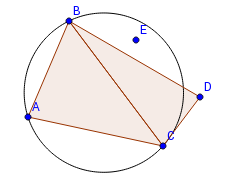
То, что для рёбер, принадлежащих триангуляции Делоне, выполняется критерий Делоне для рёбер, очевидно (вокруг каждого ребра можно описать окружность, проходящую через противолежащую ему точку в смежном треугольнике, причём в окружности не будет никаких точек по критерию Делоне). Докажем, что если для ребра выполняется критерий Делоне, то оно принадлежит триангуляции Делоне. Предположим, что это ребро (назовём его ) не принадлежит триангуляции Делоне. Тогда существует пересекающее его ребро , принадлежащее триангуляции. Рассмотрим четырёхугольник . Точки и лежат вне окружности, построенной на как на хорде, поэтому сумма углов и меньше 180°. Аналогичным образом доказывается, что сумма углов и тоже меньше 180°. Значит, сумма углов четырёхугольника меньше 360°, что невозможно. Противоречие. Значит, ребро принадлежит триангуляции Делоне. |
Динамическая триангуляция
| Определение: |
| Ребро назовём хорошим, если для пары треугольников, которым принадлежит это ребро, выполняется критерий Делоне (то есть вершина, противолежащая ребру в одном треугольнике, не лежит в окружности, описанной вокруг другого, и наоборот) |
| Лемма: |
Из двух рёбер, которые можно провести для пары треугольников, как минимум одно хорошее. |
| Доказательство: |
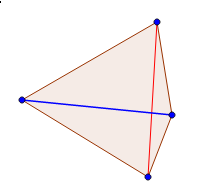
| Предположим, что это не так, то есть оба ребра (назовём их и ) плохие. Рассмотрим четырёхугольник и окружность, описанную вокруг треугольника . Точка лежит внутри этой окружности, значит, сумма углов и больше 180°. Аналогично доказывается, что сумма углов и больше 180°. Значит, сумма углов четырёхугольника больше 360°, что невозможно. |
| Лемма: |
Если все рёбра хорошие, то и триангуляция хорошая. |
| Доказательство: |
| Предположим, что это не так, то есть все рёбра хорошие, но существует треугольник, описанная окружность которого содержит какие-либо точки триангуляции. Рассмотрим ребро (пусть это будет ), отрезающее сегмент, содержащий точки, и выберем из этих точек такую точку , что угол максимален. Так как угол максимален, то точка является вершиной смежного с треугольника (в противном случае в треугольнике будут лежать какие-либо точки, что невозможно по построению). Значит, ребро плохое, что противоречит условию. Значит, предположение неверно. |
| Определение: |
| Для пары смежных треугольников flip — убирание смежного ребра и проведение другого. |
Из леммы следует, что если ребро плохое, то флип сделает его хорошим.
| Лемма: |
Флипами можно достичь хорошей триангуляции за конечное время. |
| Доказательство: |
| Очевидно, потому что каждый флип уменьшает разность объёмов параболоида и триангуляции, спроецированной на него. |
Вставка точки
Вставка точки, лежащей внутри триангуляции
Для начала локализуемся: поймём, в каком фейсе лежит точка (или на каком ребре).
Если точка лежит внутри фейса, добавляем три ребра, сам фейс превращаем в один из новых смежных с вставляемой точкой и добавялем ещё два фейса.
Если же точка лежит на ребре, два смежных с ребром фейса превращаем в два новых, добавляем ещё два, а так же превращаем ребро, на которое вставляется точка, в ребро, которое заканчивается в этой точке, и вставляем три новых.
Итого у нас появилось несколько новых рёбер. Они все хорошие ( TODO: Доказать, почему), плохими могут оказаться только рёбра, противолежащие вставленной точке. Флипаем рёбра, пока триангуляция не станет хорошей.
Среднее число флипов — ( TODO: Доказать, почему). Поэтому время вставки целиком зависит от времени локализации.
Вставка точки, лежащей снаружи триангуляции
Представим, что вне триангуляции — бесконечные треугольники, основания которых — рёбра выпуклой оболочки триангуляции, а противолежащая ребру вершина — это бесконечно удалённая точка. Тогда понятно, что вставка точки, не лежащей в триангуляции, сведётся к вставке точки внутрь триангуляции, если мы научимся обрабатывать бесконечные фейсы.
TODO: Написать про бесконечно удалённую точку
Удаление точки
При удалении точки получится звёздный многоугольник, который можно затриангулировать за линию. Дальше по традиции флипаем всё, что могло стать плохим, пока не получим хорошую триангуляцию.
Средняя степень вершины в триангуляции — ( TODO: Почему? — почти то, что нужно, здесь [1]. Потом пишем , делим на и получаем ), поэтому триангуляция звёздного многоугольника будет тоже за . С флипами всё тоже, в общем-то, хорошо. Итого удаление точки работает за .
Локализационная структура
Сама структура
В общем-то, довольно стандартная схема для рандомизированных структур: на нижнем уровне содержатся все точки; каждая точка с вероятностью p проходит на следующий уровень.
Локализация
Как происходит локализация: нам дают точку , которая на предыдущем уровне была ближайшей к точке , которую мы локализуем. Нужно получить следующую точку , которая будет ближайшей уже на этом уровне. Делается это следующим образом:
- Находим, в каком из треугольников, смежных с , лежит отрезок
- Находим, какие рёбра треугольников пересекает , в итоге находим треугольник, в котором лежит
- Находим ближайшую к точку. Первым кандидатом на то, чтобы быть ближайшей точкой, становится ближайшая к вершина найденного в предыдущем пункте треугольника. Для каждого кандидата нужно просмотреть смежные вершины в поиске точки, которая находится ближе к — эта точка становится следующим кандидатом. Если же среди соседей точки не нашлось более близких, значит, эта точка и есть ближайшая.
Корректность алгоритма
| Теорема: |
Данный алгоритм найдёт ближайшую точку. |
| Доказательство: |
|
TODO: Картинку для ясности Предположим, что это не так. Назовём локализуемую точку , а последнего кандидата на то, чтобы быть ближайшей точкой — . Раз эта точка на самом деле не ближайшая, то в окружности, проходящей через , с центром в точке найдутся ещё какие-то точки, не смежные с . Рассмотрим ближайшую из них к : точку . Построим на окружность как на диаметре. В этой окружности не будет лежать никаких точек, так как мы взяли ближайшую. Значит, ребро удовлетворяет критерию Делоне и должно являться ребром триангуляции, но по предположению этого ребра нет. Значит, предположение неверно. |
Профит
TODO: Время работы, требуемая память
Constraints
| Определение: |
| Констрейнты — рёбра, которые нельзя флипать |
| Утверждение: |
Хорошая триангуляция с констрейнтом может быть хорошей с точностью до видимости через констрейнт |
Вставка
Смотрим на список рёбер, пересечённых ещё не вставленным констрейнтом ( TODO: Картинку бы), и флипаем их. Последнее флипнутое ребро и будет констрейнтом (по понятным причинам), после флипа пометим его как констрейнт. Понятное дело, критерий «хорошести» ребра при таких фокусах немного изменится: туда добавится проверка на то, не является ли ребро констрейнтом. Затем флипаем всё, что могло стать плохим (кроме констрейнта), пока триангуляция вновь не станет условно хорошей.
TODO: Тут должно быть ещё несколько упоительных фактов про то, что вставка производится за , где — число пересечённых рёбер, и про то, что, если флипать что попало, можно нарваться на флип в невыпуклом многоугольнике
Удаление
Аналогично: помечаем ребро как не-констрейнт и начинаем флипать, пока не дойдём до хорошей (или условно хорошей) триангуляции.
Работает оно столько же, сколько и вставка, ибо всё, что мы нафлипали при вставке, нужно перефлипать обратно.
Констрейнты в локализационной структуре
В локализационную структуру констрейнты нужно вставлять только на нижний уровень, ибо выше они нафиг не нужны.