Пересечение полуплоскостей, связь с выпуклыми оболочками — различия между версиями
Igorjan94 (обсуждение | вклад) |
Igorjan94 (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство {{---}} Пересечение выпуклых фигур выпукло, а полуплоскоть выпукла) | Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство {{---}} Пересечение выпуклых фигур выпукло, а полуплоскоть выпукла) | ||
| − | Рассмотри отображение <tex> D </tex> между точками и прямыми: | + | Рассмотри отображение <tex> D </tex> между точками и прямыми, такое что: |
<tex> D(P(k, b)) = (Y = kX - b) </tex> | <tex> D(P(k, b)) = (Y = kX - b) </tex> | ||
| Строка 11: | Строка 11: | ||
<tex> D(Y = kX + b) = P(k, -b) </tex> | <tex> D(Y = kX + b) = P(k, -b) </tex> | ||
| − | <tex> | + | Обозначим <tex> L = {l_1, l_2, ... , l_n} </tex> {{---}} множество прямых. |
| − | |||
Замечания: | Замечания: | ||
| − | * Точка <tex> p </tex> лежит на прямой <tex> p </tex> | + | * <tex> D(D(P)) = P </tex> |
| + | * Точка <tex> p </tex> лежит на прямой <tex> l_i </tex> тогда и только тогда, когда <tex> D(l_i) </tex> лежит на прямой <tex> D(p) </tex>. | ||
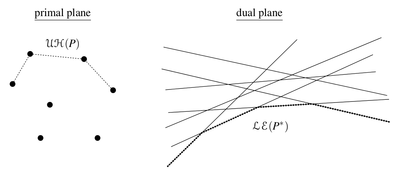
| + | * Точка <tex> p </tex> лежит на прямой-границе пересечения <tex> l_i </tex> тогда и только тогда, когда <tex> D(l_i) </tex> {{---}} экстремальная точка <tex> D(L) </tex>. | ||
| + | * Точка <tex> l_i </tex> вершина пересечения прямых <tex> l_i </tex> и <tex> l_j </tex> тогда и только тогда, когда <tex> l(D(l_i), D(l_j)) </tex> {{---}}опорное ребро конвекс халла <tex> CH(D(L)) </tex> | ||
* | * | ||
| − | |||
| − | |||
== Источники == | == Источники == | ||
* Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 15 page 253-254 | * Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 15 page 253-254 | ||
Версия 15:37, 21 февраля 2014
Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто.
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство — Пересечение выпуклых фигур выпукло, а полуплоскоть выпукла)
Рассмотри отображение между точками и прямыми, такое что:
Обозначим — множество прямых.
Замечания:
- Точка лежит на прямой тогда и только тогда, когда лежит на прямой .
- Точка лежит на прямой-границе пересечения тогда и только тогда, когда — экстремальная точка .
- Точка вершина пересечения прямых и тогда и только тогда, когда —опорное ребро конвекс халла
Источники
- Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 15 page 253-254
- http://wwwisg.cs.uni-magdeburg.de/ag/lehre/SS2012/GAG/slides/V12.pdf