Пересечение полуплоскостей, связь с выпуклыми оболочками — различия между версиями
Igorjan94 (обсуждение | вклад) м |
Igorjan94 (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
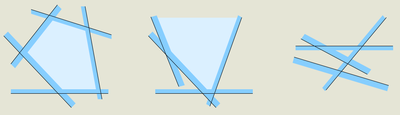
[[Файл:samplesHalfspaces.png|400px|thumb|right|Пересечение существует и выпукло, неограничено или пусто]] | [[Файл:samplesHalfspaces.png|400px|thumb|right|Пересечение существует и выпукло, неограничено или пусто]] | ||
| − | |||
Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто. | Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто. | ||
| Строка 6: | Строка 5: | ||
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство {{---}} Пересечение выпуклых фигур выпукло, а полуплоскость выпукла) | Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство {{---}} Пересечение выпуклых фигур выпукло, а полуплоскость выпукла) | ||
| − | Пусть | + | Пусть полуплоскости заданы уравнениями прямых и ориентацией, с какой стороны от прямой лежит полуплоскость. |
| + | |||
| + | Сначала рассмотрим все полуплоскости, которые "смотрят", то есть ориентированны, вниз. Аналогично можно рассмотреть все полуплоскости, которые ориентированны вверх. | ||
| + | |||
| + | {{Лемма | ||
| + | |statement= | ||
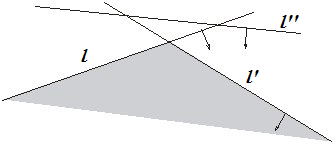
| + | [[Файл:halfSpaces.png|400px|thumb|right|Нужна ли полуплоскость <tex> l'' </tex>?]] | ||
| + | Предикат проверки (см. рисунок) того, что прямая <tex> l'' : A''x + B''y + C'' = 0 </tex> лежит над пересечением прямых <tex> l : Ax + By + C = 0 </tex> и <tex> l' : A'x + B'y + C' = 0 </tex> равен знаку определителя <tex> | ||
\begin{vmatrix} | \begin{vmatrix} | ||
A & B & C \\ | A & B & C \\ | ||
| Строка 13: | Строка 19: | ||
\end{vmatrix} | \end{vmatrix} | ||
</tex>. | </tex>. | ||
| − | + | |proof= | |
| − | + | Для проверки предиката нужно определить знак выражения <tex> A''x_0 + B''y_0 + C'' </tex>, где <tex> (x_0, y_0) </tex> {{---}} точка пересечения прямых <tex> l' </tex> и <tex> l </tex>. Эту точку находится из уравнения <tex> \begin{pmatrix} | |
A & B\\ | A & B\\ | ||
A' & B' | A' & B' | ||
| Строка 46: | Строка 52: | ||
\end{vmatrix} | \end{vmatrix} | ||
} | } | ||
| − | </tex>. Подставим | + | </tex>. Подставим это решение в <tex> A''x_0 + B''y_0 + C'' </tex> и домножим на определитель. |
<tex> A'' (B'; -B)(-C; -C') + B'' (-A'; A)(-C; -C') + C \begin{vmatrix} A & B \\ A' & B' \end{vmatrix} = A'' \begin{vmatrix} B' & B \\ -C' & -C \end{vmatrix} - B'' \begin{vmatrix} A' & A \\ -C' & -C \end{vmatrix} + C'' \begin{vmatrix} A & A' \\ B & B' \end{vmatrix} = \begin{vmatrix} A'' & A' & A \\ B'' & B' & B \\ -C'' & -C' & -C \end{vmatrix} = \begin{vmatrix} A & B & C \\ | <tex> A'' (B'; -B)(-C; -C') + B'' (-A'; A)(-C; -C') + C \begin{vmatrix} A & B \\ A' & B' \end{vmatrix} = A'' \begin{vmatrix} B' & B \\ -C' & -C \end{vmatrix} - B'' \begin{vmatrix} A' & A \\ -C' & -C \end{vmatrix} + C'' \begin{vmatrix} A & A' \\ B & B' \end{vmatrix} = \begin{vmatrix} A'' & A' & A \\ B'' & B' & B \\ -C'' & -C' & -C \end{vmatrix} = \begin{vmatrix} A & B & C \\ | ||
A' & B' & C' \\ | A' & B' & C' \\ | ||
A'' & B'' & C'' \end{vmatrix} </tex> | A'' & B'' & C'' \end{vmatrix} </tex> | ||
| + | }} | ||
Таким образом если представить прямую <tex> Ax + By + C = 0 </tex> как точку с координатами <tex> (A, B, C) </tex>, где <tex> C </tex> {{---}} однородная координата, то этот предикат {{---}} всего лишь поворот, а проверка предиката {{---}} проверка очередной точки в [[Статические выпуклые оболочки: Джарвис, Грэхем, Эндрю, Чен, QuickHull#Алгоритм Грэхема|обходе Грэхема]] для нахождения выпуклой оболочки. | Таким образом если представить прямую <tex> Ax + By + C = 0 </tex> как точку с координатами <tex> (A, B, C) </tex>, где <tex> C </tex> {{---}} однородная координата, то этот предикат {{---}} всего лишь поворот, а проверка предиката {{---}} проверка очередной точки в [[Статические выпуклые оболочки: Джарвис, Грэхем, Эндрю, Чен, QuickHull#Алгоритм Грэхема|обходе Грэхема]] для нахождения выпуклой оболочки. | ||
| Строка 57: | Строка 64: | ||
* Отсортировать все полуплоскости по углу наклона; | * Отсортировать все полуплоскости по углу наклона; | ||
* Запустить обход Грэхема для полуплоскостей, смотрящих вниз (с предикатом-определителем); | * Запустить обход Грэхема для полуплоскостей, смотрящих вниз (с предикатом-определителем); | ||
| − | * | + | * Запустить обход Грэхема для полуплоскостей, смотрящих вверх; |
* Пересечь две цепочки. | * Пересечь две цепочки. | ||
| Строка 63: | Строка 70: | ||
== Источники == | == Источники == | ||
| − | |||
* http://wwwisg.cs.uni-magdeburg.de/ag/lehre/SS2012/GAG/slides/V12.pdf | * http://wwwisg.cs.uni-magdeburg.de/ag/lehre/SS2012/GAG/slides/V12.pdf | ||
[[Категория: Вычислительная геометрия]] | [[Категория: Вычислительная геометрия]] | ||
Версия 21:33, 9 февраля 2015
Задача: есть конечное множество полуплоскотей, найти фигуру их пересечения или сообщить что оно пусто.
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство — Пересечение выпуклых фигур выпукло, а полуплоскость выпукла)
Пусть полуплоскости заданы уравнениями прямых и ориентацией, с какой стороны от прямой лежит полуплоскость.
Сначала рассмотрим все полуплоскости, которые "смотрят", то есть ориентированны, вниз. Аналогично можно рассмотреть все полуплоскости, которые ориентированны вверх.
| Лемма: |
| Доказательство: |
|
Для проверки предиката нужно определить знак выражения , где — точка пересечения прямых и . Эту точку находится из уравнения . Решением будет . Подставим это решение в и домножим на определитель. |
Таким образом если представить прямую как точку с координатами , где — однородная координата, то этот предикат — всего лишь поворот, а проверка предиката — проверка очередной точки в обходе Грэхема для нахождения выпуклой оболочки.
Алгоритм:
- Отсортировать все полуплоскости по углу наклона;
- Запустить обход Грэхема для полуплоскостей, смотрящих вниз (с предикатом-определителем);
- Запустить обход Грэхема для полуплоскостей, смотрящих вверх;
- Пересечь две цепочки.
От пересечения цепочек напрямую зависит фигура пересечения: неограниченная область получается если одна из цепочек пуста, а ограниченная — когда обе цепочки не пусты и пересекаются.