Обсуждение участника:SergeyBud — различия между версиями
SergeyBud (обсуждение | вклад) |
SergeyBud (обсуждение | вклад) |
||
| Строка 6: | Строка 6: | ||
==Устройство HAT== | ==Устройство HAT== | ||
| − | HAT состоит из главного массива указателей и ряда листьев(так же одномерные массивы, в которых хранятся элементы. | + | [[Файл:AlgoF2.gif|right]] |
| − | + | HAT состоит из главного массива указателей и ряда листьев(так же одномерные массивы), в которых хранятся элементы. | |
| + | Число указателей в главном массиве и число элементов в каждом листе - равны между собой, и являются степенями двойки. | ||
| + | |||
| + | =Добавление элементов= | ||
| + | Благодаря степеням двойки, мы сможем эффективно находить элементы в HAT, используя поразрядные операции(см.Пример1). Чаще всего при добалении элемента, в одном из листьев(последний незаполненный на данный момент) найдется свободное место, что позволит осуществить быструю вставку(O(1)). | ||
| + | Реже мы столкнемся со случаем, когда необходимо создать новый лист. Необходимо всего лишь добавить указатель в свободную ячейку главного массива, а значит также сможем произвести вставку элемента за О(1). | ||
Версия 12:22, 1 июня 2014
HAT(Hashed Array Tree) — структура данных, объединяющая в себе некоторые возможности массивов, хэш-таблиц и деревьев.
Значимость
Массивы переменной длины - наиболее естественная и удобная структура данных для многих приложений, так как они обеспечивают постоянное время доступа к их элементам. Однако при реализации мы можем столкнуться с двумя основными проблемами: черезмерое копирование элементов и использование памяти. Для примера рассмотрим однку из реализаций: /*****/
Устройство HAT
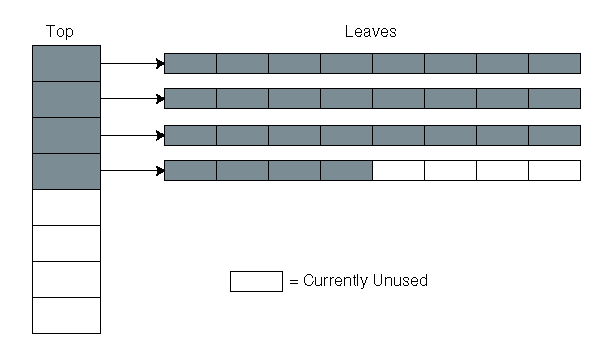
HAT состоит из главного массива указателей и ряда листьев(так же одномерные массивы), в которых хранятся элементы. Число указателей в главном массиве и число элементов в каждом листе - равны между собой, и являются степенями двойки.
Добавление элементов
Благодаря степеням двойки, мы сможем эффективно находить элементы в HAT, используя поразрядные операции(см.Пример1). Чаще всего при добалении элемента, в одном из листьев(последний незаполненный на данный момент) найдется свободное место, что позволит осуществить быструю вставку(O(1)). Реже мы столкнемся со случаем, когда необходимо создать новый лист. Необходимо всего лишь добавить указатель в свободную ячейку главного массива, а значит также сможем произвести вставку элемента за О(1).