Матроид Вамоса

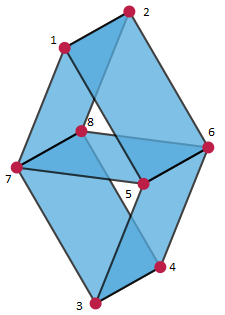
Матроид Вамоса или куб Вамоса — это матроид над восьми элементным множеством, который не изоморфен матричному ни над каким полем. Он назван в честь английского математика Питера Вамоса (Peter Vámos), который первым описал его в неопубликованной рукописи в 1968.

Задание матроида

Пусть [math] E = \{1, 2, 3, 4, 5, 6, 7, 8\}[/math]. Матроид Вамоса [math]V[/math] удобно задать, назвав все его зависимые множества: это все подмножества [math]E[/math], в которых не менее пяти элементов, а также [math]\{1, 2, 5, 6\}, \{1, 2, 7, 8\}, \{3, 4, 5, 6\}, \{3, 4, 7, 8\}, \{5, 6, 7, 8\}[/math].

Доказательство матроидной природы

Сначала убедимся в том, что перед нами действительно матроид. Фактически нуждается в проверке лишь тот факт, что если [math]A[/math] и [math]B[/math] независимые множества и [math]|B| = 3[/math], [math]|A| = 4[/math], то в [math]A[/math] найдется такой элемент [math]e[/math], что [math]B \cup \{e\}[/math] — независимое множество. Когда [math]B \subset A[/math], это очевидно. В противном же случае множество [math] A \setminus B[/math] содержит по меньшей мере два различных элемента. Обозначим их через [math]e1[/math] и [math]e2[/math]. Теперь осталось заметить, что из множеств [math]B \cup \{e1\}[/math] и [math]B \cup \{e2\}[/math] хотя бы одно независимое, так как по условию нет двух зависимых множеств из четырtх элементов, отличающихся одним элементом.