Алгоритм Ландау-Вишкина (k несовпадений)

Постановка задачи: Дано число [math]k \gt 0[/math] текст [math]y[1...n][/math] и образец [math]x[1...m][/math], [math]m \lt n[/math]. Требуется найти все подстроки текста длины [math]m[/math], с не более чем [math]k[/math] несовпадающими символами с образцом. Эту задачу решает алгоритм Ландау-Вишкина (k несовпадений) (англ.Landau-Vishkin Algorithm)

Алгоритм

Идея

В таблицу tm по номеру несовпадения записывается соответстующий индекс образца, то есть [math]tm[i][1] = a[/math], [math]tm[i][2] = b[/math], [math]tm[i][3] = c[/math] и т д.

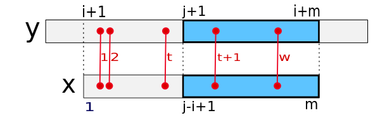
При анализе используется двумерный массив несовпадений текста [math]tm[0...n-m][1...k+1][/math], содержащий информацию о несовпадениях текста с образцом. По завершении анализа в его [math]i[/math]-й строке содержатся позиции в [math]x[/math] первых [math]k+1[/math] несовпадений между строками [math]x[1...m][/math] и [math]y[i+1...i+m][/math]. Таким образом, если [math]tm[i][v] = s[/math], то [math]y[i+s] \neq x[s][/math], и это [math]v[/math]-е несовпадение между [math]x[1...m][/math] и [math]y[i+1...i+m][/math], считая слева направо. Если число [math]d[/math] несовпадений [math]x[1...m][/math] с подстрокой [math]y[i+1...i+m][/math] меньше [math]k+1[/math], то, начиная с [math]d+1[/math], элементы [math]i[/math]-й строки равны значению по умолчанию [math]m+1[/math].

Заметим, если [math]tm[i][k+1] = m+1[/math], то подстрока [math]y[i+1...i+m][/math] отличается от образца [math]x[/math] не более, чем на [math]k[/math] символов, и, таким образом, является решением задачи.

Затем образец сканируется параллельно с текстом слева на права по одному символу за раз. На итерации [math]i[/math] с образцом сравнивается подстрока [math]y[i+1...i+m][/math]. [math]j[/math] - обозначим самую правую позицию в тексте, достигнутую за предыдущие итерации, то есть [math]j[/math] является максимальным из чисел [math]r+tm[r, k + 1][/math], где [math]0 \leqslant r \lt i[/math]. Если [math]i \lt j[/math], в [math]b[/math] присваивается результат работы [math]merge[/math], которая находит количество несовпадений между [math]x[1... j-i][/math] и [math]y[i+1...j][/math]. Если [math]b[/math] не превышает [math]k[/math], вызывается процедура [math]extend[/math], которая сравнивает подстроки [math]y[j + 1...i + m][/math] и [math]x[j - i + 1...m][/math], где изменяется таблица текстовых несовпадений. Переменная [math]r[/math] будет рассмотренна ниже.

tm[0...n-m][1...k+1] = m+1 // инициализация r = 0 j = 0 for i = 0 to n - m b = 0 if i < j b = merge(i, r, j) if b < k + 1 r = i extend(i, j, b)

Процедура extend

Синие подстроки сравниваются в процедуре extend. [math]w \lt k + 1[/math]

Рассмотрим процедуру [math]extend[/math] подробнее. Она сравнивает подстроки [math]y[j + 1...i + m][/math] и [math]x[j - i + 1...m][/math], в случае несовпадения [math]b[/math] увеличивается и таблица текстовых несовпадений обновляется. Это происходит пока либо не будет найдено [math]k + 1[/math] несовпадений (учитывая несовпадения, которые были найдены раньше на [math]i[/math]-ой итерации), либо не будет достигнуто [math]y[i+m][/math] с не больше чем [math]k[/math] несовпадениями, то есть найдено вхождение образца, начинающееся с [math]y[i+1][/math].

extend(i, j, b) while (b < k + 1) and (j - i < m) j++ if y[j] != x[j-1] b++ tm[i][b] = j - i

Процедура merge

Синие подстроки сравниваются в процедуре merge. Красным отмечены несовпадения.

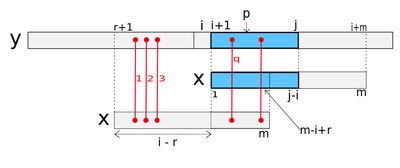
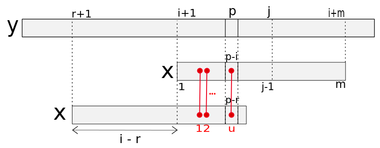
Рассмотрим процедуру [math]merge[/math] подробнее. Она находит количество несовпадений между [math]x[1... j-i][/math] и [math]y[i+1...j][/math] и устанавливает b равным найденному числу, при этом используется полученая ранее информация. Введем [math]r[/math] - это строка таблицы несовпадений, в которой есть информация о несовпадениях, полученных при совмещении начала образца и [math]y[r+1][/math]. [math]r+tm[r][k+1][/math] содержит текущий номер самой правой из проверенных на настоящий момент позиций текста. Поэтому при обработки построки начинающейся с [math]y[i+1][/math], можно учитывать информацию в [math]r[/math]-ой строке [math]tm[/math], которая содержит информацию о сопоставлении образца с [math]y[i][/math]. Подходящими значениями из таблицы несовпадений являются, таким образом, [math]tm[r][q ... k+1][/math], где [math]q[/math] – это наименьшее из целых чисел, для которых [math]r+tm[r][q] \gt i[/math]. Однако, следует учитывать тот факт, что эти несовпадения соответствуют началу образца, выравниваемому с [math]y[r+1][/math], в то время как текущая позиция образца выровнена с [math]y[i+1][/math] – разница в [math]i - r[/math] мест.

В таблицу pm по номеру несовпадения записывается соответстующий индекс верхнего образца, то есть [math]pm[i][1] = a[/math], [math]pm[i][2] = b[/math], [math]pm[i][3] = c[/math] и т д.

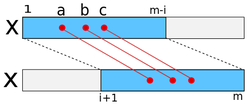
Также в алгоритме используется двумерный массив несовпадений образца [math]pm[1...m-1][1...2k+1][/math], генерируемой на стадии предварительной обработки образца. В нем содержатся позиции несовпадения образца с самим собой при различных сдвигах, аналогично [math]tm[/math], то есть в [math]i[/math]-ой строке содержитатся позиции внутри [math]x[/math] первых [math]2k+1[/math] несовпадений между подстроками [math]x[1...m-i][/math] и [math]x[i+1...m][/math]. Таким образом, если [math]pm[i, v] = s[/math], то [math]x[i+s] \neq x[s][/math], и это [math]v[/math]-е несовпадение между [math]x(1, m-i)[/math] и [math]x(i+1, m)[/math] слева направо. Если число [math]d[/math] несовпадений между этими строками меньше [math]2k+1[/math], то, начиная с [math]d+1[/math], элементы [math]i[/math]-й строки равны [math]m+1[/math], значению по умолчанию. Построение [math]tm[/math] будет подробнее рассмотренно позднее.

Таким образом, для [math]merge[/math] интерес представляет строка [math]i - r[/math] таблицы несовпадений образца, причем используются значения [math]pm[i-r][1...t][/math], где [math]t[/math] – самое правое несовпадение в [math]pm[i-r][1...2k+1][/math], такое, что [math]pm[i-r][t] \lt j-i+1[/math], так как требуются только несовпадения в подстроке [math]x[1...j-i][/math].

Чтобы использовать упомянутую информацию в процедуре [math]merge[/math], рассмотрим в тексте позицию [math]p[/math], находящуюся в диапазоне, [math]i+1 \lt p \lt j[/math] //todo. Рассмотрим следующие условия для позиции [math]p[/math]:

Условие A: когда символы [math]x[1][/math] и [math]y[r+1][/math] совмещены, позиция [math]p[/math] в тексте соответствует предварительно выявленному несовпадению между образцом и текстом, то есть [math]y[p] \neq x[p-r][/math], и это несовпадение номер [math]v[/math], где [math]q \lt v \lt k+1[/math], то есть [math]p - r = tm[r][v][/math].

Условие B: для двух копий образца, со сдвигом относительно друг друга [math]i - r[/math], совмещенных с текстом так, что их начальные символы лежат, соответственно, над [math]y[r+1][/math] и [math]y[i+1][/math], позиция [math]p[/math] соответствует несовпадению между двумя образцам, то есть [math]x[p-r] \neq x[p-i][/math]. Это [math]u[/math]-е несовпадение при этом сдвиге, где [math]1 \lt u \lt t[/math], то есть [math]p-i[/math] = [math]pm[i-r][u][/math].

Вспомним, что нас интересует, совпадает ли символ текста в позиции [math]p[/math] с соответствующими символом образца, когда [math]x[1][/math] совмещен с [math]y[i+1][/math], то есть верно ли, что [math]y[p] = x[p-i][/math]. Рассмотрим этот вопрос при разных комбинациях указанных выше условий.

Случай 1: !A and !B: То есть, [math]y[p] = x[p-r][/math] и [math]x[p-r] = x[p-i][/math], откуда [math]y[p] = x[p-i][/math]. Нет необходимости сравнивать символ текста с символом образца, так как ясно, что в этой позиции они совпадают.

Случай 2: (A and !B) or (!A and B): В любом случае [math]y[p] \neq x[p-i][/math] (если лишь условие [math]A[/math] истинно, то [math]y[p] \neq x[p-r][/math] и [math]x[p-r] = x[p-i][/math], откуда [math]y[p] \neq x[p-i][/math], с другой стороны, если выполнено только условие [math]B[/math], то [math]y[p] = x[p-r][/math] и [math]x[p-r] \neq x[p-i][/math], и опять, [math]y[p] \neq x[p-i][/math]). Как и в предыдущем случае, нет необходимости сравнивать символ текста с символом образца, так как известно, что они не совпадают.

Случай 3: A and B: В этом случае мы ничего не можем сказать о том, совпадают ли символы [math]y[p][/math] и [math]x[p-i][/math], поэтому их надо сравнить.

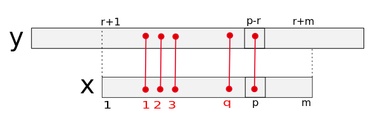
Возвращаемся к процедуре merge. В случае 2, или если в случае 3 выявлено несовпадение символов, необходимо увеличить количество несовпадений символов [math]b[/math] на единицу и обновить [math]tm[i][b][/math]. Соответствующими значениями таблицы для [math]merge[/math] являются [math]tm[i-r][1...t][/math] и [math]tm[r][q...k+1][/math]. Переменные [math]u[/math] и [math]v[/math] в начале устанавливаются равными индексам первых элементов этих двух массовов, соответственно, и последовательно увеличиваются.

Условия окончания работы процедуры следующие:

• Eсли [math]b = k+1[/math], то для случая, когда образц расположен относительно текста так, что [math]x[1][/math] совмещен с [math]y[i+1][/math], обнаружено [math]k+1[/math] несовпадение, поэтому из процедуры можно выйти.

• Bспомним, что самая правая из интересующих нас позиций в [math]merge[/math], а именно, [math]j[/math], равна [math]r+tm[r][k+1][/math], если [math]v = k+2[/math], поэтому [math]tm[r][k+1][/math] будет уже использовано для предыдущего значения [math]v[/math], а именно, [math]v = k+1[/math], и поэтому позиция [math]j[/math] должна быть пропущена. Следовательно, в этом случае также можно выйти из процедуры.

• Процедуру можно прервать, если [math]i+pm[i-r][u] \gt j[/math] и [math]tm[r][v] = m+1[/math]. Если выполняется вторая часть этого условия, то [math]r+tm[r][v][/math] равняется [math]j[/math], и соответствует суммам для последующих значений [math]v[/math] вплоть до [math]k+1[/math]. В этом случае процедура может быть прервана, если выполняется также первая часть приведенного условия, так как она указывает, что позиция текста [math]j[/math] фактически пропущена.

Остается показать, что число позиций несовпадений в таблице несовпадений образца достаточно для того, чтобы [math]merge[/math] нашла все, или, если их больше [math]k+1[/math], первые [math]k+1[/math] несовпадений для [math]y[i+1...j][/math]. Это можно показать следующим образом. Условие A выполняется не больше чем для [math]k+1[/math] позиции текста в диапазоне [math]y[i+1...j][/math]. Условие B выполняется для некоторого неизвестного числа позиций в этом же интервале. Строка [math]i-r[/math] в таблице несовпадений образца, [math]tm[i-r][1...2k+1][/math], содержит не больше чем [math]2k+1[/math] позиций несовпадений между двумя копиями образца, с соответствующим сдвигом [math]i-r[/math]. Если [math]pm[i-r][2k+1] \gt j - i[/math], то таблица содержит все позиции несовпадения образца самим с собой, у которых условие B выполняется для позиций текста в интервале [math]y[i+1...j][/math]. С другой стороны, если [math]pm[i-r][2k+1] \lt j-i[/math], то таблица может дать [math]2k+1[/math] позиций текста в диапазоне [math]y[i+1...j-1][/math], для которых выполняется условие B. Поскольку [math]j = r+tm[r][k+1][/math], в диапазоне [math]y[i+1...j-1][/math] имеется до [math]k[/math] позиций текста, для которых выполняется условие A. Таким образом, в худшем случае может быть [math]k[/math] позиций, для которых имеет место случай 3, и которые требуется сравнить напрямую. Остается по крайней мере [math]k+1[/math] позиций, удовлетворяющих условию B, но не условию A (случай 2), что является достаточным, чтобы заключить, что для данного положения образца относительно текста имеется не меньше [math]k+1[/math] несовпадений между текстом и образцом.

merge(i, r, j, b) u = 1 v = q while (b < k + 1) and (v < k + 2) and (i + pm[i - r][u] < j or tm[r][v] != m + 1) if i + pm[i - r][u] > r + tm[r][v] // Случай 2, условие A b++ tm[i][b] = tm[r][v] - (i - r) v++ else if i + pm[i - r][u] < r + tm[r, v] // Случай 2, условие B b++ tm[i][b] = pm[i - r][u] u++ else // Случай 3 I + PM[I - R, U] = R + TM[R, V] if x[ pm[i-r][u] ] != y[ i+pm[i-r][u] ] b++ tm[i][b] = pm[i - r][u] u++ v++

Построение pm

Теперь осталось только обратиться к вычислению таблицы несовпадений шаблона на стадии предварительных вычислений. Не теряя общности, можно предположить, что [math]m[/math] является некоторой степенью [math]2[/math]. В алгоритме предварительной обработки используется разбиение множества [math]{1, 2, ... , m-1}[/math] из [math]m-1[/math] строк [math]pm[/math] на следующие [math]\log m[/math] подмножеств:

[math]\{1\}, \{2, 3\}, \{4, 5, 6, 7\}, ... , \{m/2, ... , m-1\}[/math]

Алгоритм состоит из [math]\log m[/math] этапов. На этапе [math]s[/math], где [math]1 \leqslant s \lt \log m[/math], вычисляются строки [math]pm[/math] в множестве [math]s[/math], где множество [math]s[/math] – это [math]{2s-1, ... , 2s-1}[/math].

Метод, используемый для вычисления этой таблицы, основан на методе, используемом на стадии анализа текста. Рассмотрим алгоритм для этапа [math]s[/math]. На стадии [math]s[/math] входами для алгоритма анализа образца являются подстроки образца [math]x[1...m-2^{s-1}][/math] и [math]x[2^{s-1}+1...m][/math], которые трактуются здесь, соответственно, как образец и текст, и массив [math]pm[1...2^{s-1}-1][1...min\{2^{log(m)-s}4k+1, m-2^{s-1}\}][/math], содержащий выходы предыдущих [math]s - 1[/math] стадий. (Число элементов в строках подмассива будет объяснено позже). Выходы стадии [math]s[/math] вводятся в //todo. За исключением стадии [math]\log m[/math], на которой находят до [math]2k+1[/math] несовпадений, на стадии [math]s[/math] для каждой строки [math]pm[/math] требуется найти до [math]min\{2^{log(m)-s}2k+1, m-2^{s}\}[/math] несовпадений, а не до [math]k+1[/math], как в алгоритме анализа текста.

pm[[math]2^{h-1}[/math]...[math]2^{s-1}[/math]][1...min{[math]2^{\log (m-1)}2k-1[/math], [math]m-2^{s}[/math]}] = m+1 r = [math]2^{s-1}[/math] j = [math]2^{s-1}[/math] for i = [math]2^{s-1}[/math] to [math]2^{s} - 1[/math] b = 0 if i < j merge(I, R, J, B) if b < min{[math]2^{log(m-1)}2k-1, m-2^{s} [/math]} r = i extend(i, j, b)

Оценка работы

Теперь исследуем затраты времени на анализ текста. Если исключить вызовы процедур [math]merge[/math] и [math]extend[/math], каждая из [math]n-m+1[/math] итераций цикла анализа текста выполняется за фиксированное время, что дает в общей сложности время [math]O(n)[/math]. Общее число операций, выполняемых процедурой [math]extend[/math] во время вызовов равно [math]O(n)[/math], так как она проверяет каждый символ текста не больше одного раза. Процедура [math]merge[/math] при каждом вызове обрабатывает массив [math]pm[i-r][1...2k+1][/math] и [math]tm[r][1...k+1][/math], которые в сумме имеют [math]3k+2[/math] элементов. Время работы [math]merge[/math] можно рассчитать, соотнеся операции с фиксированным временем с каждым из этих входов, что дает время счета для каждого вызова, равное [math]O(k)[/math]. Таким образом, можно видеть, что общее время анализа текста составляет [math]O(nk)[/math].

Рассмотрим построение [math]pm[/math]Используя аргументы, аналогичные применявшимся при проверке корректности процедуры merge, можно показать, что для нахождения требуемого количества несовпадений на стадии s требуется [math]min\{2^{log(m)-s}4k+1, m-2^{s}\}[/math] позиций, для которых выполняется условие B, и в особом случае, а именно, на стадии [math]\log m[/math], требуется [math]4k + 1[/math] таких позиций.

На каждой стадии [math]s[/math] из [math]\log m[/math] стадий анализа образца цикл [math]for[/math] производит [math]2^{s-1}[/math] итераций [math](2^{s-1} \leqslant i \leqslant 2^{s}-1)[/math]. Если не считать время работы процедур [math]merge[/math] и [math]extend[/math], каждая итерация требует фиксированного времени. Для всех итераций на шаге [math]s[/math] процедуре [math]extend[/math] требуется время [math]O(m)[/math]. Ранее было показано, что время работы [math]merge[/math] пропорционально числу искомых несовпадений. Таким образом, каждый вызов [math]merge[/math] занимает время [math]O(min\{2^{log(m)-s}4k+1, m-2^{s}\})[/math], что равно [math]O(2k2^{\log (m-s)})[/math]. Таким образом, общее время для стадии [math]s[/math] равно [math]O(m+2^{l-1}(2k2^{\log (m-s)}))[/math] = [math]O(km)[/math]. Проведя суммирование по всем стадиям, получаем общее время счета [math]O(\sum_{i=1}^{\log m} km)[/math] = [math]O(km \log m)[/math]. Таким образом, общие затраты времени, включающие предварительную обработку образца и анализ текста, равны [math]O(k(n + m \log m))[/math].

Пример

Пусть [math]x = "tram"[/math], [math]y = "thetrippedtrap"[/math], [math]k = 2[/math].

tm	1	2	3	x[1..m]	y[i+1..i+m]
0	2	3	4	tram	thet
1	1	2	3	tram	hetr
2	1	2	3	tram	etri
3	3	4	5	tram	trip
4	1	2	3	tram	ripp
5	1	2	3	tram	ippe
6	1	2	3	tram	pped
7	1	2	3	tram	pedt
8	1	2	3	tram	edtr
9	1	2	3	tram	dtra
10	4	5	5	tram	trap

tm	1	2	3	4	5	x[1..m-i]	x[i+1..m]
1	1	2	3	5	5	tra	ram
2	1	2	5	5	5	tr	am
3	1	5	5	5	5	t	m