Двоичный каскадный сумматор — различия между версиями
Tanfilyev (обсуждение | вклад) |
м (ну блин) |
||
| Строка 7: | Строка 7: | ||
<Br/> | <Br/> | ||
Построим таблицу зависимости <tex>C_{i+1}</tex> от <tex>X_{i}, Y_{i}, C_{i}</tex>, и введем условные обозначения: | Построим таблицу зависимости <tex>C_{i+1}</tex> от <tex>X_{i}, Y_{i}, C_{i}</tex>, и введем условные обозначения: | ||
| − | < | + | {| border="1" |
| − | < | + | | x || y || <tex> C_i \rightarrow C_{i+1} </tex> || Условные обозначения ||align="center" | Действие |
| + | |- align="center" | ||
| + | | 0 || 0 || 0 || k(kill) || Поглощение переноса | ||
| + | |- align="center" | ||
| + | | 0 || 1 | ||
| + | | rowspan="2"| <tex> P_1 </tex> ||rowspan="2"| p(propagate) ||rowspan="2"| Перенос переноса | ||
| + | |- align="center" | ||
| + | | 1 || 0 | ||
| + | |- align="center" | ||
| + | | 1 || 1 || 1 || g(generate) || Порождение переноса | ||
| + | |} | ||
| + | |||
| + | |||
Обозначим композицию действий над переносами значком <tex>\bigotimes</tex> и рассмотрим таблицу: | Обозначим композицию действий над переносами значком <tex>\bigotimes</tex> и рассмотрим таблицу: | ||
{| border="1" | {| border="1" | ||
Версия 05:08, 16 января 2011
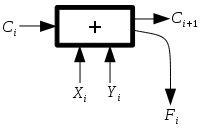
Рассмотрим один элемент полного сумматора:
Где - i-ный разряд суммируемых чисел, - Биты переноса, а - Результат сложения.
Построим таблицу зависимости от , и введем условные обозначения:
| x | y | Условные обозначения | Действие | |
| 0 | 0 | 0 | k(kill) | Поглощение переноса |
| 0 | 1 | p(propagate) | Перенос переноса | |
| 1 | 0 | |||
| 1 | 1 | 1 | g(generate) | Порождение переноса |
Обозначим композицию действий над переносами значком и рассмотрим таблицу:
| k | p | g | |
|---|---|---|---|
| k | k | k | g |
| p | k | p | g |
| g | k | g | g |
Пример:
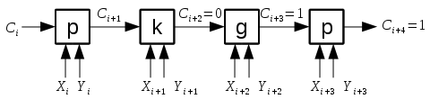
Таким образом функцию можно определить как последнее не "P".
Пусть , тогда: .
Пусть элемент
![]() возвращает двух функций,
возвращает двух функций,
а элемент
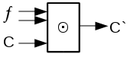 возвращает , старший бит сумматора.
возвращает , старший бит сумматора.
Схема двоичного каскадного сумматора выглядит следующим образом:
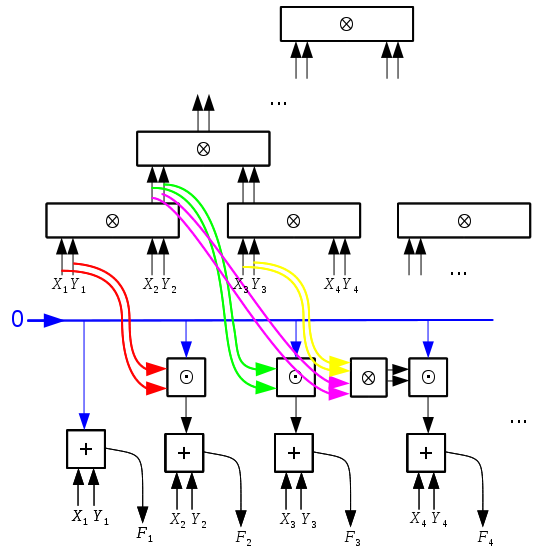
Сумматор состоит из двух частей. Первой частью является дерево отрезков [1], с помощью которого, вычисляется бит переноса. Вторая часть это группа полных сумматоров, вычисляющих ответ.