Предиктивный синтаксический анализ — различия между версиями
(→Пример) |
|||
| Строка 14: | Строка 14: | ||
addChild(Node) // функция, подвешивающая поддерево к данному узлу | addChild(Node) // функция, подвешивающая поддерево к данному узлу | ||
| − | + | ||
| + | [[Файл:string_token.png|300px|thumb|right|Рисунок 1.]] | ||
| + | |||
Токен {{---}} один или несколько нетерминалов, для удобства объединяемые по смыслу в одну логическую единицу. | Токен {{---}} один или несколько нетерминалов, для удобства объединяемые по смыслу в одну логическую единицу. | ||
| + | |||
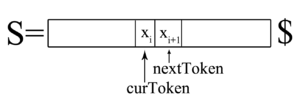
curToken {{---}} текущий токен строки. | curToken {{---}} текущий токен строки. | ||
| + | |||
nextToken() {{---}} записывает в curToken следующий за ним токен. | nextToken() {{---}} записывает в curToken следующий за ним токен. | ||
| + | |||
A() : Node | A() : Node | ||
| Строка 135: | Строка 140: | ||
Функции для <tex>T</tex> и <tex>T'</tex> строятся аналогично. | Функции для <tex>T</tex> и <tex>T'</tex> строятся аналогично. | ||
| − | |||
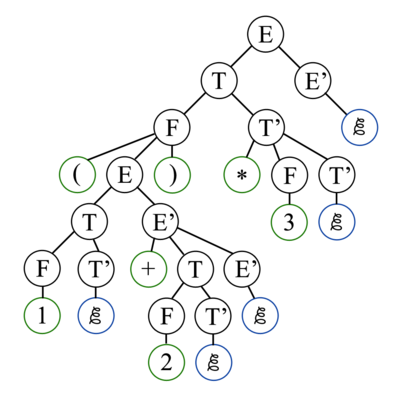
| − | [[Файл:parse_ex1.png|400px|thumb|right|Рисунок | + | [[Файл:parse_ex1.png|400px|thumb|right|Рисунок 2. Дерево разбора выражения (1 + 2) * 3]] |
| + | |||
| + | Рассмотрим дерево разбора для выражения (1 + 2) * 3 и несколько первых шагов алгоритма рекурсивного разбора. Сначала вызывается функция стартового нетерминала грамматики, то есть <tex>Е</tex>. Так как первым токеном является '(', то будет использовано первое правило разбора <tex>TE'</tex>. Поэтому к вершине с меткой <tex>Е</tex> добавятся два ребёнка: <tex>T</tex> и <tex>E'</tex>. А рекурсивный разборщик перейдёт к нетерминалу <tex>T</tex>По-прежнему curToken равен '(', поэтому в <tex>F</tex> сработает второй case, первым ребёнком добавится '(', curToken станет равен <tex>1</tex>, а разборщик перейдёт к нетерминалу <tex>E</tex>. После того как выражение после '(', которое выводится из <tex>E</tex>, будет полностью разобрано, функция рекурсивного разбора для <tex>F</tex> добавит ')' последним сыном к этому нетерминалу. | ||
| + | |||
| + | Продолжая в том же духе, мы построим всё дерево разбора данного выражения. | ||
{{TODO | t = Построение таблицы предиктивного анализа}} | {{TODO | t = Построение таблицы предиктивного анализа}} | ||
Версия 20:07, 24 мая 2015
Для LL(1)-грамматик возможна автоматическая генерация парсеров, если известны множества FIRST и FOLLOW. Существуют общедоступные генераторы: ANTLR, GNU bison, Yacc.
Общая схема построения парсеров с помощью и
Пусть — LL(1)-грамматика. Построим для нее парсер.
Для каждого нетерминала : создадим функцию A() : Node, возвращающую фрагмент дерева разбора, выведенный из нетерминала .
Здесь Node — структура вида:
Node
children : list<Node>
value : string // имя нетерминала или текст терминала
addChild(Node) // функция, подвешивающая поддерево к данному узлу
Токен — один или несколько нетерминалов, для удобства объединяемые по смыслу в одну логическую единицу.
curToken — текущий токен строки.
nextToken() — записывает в curToken следующий за ним токен.
A() : Node
res = Node("A")
switch (curToken) :
case :
//
for
if is terminal
consume()
res.addChild(new Node("")
nextToken()
else
Node t =
res.addChild(t)
break
case :
...
break
...
default :
error("unexpected char")
return res
consume(char c)
if (curToken != c)
error("expected" + c)
nextToken()
Такой парсер не только разбирает строку, но и находит ошибки в неудовлетворяющих грамматике выражениях.
Пример
Рассмотрим построение парсера на примере LL(1)-грамматики арифметических выражений.
Построим для нее множества FIRST и FOLLOW (их построение подробно разобрано здесь).
| Правило | FIRST | FOLLOW |
|---|---|---|
Построим функции обработки некоторых нетерминалов.
E()
res = Node("E")
switch(curToken)
case 'n', '(' :
res.addChild(T())
res.addChild(E'())
break
default :
error("unexpected char")
return res
E'()
res = Node("E'")
switch(curToken)
case '+' :
consume('+')
res.addChild(Node("+"))
res.addChild(T())
res.addChild(E'())
break
case '$', ')' :
break
default :
error("unexpected char")
return res
F()
res = Node("F")
switch(curToken)
case 'n' :
consume('n')
res.addChild(Node("n"))
break
case '(' :
consume('(')
res.addChild(Node("("))
res.addChild(E())
consume(')')
res.addChild(Node(")"))
default :
error("unexpected char")
return res
Функции для и строятся аналогично.
Рассмотрим дерево разбора для выражения (1 + 2) * 3 и несколько первых шагов алгоритма рекурсивного разбора. Сначала вызывается функция стартового нетерминала грамматики, то есть . Так как первым токеном является '(', то будет использовано первое правило разбора . Поэтому к вершине с меткой добавятся два ребёнка: и . А рекурсивный разборщик перейдёт к нетерминалу По-прежнему curToken равен '(', поэтому в сработает второй case, первым ребёнком добавится '(', curToken станет равен , а разборщик перейдёт к нетерминалу . После того как выражение после '(', которое выводится из , будет полностью разобрано, функция рекурсивного разбора для добавит ')' последним сыном к этому нетерминалу.
Продолжая в том же духе, мы построим всё дерево разбора данного выражения.
TODO: Построение таблицы предиктивного анализа