Суффиксный массив

Определение:

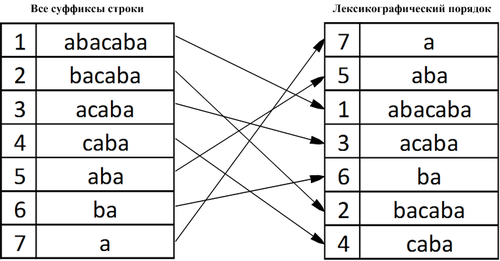
Cуффиксным массивом (англ. suffix array) строки [math]s[1 .. n][/math] называется массив [math]suf[/math] целых чисел от [math]1[/math] до [math]n[/math], такой, что суффикс [math]s[suf[i]..n][/math] — [math]i[/math]-й в лексикографическом порядке среди всех непустых суффиксов строки [math]s[/math].

Пример

[math]s = abacaba[/math]

Значит, суффиксный массив для строки [math]s[/math] равен [math][7, 5, 1, 3, 6, 2, 4][/math].

Применения

• Позволяет найти все вхождения образца [math]p[/math] в строку [math]s[/math] за время [math]O(|p| + \log(|s|))[/math].
• Позволяет вычислить наибольший общий префикс (англ. longest common prefix, LCP) для всех соседних в лексикографическом порядке суффиксов строки [math]s[/math] за [math]O(|s|)[/math], то есть построить массив [math]LCP[1 .. |s| - 1][/math], где [math]LCP[i][/math] — длина наибольшего общего префикса суффиксов [math]s[suf[i] .. |s|][/math] и [math]s[suf[i + 1] .. |s|][/math].
• Позволяет найти количество различных подстрок в строке за время [math]O(|s| \log(|s|))[/math] и [math]O(|s|)[/math] дополнительной памяти.
• Позволяет найти наименьший циклический сдвиг строки за время [math]O(|s| \log(|s|))[/math].
• Позволяет найти максимальную по длине строку, ветвящуюся влево и вправо за время [math]SA + O(n)[/math], где [math]SA[/math] — время построения суффиксного массива.

Поиск строки максимальной длины, ветвящейся влево и вправо

Определение:

Строка [math]s[/math] называется ветвящейся вправо в [math]t[/math] (англ. right branching string), если существуют символы [math]c[/math] и [math]d[/math], такие что [math]c[/math] [math]\ne[/math] [math]d[/math] : [math]sc[/math] и [math]sd[/math] — подстроки [math]t[/math]. Аналогично, ветвящаяся влево (англ. left branching), если [math]cs[/math] и [math]ds[/math] — подстроки [math]t[/math].

Определение:

Левый символ для позиции [math]i[/math] строки [math]S[/math] — это символ [math]S(i-1)[/math].

Что бы найти максимальную строку, ветвящуюся влево и вправо, строится суффиксный массив из которого исключается суффикс равный самой строке, к примеру для строки [math]aabcabd[/math] :

Суффиксный массив
[math]abcabd[/math]
[math]abd[/math]
[math]bcabd[/math]
[math]bd[/math]
[math]cabd[/math]
[math]d[/math]

Далее вычисляется [math]LCP[/math] для суффиксного массива, и находятся левые символы суффиксов:

Левый символ	Суффиксный массив	LCP
[math]a[/math]	[math]abcabd[/math]	[math]\#[/math]
[math]c[/math]	[math]abd[/math]	[math]2[/math]
[math]a[/math]	[math]bcabd[/math]	[math]0[/math]
[math]a[/math]	[math]bd[/math]	[math]1[/math]
[math]b[/math]	[math]cabd[/math]	[math]0[/math]
[math]b[/math]	[math]d[/math]	[math]0[/math]

Максимальная строка, ветвящаяся влево и вправо, находится путём проверки значений [math]LCP[/math] и левого символа: Ветвление вправо:

• Если [math]LCP[/math] от пары суффиксов [math]s_1[/math] и [math]s_2[/math] больше нуля и не равен длинам этих суффиксов, то строка [math]s[/math], равная [math]s_1[1..LCP(s_1,s_2)][/math], ветвится вправо.

Ветвление влево:

• Если левые символы [math]s_1[/math] и [math]s_2[/math] не равны, то строка [math]s[/math], равная [math]s_1[1..LCP(s_1,s_2)][/math], ветвится влево.

Если выполнены оба условия, то строка ветвится вправо и влево. С помощью этой проверки находится максимальная строка, ветвящаяся влево и вправо, за [math]O(n)[/math].

См. также

• Построение суффиксного массива с помощью стандартных методов сортировки
• Алгоритм поиска подстроки в строке с помощью суффиксного массива
• Алгоритм Касаи и др.

Источники

• Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.
• MAXimal :: algo :: Суффиксный массив
• Википедия — Суффиксный массив
• Wikipedia — Suffix array
• Habrahabr — Суффиксный массив — удобная замена суффиксного дерева