Список с пропусками — различия между версиями
(Отмена правки 47987 участника 188.227.78.59 (обсуждение)) |
|||
| Строка 1: | Строка 1: | ||
| − | '''Список с пропусками''' (''skip list'') | + | '''Список с пропусками''' (''skip-list'') — вероятностная структура данных, основанная на нескольких отсортированных односвязных списках. |
| − | + | Отсортированный связный список является простейшей структурой с временем поиска <tex>\Theta(n)</tex>. Добавление дополнительных уровней, обеспечивающих быстрый доступ через несколько элементов, поможет улучшить асимптотику до <tex>\Theta(\log(n))</tex>. | |
| − | + | ==Описание== | |
| − | |||
| − | == | ||
Список с пропусками строится на основе существующего односвязного отсортированного списка. | Список с пропусками строится на основе существующего односвязного отсортированного списка. | ||
[[Файл:SimpleList.png]] | [[Файл:SimpleList.png]] | ||
| − | Добавив дополнительные уровни, каждый из которых представляет предыдущий уровень без нечетных элементов, мы получим возможность осуществлять поиск, вставку и удаление элементов подобно операциям с двоичным деревом поиска. Соответственно, асимптотика этих операций будет составлять <tex>\Theta(\log(n))</tex>. | + | Добавив дополнительные уровни, каждый из которых представляет предыдущий уровень без нечетных элементов, мы получим возможность осуществлять поиск, вставку и удаление элементов подобно операциям с двоичным деревом поиска. Одинаковые элементы связаны между уровнями. Соответственно, асимптотика этих операций будет составлять <tex>\Theta(\log(n))</tex>. |
[[Файл:SkipList.png]] | [[Файл:SkipList.png]] | ||
| Строка 16: | Строка 14: | ||
==Операции над структурой== | ==Операции над структурой== | ||
===Поиск элемента=== | ===Поиск элемента=== | ||
| − | Допустим, что в нашем списке с пропусками существуют <tex> | + | Допустим, что в нашем списке с пропусками существуют два уровня: <tex>L_1</tex>, в котором содержатся все элементы и <tex>L_2</tex>, в котором присутствует только часть из них. Между одинаковыми элементами этих двух списков существуют ссылки. |
В таком случае алгоритм поиска в этой структуре будет представлять из себя следующие операции: | В таком случае алгоритм поиска в этой структуре будет представлять из себя следующие операции: | ||
| − | # Начинаем поиск элемента в верхнем | + | # Начинаем поиск элемента в верхнем левом углу |
| − | + | # Передвигаться будем по списку <tex>L_2</tex>, пока значение в следующей ячейке меньше или равно ключу | |
| − | # Переместиться | + | # Переместиться в нижний уровень и продолжить аналогичный метод поиска по списку <tex>L_1</tex> |
Пример поиска числа 8 в списке из описания: | Пример поиска числа 8 в списке из описания: | ||
| Строка 27: | Строка 25: | ||
[[Файл:SkipListSearch.png]] | [[Файл:SkipListSearch.png]] | ||
| − | |||
Тогда время работы алгоритма поиска будет зависеть от количества элементов на уровне <tex>L_2</tex>. Представим, что на этот уровень у нас случайным образом попало несколько элементов. Следовательно в худшем случае поиска мы получим следующую оценку на время работы: | Тогда время работы алгоритма поиска будет зависеть от количества элементов на уровне <tex>L_2</tex>. Представим, что на этот уровень у нас случайным образом попало несколько элементов. Следовательно в худшем случае поиска мы получим следующую оценку на время работы: | ||
| Строка 38: | Строка 35: | ||
<tex> \sqrt{n} + \dfrac{n}{\sqrt{n}} = 2 \sqrt{n}</tex> | <tex> \sqrt{n} + \dfrac{n}{\sqrt{n}} = 2 \sqrt{n}</tex> | ||
| − | + | Делая аналогичные подсчеты для списков с пропусками, в которых содержится больше уровней, получаем: | |
| − | Для <tex>\ | + | * Для трех уровней: <tex> 3 \sqrt[3]{n}</tex> |
| − | + | * Для четырех уровней: <tex> 4 \sqrt[4]{n}</tex> | |
| − | + | * Для пяти уровней: <tex> 5 \sqrt[5]{n}</tex> | |
| − | < | + | * Для <tex>\log{n}</tex> уровней: <tex> \log{n} \times \sqrt[\log{n}]{n} = n ^ {\frac{1}{log{n}}} \log{n} = n ^ {\log_n{2}} \log{n} = 2\log{n}</tex> |
| − | + | ||
| − | + | В списках с пропусками, в которых содержится <tex>\log{n}</tex> уровней будет себя вести очень похоже на сбалансированные бинарные деревья поиска. В идеальной данной структуре соотношение между соседними уровнями будет равняться двум. Поиск в <tex>\log{n}</tex> списке с пропусками будет осуществляться за асимптотическое время <tex>O(\log{n})</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Вставка элемента=== | ===Вставка элемента=== | ||
Для вставки элемента в список с пропусками, нам необходимо выполнить следующие шаги: | Для вставки элемента в список с пропусками, нам необходимо выполнить следующие шаги: | ||
| Строка 66: | Строка 52: | ||
Таким образом, если использовать честную монету, то математическое ожидание количества элементов на втором уровне равняется <tex>\dfrac{n}{2}</tex>, на третьем уровне <tex>\dfrac{n}{4}</tex> и т.д. На уровне <tex>\log{n}</tex> у нас окажется один элемент. Ну и соответственно вероятности попасть элементу на второй уровень — это <tex>\dfrac{1}{2}</tex>, на третий <tex>\dfrac{1}{4}</tex> и т.д. Вероятность попасть на уровень <tex>\log{n}</tex> равна <tex>\dfrac{1}{n}</tex>. | Таким образом, если использовать честную монету, то математическое ожидание количества элементов на втором уровне равняется <tex>\dfrac{n}{2}</tex>, на третьем уровне <tex>\dfrac{n}{4}</tex> и т.д. На уровне <tex>\log{n}</tex> у нас окажется один элемент. Ну и соответственно вероятности попасть элементу на второй уровень — это <tex>\dfrac{1}{2}</tex>, на третий <tex>\dfrac{1}{4}</tex> и т.д. Вероятность попасть на уровень <tex>\log{n}</tex> равна <tex>\dfrac{1}{n}</tex>. | ||
| − | Используя монетку с распределением отличным от {<tex>\dfrac{1}{2}</tex>, <tex>\dfrac{1}{2}</tex>}, можно влиять на количество элементов на верхних уровнях. | + | Используя монетку с распределением отличным от {<tex>\dfrac{1}{2}</tex>, <tex>\dfrac{1}{2}</tex>}, можно влиять на количество элементов на верхних уровнях (и соответственно, на количество уровней). Однако как при большем количестве проталкиваний элементов на уровень выше, так и при меньшем, количество шагов при поиске элемента возрастает. При распределении {0, 1} структура превращается в обыкновенный список, при {1, 0} {{---}} в <tex>n</tex> параллельных списков. В обоих случаях |
| − | |||
| − | |||
| − | |||
===Удаление элемента=== | ===Удаление элемента=== | ||
| Строка 77: | Строка 60: | ||
==Псевдокод== | ==Псевдокод== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<code> | <code> | ||
| − | + | const float P = 0.5 | |
| − | + | ||
| − | while | + | int random_level() |
| − | + | int lvl = (int)(log(frand())/log(1.-P)) | |
| − | + | if lvl < MAX_LEVEL | |
| + | return lvl | ||
| + | return MAX_LEVEL | ||
| + | |||
| + | boolean Find (int key) | ||
| + | SkipNode x = header | ||
| + | for i = level to 0 | ||
| + | while x.forward[i] != NULL and x.forward[i].value < key | ||
| + | x = x.forward[i] | ||
| + | x = x.forward[0] | ||
| + | return x != NULL && x.value == key | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | void Insert(int value) | ||
| + | SkipNode x = header | ||
| + | SkipNode update | ||
| + | update.assign(MAX_LEVEL + 1, 0) | ||
| + | |||
| + | for i = level to 0 | ||
| + | while x.forward[i] != NULL and x.forward[i].value < value | ||
| + | x = x.forward[i] | ||
| + | update[i] = x | ||
| + | x = x.forward[0] | ||
| + | if x == NULL or x.value != value | ||
| + | int lvl = random_level() | ||
| + | if lvl > level | ||
| + | for i = level + 1 to lvl | ||
| + | update[i] = header | ||
| + | level = lvl | ||
| + | x = new SkipNode(lvl, value) | ||
| + | for i = 0 to lvl | ||
| + | x.forward[i] = update[i].forward[i] | ||
| + | update[i].forward[i] = x | ||
| + | |||
| + | |||
| + | void Erase(int value) | ||
| + | SkipNode x = header | ||
| + | SkipNode update | ||
| + | update.assign(MAX_LEVEL + 1, 0) | ||
| + | for i = level to 0 | ||
| + | while x.forward[i] != NULL and x.forward[i].value < value | ||
| + | x = x.forward[i] | ||
| + | update[i] = x | ||
| + | x = x.forward[0] | ||
| + | if x.value == value | ||
| + | for i = 0 to level | ||
| + | if update[i].forward[i] != x | ||
| + | break | ||
| + | update[i].forward[i] = x.forward[i]; | ||
| + | delete x | ||
| + | while level > 0 or header.forward[level] == NULL | ||
| + | level-- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</code> | </code> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Ссылки== | ==Ссылки== | ||
*[http://habrahabr.ru/post/111913/ Хабрахабр — Списки с пропусками] | *[http://habrahabr.ru/post/111913/ Хабрахабр — Списки с пропусками] | ||
Версия 18:40, 7 июня 2015
Список с пропусками (skip-list) — вероятностная структура данных, основанная на нескольких отсортированных односвязных списках.
Отсортированный связный список является простейшей структурой с временем поиска . Добавление дополнительных уровней, обеспечивающих быстрый доступ через несколько элементов, поможет улучшить асимптотику до .
Содержание
Описание
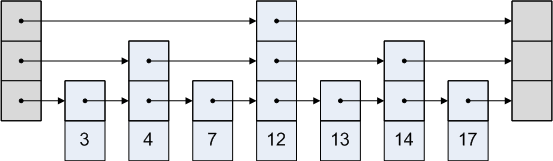
Список с пропусками строится на основе существующего односвязного отсортированного списка.
Добавив дополнительные уровни, каждый из которых представляет предыдущий уровень без нечетных элементов, мы получим возможность осуществлять поиск, вставку и удаление элементов подобно операциям с двоичным деревом поиска. Одинаковые элементы связаны между уровнями. Соответственно, асимптотика этих операций будет составлять .
Операции над структурой
Поиск элемента
Допустим, что в нашем списке с пропусками существуют два уровня: , в котором содержатся все элементы и , в котором присутствует только часть из них. Между одинаковыми элементами этих двух списков существуют ссылки.
В таком случае алгоритм поиска в этой структуре будет представлять из себя следующие операции:
- Начинаем поиск элемента в верхнем левом углу
- Передвигаться будем по списку , пока значение в следующей ячейке меньше или равно ключу
- Переместиться в нижний уровень и продолжить аналогичный метод поиска по списку
Пример поиска числа 8 в списке из описания:
Тогда время работы алгоритма поиска будет зависеть от количества элементов на уровне . Представим, что на этот уровень у нас случайным образом попало несколько элементов. Следовательно в худшем случае поиска мы получим следующую оценку на время работы:
Минимизируя, мы получаем, что
В итоге время за которое мы найдем элемент в списке с пропусками с двумя уровнями будет равняться:
Делая аналогичные подсчеты для списков с пропусками, в которых содержится больше уровней, получаем:
- Для трех уровней:
- Для четырех уровней:
- Для пяти уровней:
- Для уровней:
В списках с пропусками, в которых содержится уровней будет себя вести очень похоже на сбалансированные бинарные деревья поиска. В идеальной данной структуре соотношение между соседними уровнями будет равняться двум. Поиск в списке с пропусками будет осуществляться за асимптотическое время .
Вставка элемента
Для вставки элемента в список с пропусками, нам необходимо выполнить следующие шаги:
- Найти с помощью алгоритма поиска позицию, куда нам надо вставить этот элемент
- Вставить наш элемент в нижний уровень списка с пропусками
- «Подбросить монетку» и в зависимости от результата протолкнуть элемент на уровень выше
- Повторять предыдущий шаг до тех пор, пока у нас «подброс монетки» дает положительный результат
Таким образом, если использовать честную монету, то математическое ожидание количества элементов на втором уровне равняется , на третьем уровне и т.д. На уровне у нас окажется один элемент. Ну и соответственно вероятности попасть элементу на второй уровень — это , на третий и т.д. Вероятность попасть на уровень равна .
Используя монетку с распределением отличным от {, }, можно влиять на количество элементов на верхних уровнях (и соответственно, на количество уровней). Однако как при большем количестве проталкиваний элементов на уровень выше, так и при меньшем, количество шагов при поиске элемента возрастает. При распределении {0, 1} структура превращается в обыкновенный список, при {1, 0} — в параллельных списков. В обоих случаях
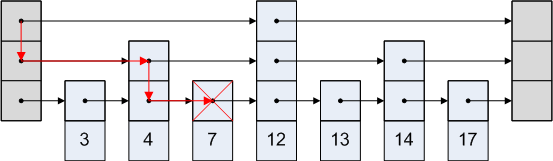
Удаление элемента
Алгоритм удаления достаточно тривиален.
- Найти удаляемый элемент
- Удалить его со всех уровней
Псевдокод
const float P = 0.5
int random_level()
int lvl = (int)(log(frand())/log(1.-P))
if lvl < MAX_LEVEL
return lvl
return MAX_LEVEL
boolean Find (int key)
SkipNode x = header
for i = level to 0
while x.forward[i] != NULL and x.forward[i].value < key
x = x.forward[i]
x = x.forward[0]
return x != NULL && x.value == key
void Insert(int value)
SkipNode x = header
SkipNode update
update.assign(MAX_LEVEL + 1, 0)
for i = level to 0
while x.forward[i] != NULL and x.forward[i].value < value
x = x.forward[i]
update[i] = x
x = x.forward[0]
if x == NULL or x.value != value
int lvl = random_level()
if lvl > level
for i = level + 1 to lvl
update[i] = header
level = lvl
x = new SkipNode(lvl, value)
for i = 0 to lvl
x.forward[i] = update[i].forward[i]
update[i].forward[i] = x
void Erase(int value)
SkipNode x = header
SkipNode update
update.assign(MAX_LEVEL + 1, 0)
for i = level to 0
while x.forward[i] != NULL and x.forward[i].value < value
x = x.forward[i]
update[i] = x
x = x.forward[0]
if x.value == value
for i = 0 to level
if update[i].forward[i] != x
break
update[i].forward[i] = x.forward[i];
delete x
while level > 0 or header.forward[level] == NULL
level--