LR(0)-разбор

LR(0)-разборщик это частный случай LR(k)-разборщикa. Заметим, что в данном случае [math]k=0[/math], то есть решение о своих действиях принимается только на основании содержимого стека, не учитывая символы входной цепочки.

Построение автомата и управляющей таблицы

В статье про LR(k)-разборщик, управляющая программа одинакова для всех LR-анализаторов, а таблица и автомат изменяются от одного анализатора к другому.

Автомат

Каждое состояние автомата будет состоять из LR(0)-ситуации.

Определение:

Пусть [math]\Gamma =\langle \Sigma, N, S, P \rangle[/math] — КС-грамматика и [math]A \to w_1 w_2 \in P[/math]. Композицию [math][A \to w_1 \cdot w_2] [/math] назовем LR(0)-ситуацией (англ. LR(0)-item)

В начале работы стек пуст, и указатель входной цепочки находится перед ее первым символом. Этому состоянию соответствует ситуация [math][E_0 \to \cdot E][/math], где [math]E_0[/math] — нетерминал, добавленный при пополнении грамматики, [math]E[/math] — стартовый нетерминал. Назовем это состояние [math]0[/math]. Входная цепочка может начинаться с любого терминального символа, с которого начинается правая часть любого правила с левой частью [math]E[/math]. Построим соответствующий переход по следующей схеме:

[math]{[} A \to \alpha \cdot B \beta] \xrightarrow{\varepsilon} {[} B \to \cdot \gamma] [/math]

Теперь мы должны выяснить, что произойдет, если анализатор выполнит перенос. Предположим, что мы выполним перенос [math]c[/math] или перенос [math]B[/math]:

[math]{[} A \to \alpha \cdot c \beta] \xrightarrow{\text{c}} {[} A \to \alpha c \cdot \beta] [/math]

[math]{[} A \to \alpha \cdot B \beta] \xrightarrow{\text{B}} {[} A \to \alpha B \cdot \beta] [/math]

Таким образом, мы определяем новые состояния, в которое автомат перейдет после переноса того или иного терминала или нетерминала.

Надо заметить, что алгоритм LR-разбора похож на алгоритм Эрли.

Базовые операции

Заметим, что хранить в каждом состоянии только по одной ситуации не имеет смысла, поэтому пусть в каждое стостояние будет представлять множество ситуаций, а переходы — термилалы и нетермилалы. Для этого определим базовые операции [math]closure (I)[/math] и [math]goto (I, X)[/math], где [math]I[/math] — множество ситуаций, [math]X[/math] — символ грамматики (терминал или нетерминал).

• Операция [math]closure[/math] добавляет ситуации к множеству ситуаций, у которых точка стоит слева от нетерминала. Добавляются те ситуации, которые получаются из правил, в левой части которого находится этот нетерминал.

• Операция [math]goto[/math] "переносит" точку после символа [math]X[/math]. Это означает переход из одного состояния в другое под воздействием символа [math]X[/math].

Построение автомата

Теперь обсудим алгоритм построения конечного автомата. Обозначим [math]T[/math] множество состояний, [math]E[/math] — множество переходов.

1. Изначальное состояние содержит одно правило: [math]E_0 \to E[/math],
2. Для текущего состояния делаем операцию [math]closure[/math],
3. По всем возможный символам для каждой ситуации добавляем переходы, используя операцию [math]goto[/math],
4. Если множество [math]T[/math] или [math]E[/math] во втором или третьем пункте изменилось, возвращаемся ко второму шагу.

Управляющая таблица

После того, как автомат построен, можно построить управляющую таблицу.

Обращение к таблице происходит следующим образом [math]\mathtt{T[state, token]}[/math], где

• [math]\mathtt{state}[/math] — состояние автомата,
• [math]\mathtt{token}[/math] — входной символ;

В соответствии со структурой управляющей таблицы будем действовать следующим образом:

1. Для каждого ребра [math]I \xrightarrow{\text{X}} J [/math] (из состояния [math]I[/math] в состояние [math]J[/math] по [math]X[/math]) мы поместим в позицию [math]T[I,X][/math]
   • [math]s(J)[/math] (сокр. от shift) , если [math]X[/math] — терминал,
   • [math]J[/math], если [math]X[/math] — нетерминал.
2. Для состояния [math]I[/math], содержащего ситуацию [math][A\to w \cdot][/math] в позицию [math]T[I, Y][/math] для каждого терминала [math]Y[/math]
   • Поместим [math]r(n)[/math] (сокр. от reduce), где [math]n[/math] — это номер правила в изначальной грамматике.
   • Запись [math]r(0)[/math] означает допуск.
3. Пустая ячейка означает ошибочную ситуацию.

Пример

Для иллюстрации алгоритма LR(0)-разборщика мы будем использовать грамматику:

[math] E \to E + T \\ E \to T \\ T \to {\bf n} \\ T \to (E) \\ [/math]

Обратим внимание, что данная грамматика является леворекурсивной, поэтому нисходящий разборщик не сможет осуществить разбор слова из этой грамматики.

Пополнение грамматики

Для начала переходим к Пополненной грамматике:

[math] E_0 \to E \\ E \to E + T \\ E \to T \\ T \to {\bf n} \\ T \to (E) \\ [/math]

Построение автомата

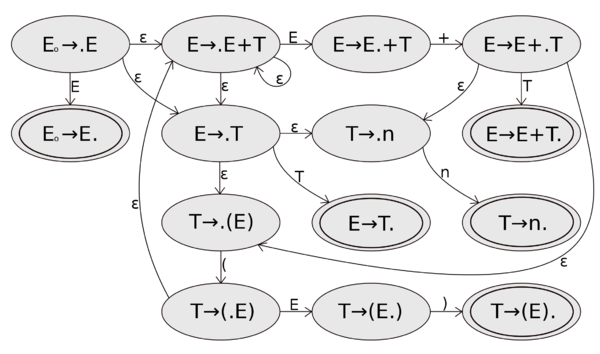
[math]0[/math] состоянию будет соответствует ситуация [math][E_0 \to \cdot E][/math]. Добавляем остальные состояния и получаем следующий НКА:

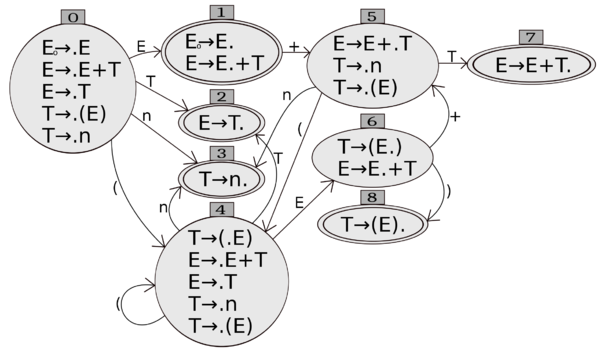
Теперь в одно состояние перемещаем все ситуации, в которые идут [math]\varepsilon[/math]-переходы. Получаем ДКА:

Заполнение управляющей таблицы

Пронумеруем правила для выполнения свертки:

[math] (0)\ E_0 \to E\\ (1)\ E \to E + T\\ (2)\ E \to T\\ (3)\ T \to {\bf n} \\ (4)\ T \to (E) \\ [/math]

Управляющая таблица будет выглядеть так:

	[math]E[/math]	[math]T[/math]	[math]n[/math]	[math]+[/math]	[math]([/math]	[math])[/math]	[math]\$[/math]
[math]0[/math]	[math]1[/math]	[math]2[/math]	[math]s(3)[/math]		[math]s(4)[/math]
[math]1[/math]				[math]s(5)[/math]			[math]r(0)[/math]
[math]2[/math]				[math]r(2)[/math]		[math]r(2)[/math]	[math]r(2)[/math]
[math]3[/math]				[math]r(3)[/math]		[math]r(3)[/math]	[math]r(3)[/math]
[math]4[/math]	[math]6[/math]	[math]2[/math]	[math]s(3)[/math]		[math]s(4)[/math]
[math]5[/math]		[math]7[/math]	[math]s(3)[/math]		[math]s(4)[/math]
[math]6[/math]				[math]s(5)[/math]		[math]s(8)[/math]
[math]7[/math]				[math]r(1)[/math]		[math]r(1)[/math]	[math]r(1)[/math]
[math]8[/math]				[math]r(4)[/math]		[math]r(4)[/math]	[math]r(4)[/math]

LR(0)-разбора конкретной строки

Пример будет для строки [math](n_1+n_2)+n_3[/math]

Строка	Стек	[math]curState[/math]	[math]curToken[/math]	[math]T[curState,curToken][/math]	Комментарий
[math](n_1+n_2)+n_3\$[/math]	[math]0[/math]	[math]0[/math]	[math]([/math]	[math]shift\ 4[/math]	Перенос [math]"("[/math]. Переход в [math]4[/math] состояние.
[math]n_1+n_2)+n_3\$[/math]	[math]0\ (4[/math]	[math]4[/math]	[math]n_1[/math]	[math]shift\ 3[/math]	Перенос [math]"n_1"[/math]. Переход в [math]3[/math] состояние.
[math]+n_2)+n_3\$[/math]	[math]0\ (4\ n_{1}3[/math]	[math]3[/math]	[math]+[/math]	[math]reduce\ 3[/math]	Свертка: [math]T \to \bf n[/math]. Удаление из стека [math]n_{1}3[/math]. Переход в [math]4[/math] состояние. Добавление в стек [math]T2[/math]. Переход в [math]2[/math] состояние.
[math]+n_2)+n_3\$[/math]	[math]0\ (4\ T2[/math]	[math]2[/math]	[math]+[/math]	[math]reduce\ 2[/math]	Свертка: [math]E \to T[/math]. Удаление из стека [math]T2[/math]. Переход в [math]4[/math] состояние. Добавление в стек [math]E6[/math]. Переход в [math]6[/math] состояние.
[math]+n_2)+n_3\$[/math]	[math]0\ (4\ E6[/math]	[math]6[/math]	[math]+[/math]	[math]shift\ 5[/math]	Перенос [math]"+"[/math]. Переход в [math]5[/math] состояние.
[math]n_2)+n_3\$[/math]	[math]0\ (4\ E6\ +5[/math]	[math]5[/math]	[math]n_2[/math]	[math]shift\ 3[/math]	Перенос [math]"n_2"[/math]. Переход в [math]3[/math] состояние.
[math])+n_3\$[/math]	[math]0\ (4\ E6\ +5\ n_23[/math]	[math]3[/math]	[math])[/math]	[math]reduce\ 3 [/math]	Свертка: [math]T \to \bf n[/math]. Удаление из стека [math]n_{2}3[/math]. Переход в [math]5[/math] состояние. Добавление в стек [math]T7[/math]. Переход в [math]7[/math] состояние.
[math])+n_3\$[/math]	[math]0\ (4\ E6\ +5\ T7[/math]	[math]7[/math]	[math])[/math]	[math]reduce\ 1 [/math]	Свертка: [math]E \to E + T[/math]. Удаление из стека [math]E6\ +5\ T7[/math]. Переход в [math]4[/math] состояние. Добавление в стек [math]E6[/math]. Переход в [math]6[/math] состояние.
[math])+n_3\$[/math]	[math]0\ (4\ E6[/math]	[math]6 [/math]	[math])[/math]	[math]shift\ 8[/math]	Перенос [math]")"[/math]. Переход в [math]8[/math] состояние.
[math]+n_3\$[/math]	[math]0\ (4\ E6\ )8[/math]	[math]8 [/math]	[math]+[/math]	[math]reduce\ 4[/math]	Свертка: [math]T \to (E)[/math]. Удаление из стека [math](4\ E6\ )8[/math]. Переход в [math]0[/math] состояние. Добавление в стек [math]T2[/math]. Переход в [math]2[/math] состояние.
[math]+n_3\$[/math]	[math]0\ T2[/math]	[math]2[/math]	[math]+[/math]	[math]reduce\ 2[/math]	Свертка: [math]E \to T[/math]. Удаление из стека [math]T2[/math]. Переход в [math]0[/math] состояние. Добавление в стек [math]E1[/math]. Переход в [math]1[/math] состояние.
[math]+n_3\$[/math]	[math]0\ E1[/math]	[math]1[/math]	[math]+[/math]	[math]shift\ 5[/math]	Перенос [math]"+"[/math]. Переход в [math]5[/math] состояние.
[math]n_3\$[/math]	[math]0\ E1\ +5[/math]	[math]5[/math]	[math]n_3[/math]	[math]shift\ 3[/math]	Перенос [math]"n_3"[/math]. Переход в [math]3[/math] состояние.
[math]\$[/math]	[math]0\ E1\ +5\ n_33[/math]	[math]3[/math]	[math]\$[/math]	[math]reduce\ 3[/math]	Свертка: [math]T \to \bf n[/math]. Удаление из стека [math]n_33[/math]. Переход в [math]5[/math] состояние. Добавление в стек [math]T7[/math]. Переход в [math]7[/math] состояние.
[math]\$[/math]	[math]0\ E1\ +5\ T7[/math]	[math]7[/math]	[math]\$[/math]	[math]reduce\ 1[/math]	Свертка: [math]E \to E + T[/math]. Удаление из стека [math]E1\ +5\ T7[/math]. Переход в [math]0[/math] состояние. Добавление в стек [math]E1[/math]. Переход в [math]1[/math] состояние.
[math]\$[/math]	[math]0\ E1[/math]	[math]1[/math]	[math]\$[/math]	[math]reduce\ 0[/math]	Так как свертка по нулевому правилу — осуществляем допуск.

См. также

• Предиктивный синтаксический анализ

Источники информации

• Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс, 2003. Стр. 301 - 326.
• Терехов Ан.А., Вояковская Н., Булычев Д., Москаль А. - Разработка компиляторов на платформе .NET - Восходящие анализаторы
• Б.К.Мартыненко. Языки и трансляции. Стр. 198 - 223
• Лекции по теории формальных языков, LR(0)-, SLR(1)-, LR(1)- и LALR(1)-анализ