LR(1)-разбор — различия между версиями
Xottab (обсуждение | вклад) |
Xottab (обсуждение | вклад) |
||
| Строка 93: | Строка 93: | ||
Псевдокод построения множеств $closure$ и $goto$, а также множества ситуаций $items$: | Псевдокод построения множеств $closure$ и $goto$, а также множества ситуаций $items$: | ||
<code> | <code> | ||
| − | + | Item[] closure(Item[] I): | |
'''bool''' changed | '''bool''' changed | ||
| − | + | Item[] J = I | |
'''repeat''' | '''repeat''' | ||
changed = '''false''' | changed = '''false''' | ||
| Строка 107: | Строка 107: | ||
</code> | </code> | ||
<code> | <code> | ||
| − | + | Item[] goto(Item[] I, X): | |
| − | + | Item[] J=$\varnothing$ | |
'''for''' $[A\rightarrow\alpha\cdot X\beta, a]\in I$ | '''for''' $[A\rightarrow\alpha\cdot X\beta, a]\in I$ | ||
J.add($[A\rightarrow\alpha X\cdot\beta, a]$) | J.add($[A\rightarrow\alpha X\cdot\beta, a]$) | ||
| Строка 114: | Строка 114: | ||
</code> | </code> | ||
<code> | <code> | ||
| − | + | Item[][] items($G'$): | |
'''bool''' changed | '''bool''' changed | ||
| − | + | Item[][] $C$ = $\{closure({S'\rightarrow\cdot S,\char36})\}$ | |
'''repeat''' | '''repeat''' | ||
changed = '''false''' | changed = '''false''' | ||
| − | '''for''' | + | '''for''' Item[] $I\subset C$ |
'''for''' $X \in symbols(G')$ <font color="green">//по всем символам грамматики</font> | '''for''' $X \in symbols(G')$ <font color="green">//по всем символам грамматики</font> | ||
'''if''' $goto(I,X)\neq\varnothing$ and $goto(I,X)\not\subset C$ | '''if''' $goto(I,X)\neq\varnothing$ and $goto(I,X)\not\subset C$ | ||
Версия 22:22, 14 сентября 2015
<wikitex> В некоторых случаях SLR-разбор может выдать неправильный результат. В таких случаях используют более сложные методы, такие как LR(1) и LALR-разбор. Рассмотрим первый из них. </wikitex>
Содержание
Отличия от SLR-разбора
<wikitex> Основным отличием LR(1)-разбора от SLR-разбора является использование предпросмотра (англ. lookahead) символов.
Приведём пример ситуации, в которой SLR-разбор не справится с задачей:
Рассмотрим грамматику вида: $ S \to L=R \mid R \\ L \to *R \mid id \\ R \to L $
Покажем её канонический LR(0)-набор:
| $I_0$ | $I_1$ | $I_2$ | $I_3$ | $I_4$ | $I_5$ | $I_6$ | $I_7$ | $I_8$ | $I_9$ |
|---|---|---|---|---|---|---|---|---|---|
|
$S' \to \cdot S \\ S \to \cdot L = R \\ S \to \cdot R \\ L \to \cdot * R \\ L \to \cdot id \\ R \to \cdot L$ |
$S' \to S \cdot$ |
$S \to L \cdot = R \\ R \to L \cdot$ |
$S \to R \cdot$ |
$L \to * \cdot R \\ R \to \cdot L \\ L \to \cdot * R \\ L \to \cdot id$ |
$L \to id \cdot$ |
$S \to L = \cdot R \\ R \to \cdot L \\ L \to \cdot * R \\ L \to \cdot id$ |
$L \to * R \cdot$ |
$R \to L \cdot$ |
$S \to L = R \cdot$ |
Рассмотрим ситуацию $I_2$. Если SLR-парсер находится в $I_2$ и очередной входной символ равен $=$, то парсер выполняет свёртку в соответствии с продукцией $R \to L$, что неверно, т.к. в этой грамматике не выводится выражение $R=\ldots$ и парсер должен был выполнить перенос, а не свёртку.
Чтобы решить эту проблему, необходимо хранить в ситуации больший объём информации, который позволит не делать таких ошибочных свёрток. </wikitex>
Канонические LR(1)-ситуации
<wikitex> Основная идея заключается в том, чтобы хранить в ситуациях больше информации, чтобы не производить некорректных свёрток. Добавим в ситуацию второй компонент: терминальный символ. Таким образом, LR(1)-ситуации будут выглядеть следующим образом:
$[A\rightarrow\alpha\cdot\beta, a]$, где первая часть — продукция, а вторая — терминал или маркер конца входной строки $\char36$. Здесь $a$ называется предпросмотром (англ. lookahead) ситуации, а число 1 в LR(1) означает его длину. Теперь мы будем выполнять свёртку в соответствии с продукцией $A\rightarrow\alpha$, только в том случае, если находимся в ситуации $[A\rightarrow\alpha\cdot\beta, a]$ и $a$ — входной символ.
| Определение: |
| Назовём LR(1)-ситуацию $[A\rightarrow\alpha\cdot\beta, a]$ допустимой (англ. valid) для активного префикса $\gamma$, если существует правое порождение $S\Rightarrow^{*}\delta A w\Rightarrow\delta\alpha\beta w$, где верно одно из трёх: либо $\gamma=\delta\alpha$, либо $a$ является первым символом $w$, либо$w=\varepsilon$ и $a=\char36$. |
</wikitex>
Построение множеств LR(1)-ситуаций
<wikitex> Метод построения похож на метод для $LR(0)$-разбора, с двумя изменёнными функциями: $closure(I)$ — замыкание множества ситуаций, и $goto(X,I)$ — функция переходов в автомате по символу $X$.
| Лемма: |
$$\forall{b} \mid b\in FIRST(\beta\alpha): [A\rightarrow\alpha\cdot B\beta, a]\in I\Rightarrow [B\rightarrow\cdot\gamma, b]\in closure(I)$$
Другими словами, при построении замыкания вторая часть добавленных ситуаций должна принадлежать $FIRST(\beta\alpha)$ |
| Доказательство: |
|
Рассмотрим ситуацию вида $[A\rightarrow\alpha\cdot B\beta, a]$ в множестве ситуаций, допустимых для некоторого активного префикса $\gamma$. Тогда существует правое порождение $S\Rightarrow^{*}\delta Aax\Rightarrow\delta\alpha B\beta ax$, где $\gamma=\delta\alpha$. Предположим, что $\beta ax$ порождает строку терминалов $by$. Тогда для каждой продукции вида $\forall{B\rightarrow\eta}\exists{\eta}$ мы имеем порождение $ S\Rightarrow^{*}\delta Bby\Rightarrow\delta\eta by$. Таким образом, $[B\rightarrow\cdot\eta,b]$ является допустимым для $\gamma$. Заметим, что $b$ может быть первым терминалом, порожденным из $\beta$, либо, возможно что $\beta$ порождает $\varepsilon$ слева: $\beta ax\Rightarrow^{*}by$, следовательно $b=a$. Таким образом, $b\in FIRST(\beta ax)$. Поскольку $x$ не может содержать первый терминал из $by$, то $FIRST(\beta ax)=FIRST(\beta a)$ Значит, $b\in FIRST(\beta a)$. |
</wikitex>
Псевдокод
<wikitex>
Псевдокод построения множеств $closure$ и $goto$, а также множества ситуаций $items$:
Item[] closure(Item[] I):
bool changed
Item[] J = I
repeat
changed = false
for $[A\rightarrow\alpha\cdot B\beta, a]\in I$
for $(B\rightarrow\gamma)\in G'$
for $b\in FIRST(\beta\alpha)$
J.add($[B\rightarrow\cdot\gamma,b]$)
changed = true
until not changed
return J
Item[] goto(Item[] I, X):
Item[] J=$\varnothing$
for $[A\rightarrow\alpha\cdot X\beta, a]\in I$
J.add($[A\rightarrow\alpha X\cdot\beta, a]$)
return $closure(J)$
Item[][] items($G'$):
bool changed
Item[][] $C$ = $\{closure({S'\rightarrow\cdot S,\char36})\}$
repeat
changed = false
for Item[] $I\subset C$
for $X \in symbols(G')$ //по всем символам грамматики
if $goto(I,X)\neq\varnothing$ and $goto(I,X)\not\subset C$
C.add($goto(I,X)$)
changed = true
until not changed
return C
</wikitex>
Пример
<wikitex> Рассмотрим следующую грамматику $G'$:
- $S'\rightarrow S$
- $S\rightarrow CC$
- $S\rightarrow cC|d$
Запустим процедуру $items(G')$. Она начинается с вычисления $closure([S\rightarrow S', \char36])$. Это правило вида $[A\rightarrow\alpha\cdot B\beta, a]$, где $A=S';\alpha=\varepsilon;B=S;\beta=\varepsilon;a=\char36$. Т.к. в таком случае $FIRST(\beta\alpha) = {\char36}$, то мы добавим только правило $[S\rightarrow\cdot CC,\char36]$.
Продолжив вычислять замыкание таким образом, мы добавим во множество ситуаций $[C\rightarrow\cdot C, c]$, $C\rightarrow\cdot C, d]$, $C\rightarrow\cdot d, c]$, и $C\rightarrow\cdot d, d]$. Т.к. ни одна из новых ситуаций не имеет вид $[A\rightarrow\alpha\cdot B\beta, a]$ (справа от точки во всех ситуациях терминалы), то функция $closure$ завершает свою работу и начальное множество ситуаций в данном случае равно:
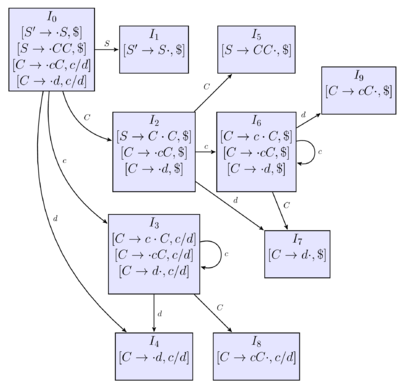
$$I_0: \{[S'\rightarrow \cdot S, \char36],[S\rightarrow\cdot CC,\char36],[C\rightarrow\cdot C, c/d],[C\rightarrow\cdot d, c/d]\}$$ Следующим шагом процедуры $items$ будет вычисление функции переходов автомата $goto(I_0,X)$ для всех символов $X$ грамматики $G'$:
При $X=S$: $$closure({[S'\rightarrow S\cdot,\char36]}) = \varnothing$$ Мы не добавили ни одной ситуации, т.к. точка является крайней справа. Таким образом, $$I_1: \{[S'\rightarrow S\cdot,\char36]\}$$ При $X=C$: $$I_2 = closure(\{[S\rightarrow C\cdot C,\char36]\})$$ $$I_2 = \{[S\rightarrow C\cdot C,\char36],[C\rightarrow\cdot cC,\char36],[C\rightarrow\cdot d,\char36]\}$$ При $X=c$: $$I_3 = closure(\{[C\rightarrow c\cdot C,c/d]\})$$ $$I_3 = \{[C\rightarrow c\cdot C,c/d],[C\rightarrow\cdot cC,c/d],[C\rightarrow\cdot d,c/d]\}$$ При $X=d$: $$I_4 = closure(\{[C\rightarrow d\cdot ,c/d]\})$$ $$I_4 = \{[C\rightarrow d\cdot,c/d]\}$$ На этом завершается выполнение цикла из процедуры $items$ для $I_0$. $$goto(I_1, *)=\varnothing$$ $$I_5 = goto(I_2, C) = closure(\{[S\rightarrow CC\cdot,\char36]\})=\{[S\rightarrow CC\cdot,\char36]\}$$ $$I_6 = goto(I_2, c) = closure(\{[C\rightarrow c\cdot C,\char36]\})$$ $$I_6=\{[C\rightarrow c\cdot C,\char36],[C\rightarrow \cdot cC,\char36],[C\rightarrow \cdot d,\char36]\}$$ Обратим внимание, что $I_6$ отличается от $I_3$ только правыми частями ситуаций. Такое явление является частым в LR(1)-анализе, из-за него результирующая таблица будет неоправданно большой. LALR-анализ борется с этим явлением. Продолжим: $$I_7 = goto(I_2, d) = closure(\{[C\rightarrow d\cdot ,\char36]\}) = \{[C\rightarrow d\cdot ,\char36]\}$$ На этом рассмотрение $goto(I_2)$ завершено, переходим к $goto(I_3)$: $$I_8 = goto(I_3, C) = closure(\{[C\rightarrow cC\cdot ,c/d]\}) = \{[C\rightarrow cC\cdot ,c/d]\}$$ В множествах $I_4$ и $I_5$ все ситуации имеют точки в крайнем положении справа, следовательно эти множества не имеют $goto$ $$goto(I_6, c) = I_6$$ $$goto(I_6, d) = I_7$$ $$I_9 = goto(I_6, C) = \{[C\rightarrow cC\cdot,\char36]\}$$ Остальные множества ситуаций не дают нам значений $goto$, процедура $items$ завершает работу. </wikitex>
Канонические LR(1)-таблицы
Алгоритм
// вход: — расширенная грамматика // выход: таблица канонического -анализа с функциями и function // множество канонических ситуаций для "ошибка" foreach if здесь — терминал "перенос " if && "свертка " if "принятие" if
Если в процессе построения обнаружатся конфликтующие действия — это значит, что грамматика не принадлежит классу LR(1)
Таблица, построенная в результате применения алгоритм называется канонической таблицей LR(1)-анализа.
Пример
<wikitex> Рассмотрим следующую грамматику $G$:
- $S\rightarrow CC$
- $C\rightarrow cC$
- $C\rightarrow d$
Приведем каноническую таблицу синтаксического анализа для этой грамматики:
| Состояние | $ACTION$ | $goto$ | |||
|---|---|---|---|---|---|
| $c$ | $d$ | $\char36$ | $S$ | $C$ | |
| $0$ | $s3$ | $s4$ | $1$ | $2$ | |
| $1$ | ok | ||||
| $2$ | $s6$ | $s7$ | $5$ | ||
| $3$ | $s3$ | $s4$ | $8$ | ||
| $4$ | $r1$ | $r3$ | |||
| $5$ | $r1$ | ||||
| $6$ | $s6$ | $s7$ | $9$ | ||
| $7$ | $r3$ | ||||
| $8$ | $r2$ | $r2$ | |||
| $9$ | $r2$ | ||||
</wikitex>
Источники информации
- Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс, 2003. Стр. 331-338.