Гамма-алгоритм — различия между версиями
Анна (обсуждение | вклад) (→Инициализация) |
Анна (обсуждение | вклад) |
||
| Строка 114: | Строка 114: | ||
|id=lemma1 | |id=lemma1 | ||
|about=1 | |about=1 | ||
| − | |statement=Конфликтующие сегменты <tex>S_{1}</tex> и <tex>S_{2}</tex> обладают следующим свойством: если <tex>|\Gamma(S_{1})| \ | + | |statement=Конфликтующие сегменты <tex>S_{1}</tex> и <tex>S_{2}</tex> обладают следующим свойством: если <tex>|\Gamma(S_{1})| \geqslant 2</tex> и <tex>|\Gamma(S_{2})| \geqslant 2</tex>, то <tex>\Gamma(S_{1}) = \Gamma(S_{2}) = 2</tex>. |
|proof=Сначала докажем, что <tex>\Gamma(S_{1}) = \Gamma(S_{2})</tex>. Предположим противное. Тогда по условию леммы найдутся три различные грани <tex>\Gamma_{1}, \Gamma_{2}</tex> и <tex>\Gamma_{3}</tex> такие, что <tex>\Gamma_{1} \in \Gamma(S_{1}), \Gamma_{2} \in \Gamma(S_{2}), \Gamma_{3} \in Q = \Gamma(S_{1}) \cap \Gamma(S_{2}) \neq \emptyset</tex>. Тогда любые цепи <tex>L_{1} \subset S_{1}</tex> и <tex>L_{2} \subset S_{2}</tex> укладываются в <tex>\Gamma_{1}</tex> и <tex>\Gamma_{2}</tex> соответственно. Но это значит, что любая пара цепей <tex>L_{1}</tex> и <tex>L_{2}</tex> одновременно укладывается вне грани <tex>\Gamma_{3}</tex>. Следовательно, они одновременно укладываются и внутри грани <tex>\Gamma_{3}</tex>, причем без пересечений. Но это противоречит тому, что <tex>S_{1}</tex> и <tex>S_{2}</tex> {{---}} конфликтующие сегменты. Таким образом, <tex>\Gamma(S_{1}) = \Gamma(S_{2})</tex>. | |proof=Сначала докажем, что <tex>\Gamma(S_{1}) = \Gamma(S_{2})</tex>. Предположим противное. Тогда по условию леммы найдутся три различные грани <tex>\Gamma_{1}, \Gamma_{2}</tex> и <tex>\Gamma_{3}</tex> такие, что <tex>\Gamma_{1} \in \Gamma(S_{1}), \Gamma_{2} \in \Gamma(S_{2}), \Gamma_{3} \in Q = \Gamma(S_{1}) \cap \Gamma(S_{2}) \neq \emptyset</tex>. Тогда любые цепи <tex>L_{1} \subset S_{1}</tex> и <tex>L_{2} \subset S_{2}</tex> укладываются в <tex>\Gamma_{1}</tex> и <tex>\Gamma_{2}</tex> соответственно. Но это значит, что любая пара цепей <tex>L_{1}</tex> и <tex>L_{2}</tex> одновременно укладывается вне грани <tex>\Gamma_{3}</tex>. Следовательно, они одновременно укладываются и внутри грани <tex>\Gamma_{3}</tex>, причем без пересечений. Но это противоречит тому, что <tex>S_{1}</tex> и <tex>S_{2}</tex> {{---}} конфликтующие сегменты. Таким образом, <tex>\Gamma(S_{1}) = \Gamma(S_{2})</tex>. | ||
| − | Теперь покажем, что <tex>|Q| = 2</tex>. Доказательство снова поведем методом от противного. Пусть <tex>|Q| \ | + | Теперь покажем, что <tex>|Q| = 2</tex>. Доказательство снова поведем методом от противного. Пусть <tex>|Q| \geqslant 3</tex>. Тогда снова существует три различные грани <tex>\Gamma_{1}, \Gamma_{2}</tex> и <tex>\Gamma_{3} \in Q</tex>. Аналогичными рассуждениями снова приходим к противоречию с тем, что <tex>S_{1}</tex> и <tex>S_{2}</tex> {{---}} конфликтующие сегменты. |
}} | }} | ||
| Строка 141: | Строка 141: | ||
|id=lemma2 | |id=lemma2 | ||
|about=2 | |about=2 | ||
| − | |statement=Если результатом некоторого шага работы гамма-алгоритма является частичная укладка <tex>G'</tex> планарного графа <tex>G</tex> такая, что <tex>|\Gamma(S)| \ | + | |statement=Если результатом некоторого шага работы гамма-алгоритма является частичная укладка <tex>G'</tex> планарного графа <tex>G</tex> такая, что <tex>|\Gamma(S)| \geqslant 2</tex> для любого сегмента <tex>S</tex> относительно <tex>G'</tex>, то <tex>A(G')</tex> {{---}} [[Двудольные графы и раскраска в 2 цвета|двудольный граф]]. |
|proof=Докажем от противного. Пусть <tex>A(G')</tex> {{---}} не двудольный. Тогда по [http://neerc.ifmo.ru/wiki/index.php?title=%D0%94%D0%B2%D1%83%D0%B4%D0%BE%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%B3%D1%80%D0%B0%D1%84%D1%8B_%D0%B8_%D1%80%D0%B0%D1%81%D0%BA%D1%80%D0%B0%D1%81%D0%BA%D0%B0_%D0%B2_2_%D1%86%D0%B2%D0%B5%D1%82%D0%B0#.D0.A2.D0.B5.D0.BE.D1.80.D0.B5.D0.BC.D0.B0_.D0.9A.D0.B5.D0.BD.D0.B8.D0.B3.D0.B0 теореме Кенинга] в нем есть цикл нечетной длины. Этому циклу соответствует некоторая последовательность сегментов <tex>S_{1}, S_{2}, \cdots S_{2m+1}, S_{1}</tex> относительно <tex>G'</tex>, в которой каждые соседние сегменты конфликтующие по определению. По лемме 1 <tex>\Gamma(S_{i}) = \{\Gamma_{1}, \Gamma_{2}\}, i \in \{1 \cdots 2m+1\}</tex>. Так как <tex>G'</tex> {{---}} частичная укладка графа, то все сегменты <tex>S_{1}, S_{2}, \cdots S_{2m+1}</tex> могут быть уложены. А так как соседние сегменты этой последовательности конфликтующие, то они должны быть уложены в разные грани, что невозможно, так как число сегментов в последовательности нечетное. Получили противоречие. Следовательно, <tex>A(G')</tex> {{---}} двудольный. | |proof=Докажем от противного. Пусть <tex>A(G')</tex> {{---}} не двудольный. Тогда по [http://neerc.ifmo.ru/wiki/index.php?title=%D0%94%D0%B2%D1%83%D0%B4%D0%BE%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%B3%D1%80%D0%B0%D1%84%D1%8B_%D0%B8_%D1%80%D0%B0%D1%81%D0%BA%D1%80%D0%B0%D1%81%D0%BA%D0%B0_%D0%B2_2_%D1%86%D0%B2%D0%B5%D1%82%D0%B0#.D0.A2.D0.B5.D0.BE.D1.80.D0.B5.D0.BC.D0.B0_.D0.9A.D0.B5.D0.BD.D0.B8.D0.B3.D0.B0 теореме Кенинга] в нем есть цикл нечетной длины. Этому циклу соответствует некоторая последовательность сегментов <tex>S_{1}, S_{2}, \cdots S_{2m+1}, S_{1}</tex> относительно <tex>G'</tex>, в которой каждые соседние сегменты конфликтующие по определению. По лемме 1 <tex>\Gamma(S_{i}) = \{\Gamma_{1}, \Gamma_{2}\}, i \in \{1 \cdots 2m+1\}</tex>. Так как <tex>G'</tex> {{---}} частичная укладка графа, то все сегменты <tex>S_{1}, S_{2}, \cdots S_{2m+1}</tex> могут быть уложены. А так как соседние сегменты этой последовательности конфликтующие, то они должны быть уложены в разные грани, что невозможно, так как число сегментов в последовательности нечетное. Получили противоречие. Следовательно, <tex>A(G')</tex> {{---}} двудольный. | ||
| Строка 161: | Строка 161: | ||
1. Существует сегмент <tex>S</tex> для которого есть единственная вмещающая грань <tex>\Gamma</tex>, то есть <tex>|\Gamma(S)| = 1</tex>. Так как только грани <tex>\Gamma</tex> принадлежат все контактные вершины <tex>S</tex>, то укладка этого сегмента в эту грань неизбежна. Это значит, что помещая любую цепь <tex>L \subset S</tex>, снова получим частичную укладку графа. | 1. Существует сегмент <tex>S</tex> для которого есть единственная вмещающая грань <tex>\Gamma</tex>, то есть <tex>|\Gamma(S)| = 1</tex>. Так как только грани <tex>\Gamma</tex> принадлежат все контактные вершины <tex>S</tex>, то укладка этого сегмента в эту грань неизбежна. Это значит, что помещая любую цепь <tex>L \subset S</tex>, снова получим частичную укладку графа. | ||
| − | 2. Для любого сегмента <tex>S</tex> <tex>|\Gamma(S)| \ | + | 2. Для любого сегмента <tex>S</tex> <tex>|\Gamma(S)| \geqslant 2</tex>. Построим граф <tex>A(G'_{k-1})</tex>, который по лемме 2 является двудольным. Рассмотрим его связную компоненту <tex>K</tex>, которая содержит не менее двух вершин. Граф <tex>K</tex> также является двудольным. По лемме 1 для любого сегмента <tex>S \in K</tex> справедливо <tex>\Gamma(S) = \{\Gamma_{1}, \Gamma_{2}\}</tex>. Так как граф <tex>K</tex> двудольный, то мы можем по очереди помещать сегменты <tex>K</tex> в разные грани, причем конфликтующих сегментов не возникнет в силу четности всех циклов в графе. Результатом будет частичная укладка графа. |
Таким образом, на каждом шаге мы получаем частичную укладку графа, что доказывает корректность гамма-алгоритма. | Таким образом, на каждом шаге мы получаем частичную укладку графа, что доказывает корректность гамма-алгоритма. | ||
Версия 23:14, 19 ноября 2015
| Задача: |
| Определить, является ли граф планарным, и, если да, произвести его плоскую укладку. |
Существует теорема Понтрягина-Куратовского, которая говорит, что граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных или . Но этот критерий очень трудно проверить на практике, поэтому данная теорема представляет лишь теоретический интерес.
Чтобы проверить планарность графа и произвести его плоскую укладку, удобно пользоваться гамма-алгоритмом.
Содержание
Входные данные
На вход алгоритму подаются графы со следующими свойствами:
Если нарушено свойство 1, то граф нужно укладывать отдельно по компонентам связности. Если нарушено свойство 2, то граф — дерево и нарисовать его плоскую укладку тривиально.
Более подробно рассмотрим случай, когда в графе нарушено свойство 3. Сначала все мосты нужно убрать, далее произвести отдельную укладку всех компонент следующим образом: уложим одну компоненту связности, а следующую компоненту, связанную с первой в графе мостом, будем рисовать в той грани, в которой лежит вершина, принадлежащая мосту. Иначе может сложиться ситуация, когда концевая вершина моста будет находиться внутри плоского графа, а следующая компонента — снаружи. Таким образом мы сможем соединить мостом нужные вершины. Далее будем так поступать с каждой новой компонентой.
Описание алгоритма
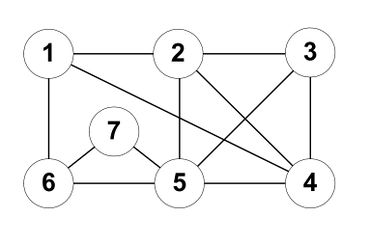
Рассмотрим работу алгоритма, параллельно разбирая на примере каждый шаг. Пусть дан граф (рис. 1).
Инициализация
Первый этап - инициализация алгоритма.
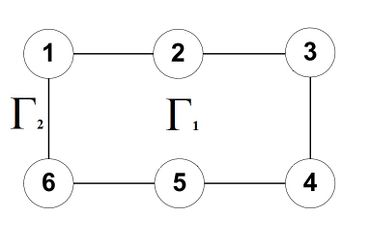
В графе выбирается любой простой цикл и производится его укладка на плоскость. Пусть в примере это будет цикл . После его укладки получаем две грани: и (рис. 2).
Уже уложенную во время работы алгоритма часть будем обозначать . В примере сейчас — выбранный цикл .
Общий шаг
Второй этап - общий шаг.
Построим множество сегментов. Каждый сегмент относительно уже построенного представляет собой одно из двух:
- ребро, оба конца которого принадлежат , но само оно не принадлежит ,
- связную компоненту графа , дополненную всеми ребрами графа такими, у которых один из концов принадлежит связной компоненте, а второй принадлежит графу .
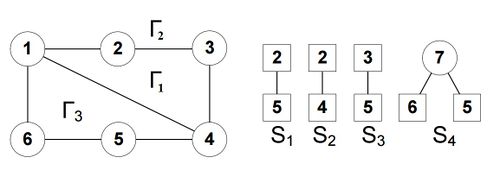
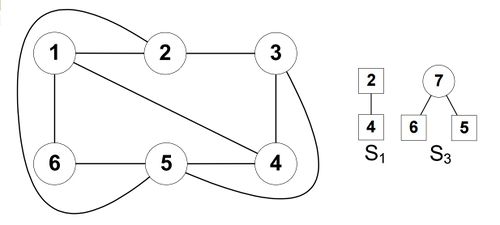
Вершины, одновременно принадлежащие и какому-либо сегменту, назовем контактными. На рис. 3 изображены сегменты для нашего примера. Контактные вершины обведены в квадрат.
Пусть в каком-то сегменте нет ни одной контактной вершины. В таком случае граф до выделения был несвязным, что противоречит условию. Пусть контактная вершина в сегменте только одна. Это значит, что в графе был мост, чего быть не может так же по условию. Таким образом, в каждом сегменте имеется не менее двух контактных вершин. Соответственно, в каждом сегменте есть цепь между любой парой контактных вершин.
Пусть грань вмещает сегмент , если номера всех контактных вершин принадлежат этой грани, . Очевидно, таких граней может быть несколько. Множество таких граней обозначим , а их число — .
Итак, рассмотрим все сегменты и для каждого определим число . Если найдется такой номер , что , то граф не планарен, алгоритм завершает работу. Иначе выбираем такой сегмент , для которого число минимально. Если таких сегментов несколько, можно выбрать любой из них. Найдем в этом сегменте цепь между двумя контактными вершинами и уложим ее в любую грань из множества , совместив контактные вершины сегмента с соответствующими вершинами грани. Выбранная грань разобьется на две. Выбранный сегмент после того, как из него взяли цепь, либо исчезнет, либо распадется на меньшие части, в которых будут новые контактные вершины, ведущие к вершинам обновленного .
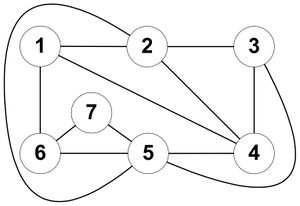
В примере для любого : , то есть . Следовательно, можем выбрать любой . Пусть это будет сегмент . В нем есть цепь . Вставим эту цепь в грань , например, и этот сегмент исчезнет. После укладки цепи граф и сегменты будут выглядеть так (рис. 4):
Третий и последующие этапы аналогичны второму. Повторять вышеуказанные действия нужно либо до тех пор, пока не будет получена плоская укладка, то есть множество сегментов не останется пустым, либо пока не будет получено, что граф не планарен.
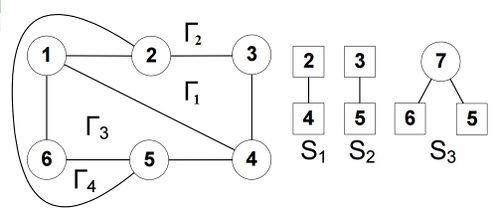
Разберем пример до конца. Повторим снова общий шаг. Теперь , . Возьмем . В ней цепь , которую мы уложим в грань , после чего этот сегмент исчезнет. Теперь картина будет следующая (рис. 5):
На следующем шаге , . Выбираем сегмент , содержащий цепь . Уложим ее в грань , после чего этот сегмент снова исчезнет (рис. 6).
Теперь , а . Уложим сначала цепь из первого сегмента, он пропадет, потом уложим цепь из третьего. В результате граф будет полностью уложен на плоскость, множество сегментов останется пустым (рис. 7).
Таким образом, мы получили плоскую укладку исходного графа .
Опишем алгоритм коротко и формально:
- Инициализация. Выбирается простой цикл в исходном графе и изображается на плоскости.
- Общий шаг. Этот шаг повторяется до тех пор, пока граф не будет уложен или пока не будет получено, что граф не планарен.
- строится множество сегментов
- для каждого сегмента вычисляется величина . Если существует : , то граф не планарен, алгоритм завершает работу
- выбирается сегмент с минимальным числом
- в этом сегменте выбирается цепь между двумя контактными вершинами
- эта цепь укладывается в любую грань, вмещающую данный сегмент
- Либо получена плоская укладка графа, либо граф оказался не планарен.
Доказательство корректности гамма-алгоритма
Перед доказательством корректности приведем ряд важных вспомогательных лемм.
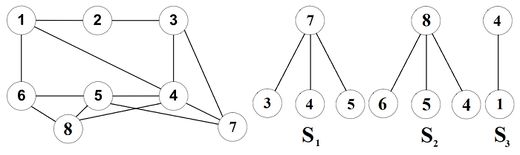
Пусть два сегмента и называются конфликтующими относительно уже уложенной части, если:
- грань вмещает каждый из сегментов и
- в этих сегментах есть две цепи между контактными вершинами и соответственно такие, что их невозможно уложить в одну грань без пересечения
Например, на рис. 1 конфликтующими являются сегменты и .
| Лемма (1): |
Конфликтующие сегменты и обладают следующим свойством: если и , то . |
| Доказательство: |
|
Сначала докажем, что . Предположим противное. Тогда по условию леммы найдутся три различные грани и такие, что . Тогда любые цепи и укладываются в и соответственно. Но это значит, что любая пара цепей и одновременно укладывается вне грани . Следовательно, они одновременно укладываются и внутри грани , причем без пересечений. Но это противоречит тому, что и — конфликтующие сегменты. Таким образом, . Теперь покажем, что . Доказательство снова поведем методом от противного. Пусть . Тогда снова существует три различные грани и . Аналогичными рассуждениями снова приходим к противоречию с тем, что и — конфликтующие сегменты. |
Замечание. Пусть имеется множество сегментов таких, что они удовлетворяют следующей схеме: есть первый сегмент , второй , который конфликтует с , третий , который конфликтует с , но не с , и так далее, причем каждый из них укладывается в две грани. Тогда из леммы 1 следует, что эти грани являются общими для всех сегментов множества и можно укладывать их следующим образом: цепь укладывается в первую грань , цепь — во вторую , — снова в и так для всех элементов множества. Если цепочка сегментов замыкается в цикл четной длины, то проблем никаких нет. Если длина цикла нечетная, то два последних конфликтующих сегмента нужно будет уложить в одну грань без пересечений, что по определению невозможно. Следовательно, получить плоскую укладку нельзя.
| Определение: |
| Частичной укладкой планарного графа называется граф, который можно получить из какой-либо укладки графа на плоскости путем удаления некоторых ребер и вершин. |
Таким образом во всякую частичную укладку планарного графа можно уложить оставшуюся часть, а именно недостающие вершины и ребра графа .
Построим некоторый служебный граф по следующей схеме: каждому сегменту в сопоставим некоторую вершину в , причем две вершины будут смежны тогда и только тогда, когда соответствующие им сегменты являются конфликтующими.
Например, для графа на рис. 1 служебный граф будет иметь вид (рис. 2):
| Лемма (2): |
Если результатом некоторого шага работы гамма-алгоритма является частичная укладка планарного графа такая, что для любого сегмента относительно , то — двудольный граф. |
| Доказательство: |
| Докажем от противного. Пусть — не двудольный. Тогда по теореме Кенинга в нем есть цикл нечетной длины. Этому циклу соответствует некоторая последовательность сегментов относительно , в которой каждые соседние сегменты конфликтующие по определению. По лемме 1 . Так как — частичная укладка графа, то все сегменты могут быть уложены. А так как соседние сегменты этой последовательности конфликтующие, то они должны быть уложены в разные грани, что невозможно, так как число сегментов в последовательности нечетное. Получили противоречие. Следовательно, — двудольный. |
| Теорема (О корректности гамма-алгоритма): |
Гамма-алгоритм корректен, то есть если — планарный граф, то результатом каждого шага гамма-алгоритма является частичная укладка . |
| Доказательство: |
|
Докажем индукцией по числу шагов. База индукции: полученный на этапе инициализации граф является простым циклом, он будет присутствовать в любой укладке графа . Таким образом, является частичной укладкой. Шаг индукции: пусть граф , полученный на -м шаге работы алгоритма, является частичной укладкой. Докажем, что граф , полученный на -м шаге присоединением цепи , также является частичной укладкой. Заметим, что на текущем шаге нет такого сегмента относительно , для которого бы выполнялось равенство , так как в противном случае существовала бы цепь этого сегмента, контактные вершины которой принадлежали бы разным граням и укладка которой была бы невозможна. Следовательно, нельзя было бы уложить ,что противоречит тому, что — планарный граф. Значит, мы можем рассматривать только следующие два случая: 1. Существует сегмент для которого есть единственная вмещающая грань , то есть . Так как только грани принадлежат все контактные вершины , то укладка этого сегмента в эту грань неизбежна. Это значит, что помещая любую цепь , снова получим частичную укладку графа. 2. Для любого сегмента . Построим граф , который по лемме 2 является двудольным. Рассмотрим его связную компоненту , которая содержит не менее двух вершин. Граф также является двудольным. По лемме 1 для любого сегмента справедливо . Так как граф двудольный, то мы можем по очереди помещать сегменты в разные грани, причем конфликтующих сегментов не возникнет в силу четности всех циклов в графе. Результатом будет частичная укладка графа. Таким образом, на каждом шаге мы получаем частичную укладку графа, что доказывает корректность гамма-алгоритма. |
Следствие: Если граф планарный, то гамма-алгоритм строит его плоскую укладку.
Следствие: Если на каком-то шаге встретился сегмент , для которого нет вмещающей грани, то граф непланарный.