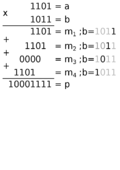Матричный умножитель — различия между версиями
(→Умножение в бинарной системе: изменен рисунок mult_bin_simple.png. Внесены редакторские правки в текст.) |
(→Умножение в бинарной системе) |
||
| Строка 8: | Строка 8: | ||
[[Файл:Матричный_умножитель_2.PNG|420px|thumb|right]] | [[Файл:Матричный_умножитель_2.PNG|420px|thumb|right]] | ||
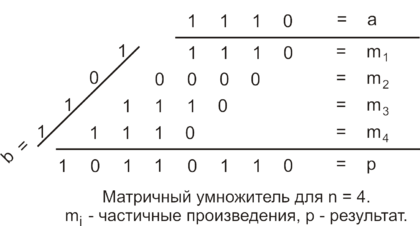
Умножение в бинарной системе счисления происходит точно так же, как в десятичной - по схеме "умножения столбиком". | Умножение в бинарной системе счисления происходит точно так же, как в десятичной - по схеме "умножения столбиком". | ||
| − | Если множимое - <tex>m</tex> разрядное, а множитель -<tex>n</tex> разрядный, то для формирования произведения требуется вычислить <tex>n</tex> частичных <tex>m</tex> разрядных произведений и сложить их между собой | + | Если множимое - <tex>m</tex> разрядное, а множитель -<tex>n</tex> разрядный, то для формирования произведения требуется вычислить <tex>n</tex> частичных <tex>m</tex> разрядных произведений и сложить их между собой. |
| − | |||
==== Вычисление частичных произведений ==== | ==== Вычисление частичных произведений ==== | ||
Версия 18:29, 18 января 2016
Содержание
Определение
Матричный умножитель — цифровая схема, осуществляющая умножение двух чисел c помощью двоичного каскадного сумматора.
Принцип работы
Умножение в бинарной системе
Умножение в бинарной системе счисления происходит точно так же, как в десятичной - по схеме "умножения столбиком". Если множимое - разрядное, а множитель - разрядный, то для формирования произведения требуется вычислить частичных разрядных произведений и сложить их между собой.
Вычисление частичных произведений
Для формирования частичного произведения, кроме операции умножения на один разряд, требуется осуществлять его сдвиг влево на число разрядов, соответствующее весу разряда множителя. Сдвиг можно осуществить простым соединением соответствующих разрядов частичных произведений к необходимым разрядам двоичного сумматора.
Матричный умножитель вычисляет частичные произведения по формуле:
Суммирование частичных произведений
На этом этапе происходит сложение всех частичных произведений . В большинстве современных систем это происходит с помощью дерева Уоллеса.
Схема
Далее будем рассматривать умножение пяти разрядного и четырех разрядного чисел. Соответственно нам понадобится три пяти разрядных сумматора.
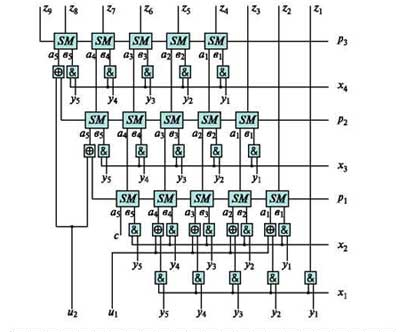
Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик, приведена на схеме. Формирование частичных произведений в этой схеме осуществляется посредством логических элементов “И”.
Помимо этого, рассматриваемая схема содержит шесть дополнительных двухвходовых элементов "исключающее ИЛИ" и два дополнительных входа . При этом в рабочем режиме на входы подаются сигналы логического "0".
Это нужно для работы теста проверяющего неисправности. Но это не относится к этой теме.
Работа схемы
Схема работает по достаточно простому принципу.
В начале первый разряд первого и первый разряд второго числа поступают на элемент "И" и результат сразу записывается в первый разряд произведения.
Дальше второй разряд первого числа снова поступает вместе с первым разрядом второго числа на элемент И и результат уже суммируется с произведение первого разряда первого числа и второго разряда второго числа и все это записывается во второй разряд произведения.
И дальше все продолжается по циклу.
То есть все произведения разрядов первого числа на разряд второго числа суммируются с произведением предыдущего разряда первого числа на разряд второго числа. И далее эта сумма так же суммируется, если только мы уже не получили нужный нам разряд произведения.
Проводники
Как мы можем видеть, — разряды первого числа, — разряды второго числа. проводники идут ко всем элементам "И", а идут каждый только к одному из пяти разрядных сумматоров . А на выходе мы имеем — разряды конечного числа.
"Матричный умножитель"
Если внимательно посмотреть на схему умножителя, то можно увидеть, что она образует матрицу, сформированную проводниками, по которым передаются разряды числа и числа . В точках пересечения этих проводников находятся логические элементы “И”. Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей.
Схемная сложность
Частичные произведения вычисляются за шагов. Сложение с вычислением переносов включает шаг. Последнее сложение можно выполнить за .
В итоге суммарное время работы:
Время работы схемы можно сократить, если сумматоры располагать не последовательно друг за другом, как это предполагается алгоритмом, приведенным на первом рисунке (общая схема), а суммировать частичные произведения попарно, затем суммировать пары частичных произведений и т.д. В этом случае время выполнения операции умножения значительно сократится.
Особенно заметен выигрыш в быстродействии при построении многоразрядных умножителей, однако ничего не бывает бесплатно. В обмен на быстродействие придётся заплатить увеличением разрядности сумматоров, а значит сложностью схемы.
Есть и более быстрые способы умножения двух чисел, например умножение с помощью дерева Уоллеса, которое работает .
Литература и источники
- Е. Угрюмов "Цифровая схемотехника" 2001г.
- Дк. Ф. Уэйкерли "Проектирование цифровых устройств, том 1." 2002г.
- М.И. Богданович "Цифровые интегральные микросхемы" 1996г.
- В.Л. Шило "Популярные цифровые микросхемы" 1988г.
- Кормен Т., Лейзерсон Ч., Ривест Р.. Алгоритмы: построение и анализ = Introduction to Algorithms / Пер. с англ. под ред. А. Шеня. — М.: МЦНМО, 2000. — 960 с. — ISBN 5-900916-37-5