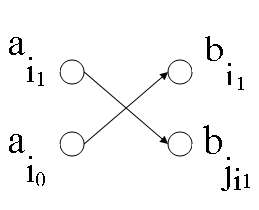|
|
| Строка 1: |
Строка 1: |
| − | '''Граф замен''' — специальный [[Основные определения теории графов|ориентированный двудольный граф]], фигурирующий в [[Теорема Эдмондса-Лоулера|теореме Эдмондса-Лоулера]]. | + | '''Граф замен''' (англ ''exchange graph'') {{---}} специальный [[Основные определения теории графов|ориентированный двудольный граф]], фигурирующий в [[Теорема Эдмондса-Лоулера|теореме Эдмондса-Лоулера]]. |
| | | | |
| | Пусть даны матроиды <tex>M_1 = \langle S, \mathcal{I}_1 \rangle</tex>, <tex>M_2 = \langle S, \mathcal{I}_2 \rangle</tex>, множество <tex>(\mathcal{I}_1 \cap \mathcal{I}_2)</tex>. Введем граф замен. | | Пусть даны матроиды <tex>M_1 = \langle S, \mathcal{I}_1 \rangle</tex>, <tex>M_2 = \langle S, \mathcal{I}_2 \rangle</tex>, множество <tex>(\mathcal{I}_1 \cap \mathcal{I}_2)</tex>. Введем граф замен. |
Версия 07:59, 13 апреля 2017
Граф замен (англ exchange graph) — специальный ориентированный двудольный граф, фигурирующий в теореме Эдмондса-Лоулера.
Пусть даны матроиды [math]M_1 = \langle S, \mathcal{I}_1 \rangle[/math], [math]M_2 = \langle S, \mathcal{I}_2 \rangle[/math], множество [math](\mathcal{I}_1 \cap \mathcal{I}_2)[/math]. Введем граф замен.
| Определение: |
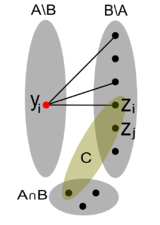
| Граф замен для двух матроидов [math]D_{M_1, M_2}(I)[/math] — граф, левой долей которого являются элементы множества [math]I[/math], правой — все остальные элементы [math]S[/math] и в котором проведены ребра [math](y, z): y \in I, z \in S \setminus I, I \setminus y \cup z \in \mathcal{I}_1[/math], а также [math](z', y'): y' \in I, z' \in S \setminus I, I \setminus y' \cup z' \in \mathcal{I}_2[/math] |
Пусть [math]X_1 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_1 \}, X_2 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_2 \}, P[/math] — кратчайший путь в [math]D_{M_1, M_2}(I)[/math] из [math]X_1[/math] в [math]X_2[/math]. Тогда алгоритм с помощью этого пути либо определяет максимальность набора [math]I[/math], либо позволяет найти набор большей мощности.
Граф замен
[math]D_{M_1, M_2}(I)[/math]Также существует граф замен для одного матроида.
| Определение: |
| Пусть дан матроид [math]M = (S, \mathcal{I})[/math] и независимый сет [math]I \in \mathcal{I}[/math]. Тогда граф замен [math]D_{M}(I)[/math] (или просто [math]D(I)[/math]) — это двудольный граф с долями [math]I[/math] и [math]S \setminus I[/math] с рёбрами между [math]y \in I[/math] и [math]x \in S \setminus I[/math] если [math] I - y + x \in \mathcal{I} [/math] |
| Лемма (о единственном паросочетании в подграфе замен, индуцированном кратчайшим путем): |
Пусть дан двудольный граф замен. В его правой доле можно выделить два подмножества вершин [math]X_1 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_1 \}, X_2 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_2 \}[/math]. Пусть [math]P[/math] — кратчайший путь из [math]X_1[/math] в [math]X_2[/math]. Рассмотрим сужение [math]G'[/math] графа [math]G[/math] на множество вершин, лежащих в пути [math]P[/math].
Тогда в [math]G'[/math] существует единственное полное паросочетание. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Строго говоря, утверждение теоремы не совсем корректно, так как в правой доле полученного графа [math]G'[/math] вершин на одну больше, чем в левой. Поэтому добавим в [math]G'[/math] фиктивную вершину и отнесем ее к левой доле. Пусть путь [math]P = (a_1, b_1, a_2, b_2, \ldots , a_k, b_k)[/math], где [math]a_1[/math] — фиктивная вершина (рис. 1).
Существование полного паросочетания очевидно — это ребра [math](a_i,b_i)[/math].
Предположим, что существует другое паросочетание [math](a_i, b_{j_i})[/math]. Тогда пусть [math]i_0 = \min \{ i \: \mid \: j_i \lt i \}[/math]. Обозначим [math]j_{i_0}[/math] как [math]i_1[/math]. Заметим, что [math]i_1 \lt i_0[/math] и поэтому не может быть [math]j_{i_1} \lt i_1[/math], ведь [math]i_0[/math] — минимальное из соответствующего множества. Так же невозможно [math]j_{i_1} = i_1[/math], поскольку тогда [math]a_{i_0}[/math] и [math]a_{i_1}[/math] имели бы одинаковую пару. Следовательно, [math]j_{i_1} \gt i_1[/math] (рис. 2). Это значит, что существует путь [math]P_1 = (a_1, b_1, \ldots, a_{i_1}, b_{j_{i_1}}, a_{j_{i_1} + 1}, \ldots, a_k, b_k )[/math] короче, чем [math]P[/math].
Противоречие. |
| [math]\triangleleft[/math] |
| Лемма (о паросочетании в графе замен): |
Пусть [math]M = \langle X,\mathcal{I} \rangle [/math] — матроид. Множества [math]A, B \in \mathcal{I}[/math] — независимы, причем [math]|A| = |B|[/math]. Тогда двудольный граф [math]D_{M}(\mathcal{I})[/math] содержит полное паросочетание на [math]A \bigtriangleup B[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Докажем по индукции для [math]|A \bigtriangleup B|[/math].
- База
- В случае, когда [math]|A \bigtriangleup B| = 0 [/math], имеем пустое паросочетание.
- Переход
- Считаем, что утверждение [math]|A \bigtriangleup B| = N[/math] — верно.
- Пусть [math]k = |A| = |B|[/math] и [math]|A \bigtriangleup B| \geqslant 1[/math].
- Рассмотрим матроид [math]M_1 = \langle X, \{ A \mid A \in \mathcal{I}, A \leqslant k \} \rangle[/math]. Множества [math]A, B \in \mathcal{I}[/math], [math]|A| = |B|[/math] и матроид [math]M_1[/math] не содержит множеств больших, чем [math]A[/math], а значит они являются базами для матроида [math]M_1[/math]. По сильной теореме о базах [math]\forall x \in A \setminus B: \exists y \in B \setminus A : (A \setminus x) \cup y \in \mathcal{I}[/math] и [math](B \setminus y) \cup x \in \mathcal{I}[/math] из этого следует, что множество [math]A' = A - x + y [/math] и [math]B' = B + x - y[/math] являются независимыми, а также базами [math]M_1[/math]. И их [math]|A' \bigtriangleup B'| \lt |A \bigtriangleup B|[/math]. Значит мы умеем переходить от [math]|A' \bigtriangleup B'| = N[/math] к [math]|A \bigtriangleup B| = N+1[/math]. По предположению индукции у [math] |A' \bigtriangleup B'|[/math] есть полное паросочетание.
- По теореме о базах [math]\forall x \in A \setminus B: \exists y \in B \setminus A : (A \setminus x) \cup y
\in \mathcal{I}[/math], следовательно по определению графа [math]D_M(A) \Rightarrow (x, y) \in D_M(A)[/math]. Тогда [math]N \cup {(x, y)}[/math] составляет полное паросочетание на [math]|A \bigtriangleup B|[/math], а значит индукционный переход справедлив.
|
| [math]\triangleleft[/math] |
Лемма о единственном паросочетании в графе замен
| Утверждение: |
Пусть двудольный граф [math]G[/math] содержит единственное полное паросочетание [math]M[/math]. Тогда можно упорядочить вершины левой [math](a_i \in A)[/math] и правой [math](b_i \in B)[/math] долей таким образом, что [math]\forall j \gt i : (a_i b_j) \notin G[/math]. При этом рёбра паросочетания будут иметь вид [math](a_i b_i)[/math]. |
| [math]\triangleright[/math] |
|
Индукция по [math]|A|[/math].
- База
- При [math]|A|=1[/math] утверждение очевидно.
- Переход
- Пусть [math]|A|=n\gt 1[/math] (для [math]|A|=n-1[/math] утверждение верно). Возьмем произвольную вершину в левой доли. Будем строить из неё чередующуюся цепь, добавляя по очереди ребро, входящее в [math]M[/math], и ребро, не входящее в [math]M[/math]. Заметим, что такой путь не содержит циклов (циклы нечётной длины невозможны, так как граф двудольный, циклы чётной длины отсутствуют из-за единственности паросочетания). Если последнее добавленное ребро не принадлежит [math]M[/math], то присоединим к цепи ребро из [math]M[/math], инцидентное последней вершине. Значит, построение цепи прервется только при добавлении ребра из [math]M[/math] при достижении вершины степени [math]1[/math].
Таким образом, последнее ребро в цепи имеет вид [math](ab) \in M[/math], где [math]a \in A, b \in B, \deg b = 1[/math]. Положим [math]a_n=a, b_n=b[/math]. Для [math]G \setminus \{a_n \cup b_n \}[/math] утверждение верно по предположению индукции. С другой стороны, так как [math]\deg b_n = 1[/math], то [math](a_i b_n) \notin G[/math] при [math]i\lt n[/math], поэтому для [math]j = n[/math] утверждение также верно.
|
| [math]\triangleleft[/math] |
| Лемма (о единственном паросочетании в графе замен): |
Дан матроид [math]M = \langle X,I \rangle [/math]. Пусть двудольный граф [math]G_M(A) = \{ (x, y) \mid x \in A, y \notin A, A \setminus x \cup y \in I \}[/math] содержит единственное полное паросочетание на [math]A \oplus B[/math], где [math]A\in I[/math] и [math]|A| = |B|[/math]. Тогда [math]B \in I[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
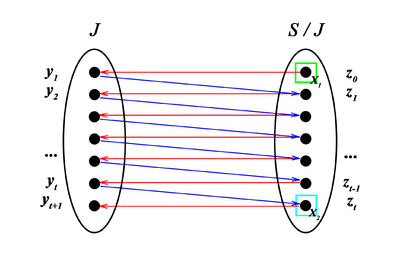
Упорядочим вершины левой [math](y_i \in A \setminus B)[/math] и правой [math](z_j \in B \setminus A)[/math] долей таким образом, что [math]\forall j \gt i : (y_i z_j) \notin G_M(A)[/math]. При таком упорядочивании ребра паросочетания имеют вид [math](y_i z_i)[/math].
Требуется доказать, что [math]B[/math] независимо. Предположим обратное. Пусть [math]B \notin I[/math], тогда существует цикл [math]C \subset B[/math].
Выберем минимальное [math]i[/math] такое, что [math]z_i \in C[/math]. Так как [math]\forall j \gt i : (y_i z_j) \notin G_M(A)[/math], то [math]A \setminus y_i \cup z_j \notin I[/math], следовательно, [math]C \setminus z_i \subset \langle A \setminus y_i \rangle [/math]. По свойствам замыкания 1 и 3 получаем:
[math]C \setminus z_i \subset \langle A \setminus y_i \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle \langle A \setminus y_i \rangle \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle[/math]
Так как [math]z_i \in \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle[/math], то [math]A \setminus y_i \cup z_i \notin I[/math], то есть в [math]G_M(A)[/math] не существует ребра [math](y_i z_i)[/math]. Но тогда, как было отмечено ранее, не существует полного паросочетания. Получили противоречие. |
| [math]\triangleleft[/math] |
См. также
Источники информации