Триангуляция Делоне на сфере — различия между версиями
Dominica (обсуждение | вклад) (Новая страница: «== Определение == {{Определение |definition= '''Триангуляция''' — набор непересекающихся отрезков...») |
Dominica (обсуждение | вклад) м |
||
| Строка 16: | Строка 16: | ||
'''Триангуляция''' — разбиение геометрической фигуры на симплексы. | '''Триангуляция''' — разбиение геометрической фигуры на симплексы. | ||
}} | }} | ||
| + | ==Существования триангуляции Делоне== | ||
{{Лемма | {{Лемма | ||
|about=1 | |about=1 | ||
| Строка 21: | Строка 22: | ||
|proof= | |proof= | ||
[[Файл:drawing.png|400px|thumb|right|]] | [[Файл:drawing.png|400px|thumb|right|]] | ||
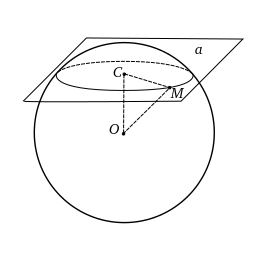
| + | Пусть плоскость <tex>\alpha</tex> пересекает сферу. Из центра <tex>O</tex> опустим перпендикуляр <tex>OC</tex> на плоскость <tex>\alpha</tex>. | ||
| + | Соединим произвольную точку <tex>M</tex> линии пересения плоскости <tex>\alpha</tex> со сферой с точками <tex>O</tex> и <tex>C</tex>. Так как <tex>OC</tex> ⊥ <tex>\alpha</tex>, то <tex>OC</tex> ⊥ <tex>CM</tex>. | ||
| + | |||
| + | В прямоугольном треугольнике <tex>OCM CM2 = OM2 - OC2</tex>. Т.к. <tex>OM</tex> и <tex>OC</tex> - величины постоянные, то и <tex>CM</tex> - величина постоянная. Таким образом все точки линии пересечения плоскости <tex>/alpha</tex> и сферы равноудалены от точки <tex>C</tex>, поэтому эта линия пересечения является окружностью с центром в точке <tex>C</tex> и радиусом <tex>r = CM</tex>. | ||
}} | }} | ||
Версия 06:15, 18 ноября 2016
Определение
| Определение: |
| Триангуляция — набор непересекающихся отрезков, соединениющий заданный набор точек так, что добавление новых отрезков невозможно без пересечения уже имеющихся. |
| Определение: |
| Отрезок — кратчайшее расстояние от точки до точки на заданной поверхности. |
| Определение: |
| Симплекс — геометрическая фигура, являющаяся n-мерным обобщением треугольника. |
| Определение: |
| Триангуляция — разбиение геометрической фигуры на симплексы. |
Существования триангуляции Делоне
| Лемма (1): |
Сечение сферы плоскостью есть круг, а основание перпендикуляра проведенного из центра шара к пересекаемой плоскости есть центр круга, полученного в сечении. |
| Доказательство: |
|
Пусть плоскость пересекает сферу. Из центра опустим перпендикуляр на плоскость . Соединим произвольную точку линии пересения плоскости со сферой с точками и . Так как ⊥ , то ⊥ . В прямоугольном треугольнике . Т.к. и - величины постоянные, то и - величина постоянная. Таким образом все точки линии пересечения плоскости и сферы равноудалены от точки , поэтому эта линия пересечения является окружностью с центром в точке и радиусом . |