Теорема Вагнера — различия между версиями
Ksushka (обсуждение | вклад) |
Ksushka (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
<b>Минором графа</b> (англ. ''Graph minor'') <tex>G</tex> будем называть граф <tex>H</tex>, если <tex>H</tex> может быть образован из <tex>G</tex> удалением рёбер и вершин или стягиванием рёбер. | <b>Минором графа</b> (англ. ''Graph minor'') <tex>G</tex> будем называть граф <tex>H</tex>, если <tex>H</tex> может быть образован из <tex>G</tex> удалением рёбер и вершин или стягиванием рёбер. | ||
}} | }} | ||
| + | |||
| + | |||
| + | |||
| + | == Пример == | ||
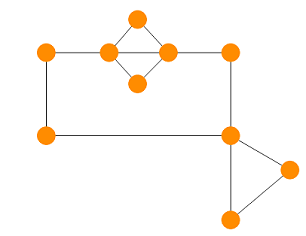
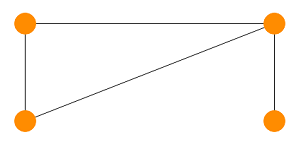
| + | В следующем примере граф <tex>H</tex> является минором графа <tex>G</tex>: | ||
| + | |||
| + | <tex>G</tex> [[Файл:Olddddd.png]] | ||
| + | |||
| + | <tex>H</tex>[[Файл:Olllddd.png]] | ||
Версия 18:34, 27 ноября 2016
Содержание
| Определение: |
| Минором графа (англ. Graph minor) будем называть граф , если может быть образован из удалением рёбер и вершин или стягиванием рёбер. |
Пример
В следующем примере граф является минором графа :
| Теорема: |
Граф планарен тогда и только тогда, когда его миноры не содержат ни ни . |
| Доказательство: |
|
Иначе говоря в соответствии с теоремой Понтрягина-Куратовского, теорему можно переформулировать: « В графе есть миноры содержащие или тогда и только тогда, когда существует подграф гомеоморфный или »
Разделим доказательство на две части
Доказательство первой части
В силу определения минора, если в существует минор содержащий ,значит существуют множества вершин , , , , , попарно не пересекающиеся, образующие индуцированный связанный подграф , такие что для каждого и существует и , такие что , принадлежит множеству ребер исходного графа. Следовательно для каждого существует поддерево в , у которого три листа , , , а все остальные вершины подграфа принадлежат . Ситуация с симметрична. Доказательство второй части
В силу определения минора, если в существует минор содержащий ,значит существуют множества вершин попарно не пересекающиеся, образующие индуцированный связанный подграф , такие что для всех существует и , такие что ( ) принадлежит множеству ребер исходного графа. Следовательно для любого существует поддерево в с четырьмя листьями, по одному листу в каждом и с остальными вершинами внутри .
Такое "обрезание" приведет к тому что будут иметь по три вершины, каждая содержится в таком подграфе, что она окрашено в другой цвет чем остальные вершины. Граф сформированный из красных и синих вершин вместе с оставшимися ребрами изоморфен .
|
См. также
Источники информации
- Graph minor — Wikipedia
- Geir Agnarsson, Raymond Greenlaw. Graph Theory: Modeling, Applications and Algorithms, 2006 — глава 7.5 стр. 210