Деревья Эйлерова обхода — различия между версиями
Sokolova (обсуждение | вклад) (→Euler Tours on Trees) |
Sokolova (обсуждение | вклад) (→Euler Tours on Trees) |
||
| Строка 17: | Строка 17: | ||
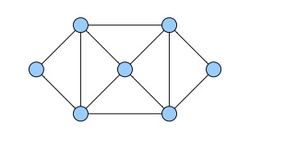
[[Файл:Simple graph.png |400px|thumb|center|Пример ]] | [[Файл:Simple graph.png |400px|thumb|center|Пример ]] | ||
| + | |||
| + | Euler Tours on Trees | ||
| + | |||
| + | In general, trees do not have Euler tours. | ||
| + | |||
| + | [[Файл:Simple graph.png |400px|thumb|center|Пример ]] | ||
| + | |||
| + | Technique: replace each edge {u, v} with two edges (u, v) and (v, u).<br> | ||
| + | Resulting graph has an Euler tour. | ||
| + | |||
| + | High-level idea: Instead of storing the trees in the forest, store their Euler tours. | ||
| + | Each edge insertion or deletion translates into a set of manipulations on the Euler tours of the trees in the forest.<br> | ||
| + | Checking whether two nodes are connected can be done by checking if they're in the same Euler tour. | ||
==Properties of Euler Tours== | ==Properties of Euler Tours== | ||
Версия 22:19, 28 ноября 2016
Содержание
Введение
Динамические деревья (англ.dynamic tree) используются в двух областях:.........
Нужно поддерживать следующие операции
- — добавить ребро (u, w) (при условии, что вершины u w принадлежат разным деревьям)
- — разрезать ребро (u, w) (при условии, что ребро (u, w) принадлежит дереву),
- — принадлежат ли вершины u и w одной компоненте связности.
Euler tour tree - The data structure we'll develop can perform these operations time O(log n) each.
Euler Tours on Trees
Euler Tours
In a graph G, an Euler tour is a path through the graph that visits every edge exactly once.
Mathematically formulates the “trace this figure without picking up your pencil or redrawing any lines” puzzles.
Euler Tours on Trees
In general, trees do not have Euler tours.
Technique: replace each edge {u, v} with two edges (u, v) and (v, u).
Resulting graph has an Euler tour.
High-level idea: Instead of storing the trees in the forest, store their Euler tours.
Each edge insertion or deletion translates into a set of manipulations on the Euler tours of the trees in the forest.
Checking whether two nodes are connected can be done by checking if they're in the same Euler tour.
Properties of Euler Tours
Операции
Rerooting a Tour
link(u ,v)
cut(u ,v)
Реализация структуры
Linked Lists
Balanced Trees
Сравнительная табличка
Похожие структуры
Про link-cut trees