Коды Грея для перестановок — различия между версиями
Niko (обсуждение | вклад) (→Построения Кода Грея для перестановок) |
Niko (обсуждение | вклад) (→Сведение задачи построение кода Грея для перестановок к графам) |
||
| Строка 62: | Строка 62: | ||
== '''Сведение задачи построение кода Грея для перестановок к графам''' == | == '''Сведение задачи построение кода Грея для перестановок к графам''' == | ||
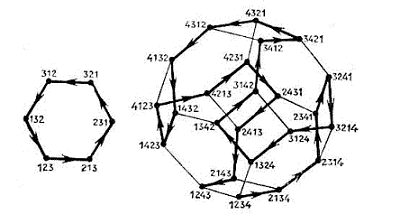
| − | Последовательность перестановок, полученная с помощью данного алгоритма имеет интересную интерпретацию. Так, если рассмотреть граф, вешины которого соответствуют всем перестановкам и в котором две вершины, соответствующие перестановкам f и g, соединены ребром, если g образуется из f однократной транспозицией соседних элементов, то полученная последовательность является гамильтоновым путем в этом графе. На рисунке изображен граф последовательности для n = 3, 4. | + | Последовательность перестановок, полученная с помощью данного алгоритма имеет интересную интерпретацию. Так, если рассмотреть граф, вешины которого соответствуют всем перестановкам и в котором две вершины, соответствующие перестановкам <tex>f</tex> и <tex>g</tex>, соединены ребром, если g образуется из f однократной транспозицией соседних элементов, то полученная последовательность является гамильтоновым путем в этом графе. На рисунке изображен граф последовательности для <tex>n</tex> = 3, 4. |
[[Изображение:Pic4.gif]] | [[Изображение:Pic4.gif]] | ||
| + | |||
== См. также == | == См. также == | ||
* [[Коды Грея]] | * [[Коды Грея]] | ||
* [[Комбинаторные объекты]] | * [[Комбинаторные объекты]] | ||
* [[Гамильтонов путь]] | * [[Гамильтонов путь]] | ||
Версия 22:50, 9 декабря 2010
код Грея для перестановки при n = 2
1 2 2 1 |
код Грея для перестановки при n = 3
1 2 3 2 1 3 2 3 1 3 2 1 3 1 2 1 3 2 |
код Грея для перестановки при n = 4
1 2 3 4 2 1 3 4 2 3 1 4 2 3 4 1 3 2 4 1 3 2 1 4 3 1 2 4 1 3 2 4 1 3 4 2 3 1 4 2 3 4 1 2 3 4 2 1 4 3 2 1 4 3 1 2 4 1 3 2 1 4 3 2 1 4 2 3 4 1 2 3 4 2 1 3 4 2 3 1 2 4 3 1 2 4 1 3 2 1 4 3 1 2 4 3 |
Содержание
Определение
Коды Грея для перестановок - называют такое упорядочение перестановок, что соседние перестановки отличаются только элементарной транспозицией.
Построения Кода Грея для перестановок
Строим из рекурсивных соображений. При фиксированной перестановки из элемента можно перебрать все вариантов добавления к этой перестановке элемента , и этот перебор можно осуществить передвигая элемент каждый раз на соседнее место, Например
3652147 -> 3652174 -> 3652714 -> 3657214 и т. д.
На фоне перебора позиций -го элемента должны проводиться переборы перестановок меньшего порядка, к которым применяется тот же принцип, т.е., например в нашем случае после получения набора 7365214 требуется сдвинуть влево или вправо элемент 6.
Действовать будем так. Каждые итерации будем давать команду на сдвиг -го элемента, а затем менять направление движения его на противоположное и будем давать команду на сдвиг элемента с меньшим номером; для этих выделенных итераций нужно делать то же самое: на из них двигать -й элемент, а на -й итерации сменить ему направление движения, и т.д.
Построение. Кроме рабочей перестановки и её номера в факториальной системе (младший разряд - последний) потребуется иметь массив , задающий текущее направления движения всех элементов. Удобно еще иметь массив, сопоставляющий каждому элементу то место , на котором стоит стоит в перестановке .
Начальное состояние.
Сведение задачи построение кода Грея для перестановок к графам
Последовательность перестановок, полученная с помощью данного алгоритма имеет интересную интерпретацию. Так, если рассмотреть граф, вешины которого соответствуют всем перестановкам и в котором две вершины, соответствующие перестановкам и , соединены ребром, если g образуется из f однократной транспозицией соседних элементов, то полученная последовательность является гамильтоновым путем в этом графе. На рисунке изображен граф последовательности для = 3, 4.