Регулярная аппроксимация КС-языков

Определения

Определение:

Контекстно-свободная грамматика [math] G = \langle N, \Sigma, P, S \rangle[/math] называется самоприменимой (англ. self-embeded), если [math] \exists A \in N: A \Rightarrow^* \alpha A \beta[/math], [math] \alpha \neq \varepsilon \land \beta \neq \varepsilon [/math] .

Определение:

Нетерминал [math] A \in N[/math] в грамматике [math] G = \langle N, \Sigma, P, S \rangle[/math] называется рекурсивным (англ. recursive), если [math] \exists \alpha,\beta \in (\Sigma \cup N)^* : A \Rightarrow^* \alpha A \beta[/math] .

Определение:

Нетерминалы [math] A,B \in N[/math] в грамматике [math] G = \langle N, \Sigma, P, S \rangle[/math] называются взаимно рекурсивными (англ. mutual recursive), если [math] \exists \alpha_1,\beta_1,\alpha_2,\beta_2 \in (\Sigma \cup N)^* : A \Rightarrow^* \alpha_1 B \beta_1 \land B \Rightarrow^* \alpha_2 A \beta_2[/math] .

Алгоритм преобразования грамматики в конечный автомат

Лемма:

Не самоприменимая контекстно-свободная грамматика генерирует регулярный язык.

Доказательство:

[math]\triangleright[/math]

В качестве конструктивного доказательства, мы приведем алгоритм построения конечного автомата по грамматике. Для желающих, приведем ссылку на формальное доказательство.

[math]\triangleleft[/math]

Идея алгоритма

Пусть, [math] N^* [/math] множество рекурсивных терминалов из [math] N [/math]. Пусть, [math] P = \{N_1,N_2,...,N_K\} [/math] разбиение [math] N^*[/math] на [math] k [/math] дизъюнктных множеств взаимно рекурсивных терминалов, [math] N_1 \cup N_2 \cup ... \cup N_k = N^* \land \forall i N_i \neq \emptyset [/math].

function IsLeftType([math]N_i[/math])
    return [math] \exists (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \alpha \neq \varepsilon ][/math]

function IsRightType([math]N_i[/math])
    return [math] \exists (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \beta \neq \varepsilon ][/math]

Введем функцию [math] getTheTypeOfMutualRecursiveSet(N_i): P \rightarrow \{left, right, self, cycle\} [/math]:

function getTheTypeOfMutualRecursiveSet ([math]N_i[/math]):
   if !IsLeftType([math]N_i[/math]) && IsRightType([math]N_i[/math]) 
       return left;
   if IsLeftType([math]N_i[/math]) && !IsRightType([math]N_i[/math]) 
       return right;
   if (IsLeftType([math]N_i[/math]) && IsRightType([math]N_i[/math]) 
       return self;
   if !IsLeftType([math]N_i[/math]) && !IsRightType([math]N_i[/math]) 
       return cyclic;

Заметим, что [math] \forall i [/math] [math]getTheTypeOfMutualRecursiveSet(N_i) \neq self [/math], т.к в противном случае грамматика будет самоприменима.
В основе алгоритма будет рекурсивный обход грамматики. Спускаемся по грамматике до тех пор не приходим в нетерминал или символ алфавита:

1. символ алфавит или [math] \varepsilon [/math] — добавляем новое правило в автомат
2. нерекурсивный нетерминал — запускаемся от всех правых частей правил, который терминал порождает
3. рекурсивный нетерминал — в зависимости от типа рекурсивного нетерминала, продолжаем рекурсию (будет ясно из пседокода)

Псевдокод

[math]Q[/math] — множество состояний ДКА.

[math]\Delta[/math] — множество переходов ДКА.

[math]T[/math] — множество допускающих состояний.

function createFA(G)               // [math] G = \langle N, \Sigma, P, S \rangle[/math] 
    [math]\mathtt{Q} \leftarrow \varnothing[/math]
    [math]\Delta \leftarrow \varnothing [/math]
    s = createState
    f = createState
    [math]F \leftarrow \{f\} [/math]
    return makeFA (s,S,f)
     
function makeFA (q0,a,q1)
   if a == [math] \varepsilon [/math] || a [math] \in \Sigma[/math]             // пришли в лист дерева разбора
        [math] \Delta = \Delta \cup \{(q_0,a,q_1)\} [/math]
        return
   if a == [math]X\beta[/math] where [math] X \in (N \cup \Sigma) \land \beta \in (N \cup \Sigma)^* \land |\beta| \gt  0 [/math]  
        q = createState
        makeFA ([math]q_0,X,q_1[/math])
        makeFA ([math]q, \beta, q_1 [/math])
        return
    if exist [math] N_i [/math] where [math] a \in N_i [/math]  
         foreach b in [math]N_i[/math] 
            [math]q_b[/math] = createState
         if getTheTypeOfMutualRecursiveSet([math] N_i [/math]) == left 
            foreach C in [math]N_i[/math] where [math] C \rightarrow X_1...X_m \land X_1,...X_m \neq N_i [/math]
               makeFA ([math]q_0, X_1 \cdots X_m, q_C[/math])             
            foreach C,D in [math]N_i[/math] where [math] C \rightarrow DX_1...X_m \land X_1,...X_m \neq N_i [/math]
               makeFA ([math]q_D, X_1 \cdots X_m, q_C[/math])
               [math] \Delta = \Delta \cup \{(q_a,\varepsilon,q_1)\} [/math]
          else                      // рекурсивный нетерминал right или cyclic   
            foreach C in [math]N_i[/math] where [math] C \rightarrow X_1...X_m \land X_1,...X_m \neq N_i [/math]
               makeFA ([math]q_C, X_1 \cdots X_m, q_1[/math])             
            foreach C,D in [math]N_i[/math] where [math] C \rightarrow DX_1...X_m \land X_1,...X_m \neq N_i [/math]
               makeFA ([math]q_D, X_1 \cdots X_m, q_C[/math])
               [math] \Delta = \Delta \cup \{(q_0, \varepsilon ,q_a)\} [/math] 
             return
    foreach p in [math]P[/math] where p == [math] a \rightarrow \beta [/math]
       makeFA ([math] q_0, \beta, q_1 [/math])

Аппроксимации самоприменимой грамматики

В данном разделе покажем методы апроксимации: RTN (recursive transition network) аппроксимацию и MN (Mohri and Nederhof's) аппроксимацию — самоприменимой контекстно-свободной грамматики [math] G = \langle N, \Sigma, P, S \rangle[/math] к регулярной грамматике. Для удобства будем считать, что грамматика представлена в НФХ.

Автоматы [math]T_A,T_B[/math] для грамматики [math]A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f [/math]

RTN аппроксимация

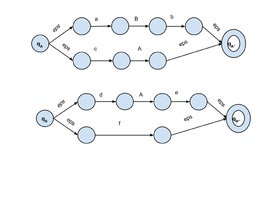
Построим, по данной грамматике аппроксимирующий ее конечный автомат.

Конечный автомат для грамматики [math]A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f [/math]

1. Для каждого нетерминала [math] A[/math] в грамматике, создадим новый конечный автомат [math] T_A[/math], добавим в него два состояния [math] q_A[/math] и [math]q_{A^*}[/math].
2. Для каждого правила грамматике [math] (A \rightarrow X_1 \cdots X_m ) \in P[/math], введм новые состояния в автомат этого нетерминала [math] q_0^A \cdots q_m^A[/math], а также добавим новые правила перехода в [math] \Delta[/math]: [math] (q_A, \varepsilon, q_0),(q_0^A,X_1,q_1^A), \cdots,(q_{m-1}^A,X_m,q_m^A),(q_m^A,\varepsilon,q_{A^*})[/math].
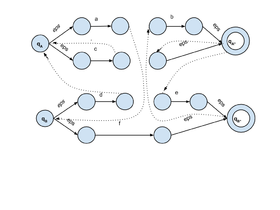
3. Таким образом мы построили множество конечных автоматов [math]T[/math] = [math] \{ T_A \| A \in N\}[/math] для каждого нетерминала [math]A[/math]. Теперь объединим все в один автомат. Объединим все состоянии автоматов из [math]T[/math] в множество [math]Q[/math]. Скопируем все переходы каждого автомата из [math]T[/math] в [math]\Delta[/math]. Далее для каждого перехода вида [math](q,A,p), A\in N[/math], вместо него добавим два новых перехода: [math] (q, \varepsilon, q_A),(q_A^{*}, \varepsilon, p) [/math].

MN аппроксимация

Построим по данной самоприменимой контекстно-свободной грамматике [math] G [/math] регулярную грамматику [math] G^*[/math].

1. Для каждого нетерминала [math] A \in N [/math] из [math]G[/math], добавим нетерминалы [math]A[/math] и [math] A^*[/math] в [math] G^* [/math].
2. Для каждого правила [math] A \rightarrow {\alpha}_{0} B_1 {\alpha}_{1} B_2 {\alpha}_{2} \cdots B_m {\alpha}_{m}[/math], где [math] B_1, \cdots, B_m \in N \land {\alpha}_i \in \Sigma^*[/math]. Добавим в [math] G^*[/math] нетерминалы [math] B_1 \cdots B_m , B_1^* \cdots B_m^*[/math] и следуюшие правила: [math] A \rightarrow {\alpha}_0 B_1 \\ B_1^* \rightarrow {\alpha}_1 B_2\\ \vdots \\ B^*_m \rightarrow {\alpha}_m A^* [/math].
   (Если [math]m = 0 [/math], тогда добавим правило [math] A \rightarrow {\alpha}_0 A^* [/math]).

В итоге [math] G^*[/math] — правоконтекстная грамматика, эквивалентная конечному автомату, который задает регулярный язык.

Пример

[math] G = \left\{\begin{matrix} A \rightarrow \alpha B \alpha \\ B \rightarrow \beta A | \beta \end{matrix}\right.\Rightarrow G^* = \left\{\begin{matrix} A \rightarrow \alpha B \\ A^* \rightarrow B^* | \varepsilon \\ B \rightarrow \beta A | \beta B^* \\ B^* \rightarrow \alpha A^* | \varepsilon \end{matrix}\right.[/math]
Исходная грамматика [math] G [/math] генерирует язык: [math] \{(ab)^n a^n | n \gt 0\}[/math]. Результирущая грамматика [math] G^*[/math] генирирует регулярный язык: [math] (ab)^+ a^*[/math].

Сравнение двух методов

Ясно, что оба языка, генерируемых конечным автомат для первого метода и апрокисимируещей граматикой для второго метода, содержат в себе язык генерируемый исходной грамматикой.
Привлекателным свойством MN аппроксимации по сравнению с RTN, то, что она можеть быть применима к большим грамматикам: для каждого нетерминала грамматике [math] G[/math], добавляется не более одного нового нетерминала в [math] G^*[/math] и размер результирующий грамматики максимум в [math]2[/math] раза больше, чем размер исходной. Так как для RTN апроксимации грамматики [math] G = \langle N, \Sigma, P, S \rangle[/math], количество состаяний апроксимируещего автомата в худшем случаи может составлять [math] O(|N|^2)[/math], что может быть критично для аппроксимации больших грамматик.
Также,еще несколько эффекивных методов аппрокимации можно найти в статьях, приведенных в ссылках.

Источники информации

• Jean-Claude Junqua,Gertjan van Noord — Robustness in Language and Speech Technology — Kluwer Academic Publishers, 2001 — ISBN 0-7923-6790-1
• Strongly Regular Grammars and Regular Approximation of Contex-Free Languages
• Willem J. M. Levelt — An Introduction to the Theory of Formal Languages and Automata — John Benjamin B.V., 2008 — ISBN 978-90-272-3250-2