Алгоритм Эдмондса-Карпа — различия между версиями
Shersh (обсуждение | вклад) м (→Пример графа на котором алгоритм дает плохую асимптотику) |
(ребра -> рёбра) |
||
| Строка 1: | Строка 1: | ||
== Алгоритм == | == Алгоритм == | ||
| − | Алгоритм Эдмондса-Карпа является реализацией метода [[Алгоритм Форда-Фалкерсона для поиска максимального паросочетания|Форда-Фалкерсона]], в которой в качестве дополняющего пути выбирается [[Обход в ширину |кратчайший по | + | Алгоритм Эдмондса-Карпа является реализацией метода [[Алгоритм Форда-Фалкерсона для поиска максимального паросочетания|Форда-Фалкерсона]], в которой в качестве дополняющего пути выбирается [[Обход в ширину |кратчайший по рёбрам путь]] в остаточной сети (длины всех рёбер равны <tex>1</tex>). |
=== Описание === | === Описание === | ||
| Строка 54: | Строка 54: | ||
|statement=Пусть для некоторой сети <tex>G(V,E)</tex> с источником <tex>s</tex> и стоком <tex>t</tex> выполняется алгоритм Эдмондса-Карпа, тогда общее число итераций цикла <tex>\mathrm {while}</tex> составляет <tex>O(V E)</tex>. | |statement=Пусть для некоторой сети <tex>G(V,E)</tex> с источником <tex>s</tex> и стоком <tex>t</tex> выполняется алгоритм Эдмондса-Карпа, тогда общее число итераций цикла <tex>\mathrm {while}</tex> составляет <tex>O(V E)</tex>. | ||
|proof= | |proof= | ||
| − | Рассмотрим множество | + | Рассмотрим множество рёбер <tex>(u,v)</tex> остаточной сети <tex>G_f</tex>, принадлежащих увеличивающему пути <tex>p</tex>, таких что <tex>c_f(p) = c_f(u,v)</tex>. Назовем данные рёбра критическими. Покажем, что каждое из <tex>|E|</tex> рёбер может становиться критическим не более, чем <tex>|V| - 1</tex> раз. Заметим, что после увеличения потока вдоль пути <tex>p</tex> все критические рёбра исчезают из остаточной сети, кроме того по определению остаточной пропускной способности пути хотя бы одно ребро увеличивающего пути {{---}} критическое. |
| − | Рассмотрим две вершины <tex>u</tex> и <tex>v</tex> принадлежащие <tex>V</tex>, соединенные некоторым ребром из <tex>E</tex>. Увеличение производится вдоль кратчайших путей, поэтому если ребро <tex>(u,v)</tex> становиться критическим в первый раз, верно, что <tex>\delta_f(s,v) = \delta_f(s,u) + 1</tex>. После увеличения потока ребро <tex>(u, v)</tex> исчезает из сети. Оно не появится в другом увеличивающем пути до тех, пор пока не будет | + | Рассмотрим две вершины <tex>u</tex> и <tex>v</tex> принадлежащие <tex>V</tex>, соединенные некоторым ребром из <tex>E</tex>. Увеличение производится вдоль кратчайших путей, поэтому если ребро <tex>(u,v)</tex> становиться критическим в первый раз, верно, что <tex>\delta_f(s,v) = \delta_f(s,u) + 1</tex>. После увеличения потока ребро <tex>(u, v)</tex> исчезает из сети. Оно не появится в другом увеличивающем пути до тех, пор пока не будет уменьшено по обратному ребру <tex>(v, u)</tex>. Это может произойти только в том случае, если ребро <tex>(v, u)</tex> встретится на некотором увеличивающем пути. Пусть в момент перед увеличением поток в сети <tex>G</tex> составлял <tex>f'</tex>, то поскольку увеличение производиться вдоль кратчайших путей, верно: <tex>\delta'_f(s,u) = \delta'_f(s, v) + 1</tex>. Согласно [[#lemma1|лемме]] <tex>\delta_f(s,v) \leqslant \delta'_f(s,v)</tex>, откуда <tex>\delta'_f(s,u) = \delta'(s,v) + 1 \geqslant \delta_f(s,v) + 1 = \delta_f(s,u) + 2</tex>. |
| − | Итак в промежуток времени между тем, когда ребро <tex>(u,v)</tex> становится критическим в первый раз, до момента, когда оно становится критическим в следующий раз, расстояние от <tex>s</tex> до <tex>u</tex> увеличивается минимум на <tex>2</tex>. Расстояние <tex>\delta(s,u)</tex> в начальный момент времени больше либо равно <tex>0</tex>. Среди промежуточных вершин на кратчайшем пути <tex>s \leadsto u</tex> не могут находиться <tex>s</tex>, <tex>u</tex> или <tex>t</tex>. Следовательно к тому моменту, когда вершина <tex>u</tex> станет недостижимой из источника расстояние до нее не превысит <tex>|V| - 2</tex>. Получаем, что ребро <tex>(u, v)</tex> могло стать критическим не более <tex>\dfrac{(|V| -2)}{2} = \dfrac{|V|}{2} - 1</tex> раз. Поскольку в графе не более <tex>O(E)</tex> пар вершин, между которыми могут существовать | + | Итак в промежуток времени между тем, когда ребро <tex>(u,v)</tex> становится критическим в первый раз, до момента, когда оно становится критическим в следующий раз, расстояние от <tex>s</tex> до <tex>u</tex> увеличивается минимум на <tex>2</tex>. Расстояние <tex>\delta(s,u)</tex> в начальный момент времени больше либо равно <tex>0</tex>. Среди промежуточных вершин на кратчайшем пути <tex>s \leadsto u</tex> не могут находиться <tex>s</tex>, <tex>u</tex> или <tex>t</tex>. Следовательно к тому моменту, когда вершина <tex>u</tex> станет недостижимой из источника расстояние до нее не превысит <tex>|V| - 2</tex>. Получаем, что ребро <tex>(u, v)</tex> могло стать критическим не более <tex>\dfrac{(|V| -2)}{2} = \dfrac{|V|}{2} - 1</tex> раз. Поскольку в графе не более <tex>O(E)</tex> пар вершин, между которыми могут существовать рёбра в остаточной сети, то общее количество критических рёбер в ходе выполнения алгоритма Эдмондса-Карпа равно <tex>O(V E)</tex>. |
Так как каждый увеличивающий путь содержит по крайней мере одно критическое ребро, следовательно число кратчайших путей составляет <tex>O(V E)</tex>. На каждой итерации цикла <tex>\mathrm {while}</tex> рассматривается ровно один увеличивающий путь, а поскольку в случае отсутствия такого пути выполнение цикла прерывается, то число итераций цикла <tex>\mathrm {while}</tex> также составляет <tex>O(V E)</tex>. | Так как каждый увеличивающий путь содержит по крайней мере одно критическое ребро, следовательно число кратчайших путей составляет <tex>O(V E)</tex>. На каждой итерации цикла <tex>\mathrm {while}</tex> рассматривается ровно один увеличивающий путь, а поскольку в случае отсутствия такого пути выполнение цикла прерывается, то число итераций цикла <tex>\mathrm {while}</tex> также составляет <tex>O(V E)</tex>. | ||
| Строка 68: | Строка 68: | ||
[[Файл:MaxFlowWorstCase.png|365px|thumb|right|«Грибок». Схема построения "сложного" для алгоритма Эдмондса-Карпа графа]] | [[Файл:MaxFlowWorstCase.png|365px|thumb|right|«Грибок». Схема построения "сложного" для алгоритма Эдмондса-Карпа графа]] | ||
| − | Заметим также, что | + | Заметим также, что существует ''сеть грибок''<ref>[https://www.topcoder.com/community/data-science/data-science-tutorials/maximum-flow-augmenting-path-algorithms-comparison/#! Cтатья на TopCoder.com ]</ref> на которой нижняя граница времени работы алгоритмы Эдмондса-Карпа также составляет <tex>\Omega(V E^2)</tex>. Рассмотрим этот случай более подробно. Норман Заде (англ. ''Norman Zadeh'') описал примеры, которые позволяют добиться асимптотики <tex>\Omega(V^3)</tex><ref>Norman Zadeh. Theoretical Efficiency of the Edmonds-Karp Algorithm for Computing Maximal Flows.</ref>. В нашем примере алгоритм выполнит <tex>\Omega(V^3)</tex> улучшений пути вне зависимости от выбора этого пути. |
Разделим все вершины (за исключением <tex>s</tex> и <tex>t</tex>) на подмножества: | Разделим все вершины (за исключением <tex>s</tex> и <tex>t</tex>) на подмножества: | ||
| − | *<tex>S={s_1,\ldots,s_k}</tex> — множество вершин, в которые входят | + | *<tex>S={s_1,\ldots,s_k}</tex> — множество вершин, в которые входят рёбра из <tex>s</tex> с пропускной способностью <tex>k</tex>, |
| − | *<tex>T={t_1,\ldots,t_k}</tex> — множество вершин, из которых исходят | + | *<tex>T={t_1,\ldots,t_k}</tex> — множество вершин, из которых исходят рёбра в <tex>t</tex> с пропускной способностью <tex>k</tex>, |
| − | *<tex>U={u_1,\ldots,u_{2p}}</tex> — множество вершин, достижимых из <tex>s</tex> по | + | *<tex>U={u_1,\ldots,u_{2p}}</tex> — множество вершин, достижимых из <tex>s</tex> по рёбрам с бесконечной пропускной способностью (не используя иные рёбра), |
| − | *<tex>V={v_1,\ldots,v_{2p}}</tex> — множество вершин, из которых можно достигнуть <tex>t</tex> по | + | *<tex>V={v_1,\ldots,v_{2p}}</tex> — множество вершин, из которых можно достигнуть <tex>t</tex> по рёбрам с бесконечной пропускной способностью (не используя иные рёбра). |
| − | <tex>S</tex> и <tex>T</tex> содержат <tex>k</tex> вершин, <tex>U</tex> и <tex>V</tex> содержат <tex>2p</tex> вершин. Где <tex>k</tex> и <tex>p</tex> фиксированные целые числа. Каждое ребро, выделенное жирным(см. рисунок, соединяют множества <tex>S</tex> и <tex>T</tex>), имеет единичную пропускную способность; пунктирные | + | <tex>S</tex> и <tex>T</tex> содержат <tex>k</tex> вершин, <tex>U</tex> и <tex>V</tex> содержат <tex>2p</tex> вершин. Где <tex>k</tex> и <tex>p</tex> фиксированные целые числа. Каждое ребро, выделенное жирным(см. рисунок, соединяют множества <tex>S</tex> и <tex>T</tex>), имеет единичную пропускную способность; пунктирные рёбра имеют бесконечную пропускную способность; остальные рёбра(в форме дуги) имеют пропускную способность <tex>k</tex>. |
| − | В начале работы алгоритма путь увеличиться <tex>k^2</tex> раз по пути (<tex>s</tex>, <tex>S</tex>, <tex>T</tex>, <tex>t</tex>), длина которого равна трем. После этого остаточная сеть будет содержать обратные | + | В начале работы алгоритма путь увеличиться <tex>k^2</tex> раз по пути (<tex>s</tex>, <tex>S</tex>, <tex>T</tex>, <tex>t</tex>), длина которого равна трем. После этого остаточная сеть будет содержать обратные рёбра из <tex>T</tex> в <tex>S</tex>, и алгоритм выберет еще <tex>k^2</tex> путей <tex>(s, u_1, u_2, T, S, v_2, v_1, t)</tex> длины <tex>7</tex>, затем путь <tex>(s, u_1, u_2, u_3, u_4, S, T, v_4, v_3, v_2, v_1, t)</tex> длины <tex>11</tex> и так далее. |
:Число вершин в сети: <tex>n = 2\cdot k + 4\cdot p + 2</tex>. | :Число вершин в сети: <tex>n = 2\cdot k + 4\cdot p + 2</tex>. | ||
| − | :Число | + | :Число рёбер: <tex> m = k^2 + 2\cdot p\cdot k + 2\cdot k + 4\cdot p</tex>. |
Нетрудно заметить, что число удлиняющих путей <tex> a = k^2\cdot (p+1)</tex>. | Нетрудно заметить, что число удлиняющих путей <tex> a = k^2\cdot (p+1)</tex>. | ||
| Строка 84: | Строка 84: | ||
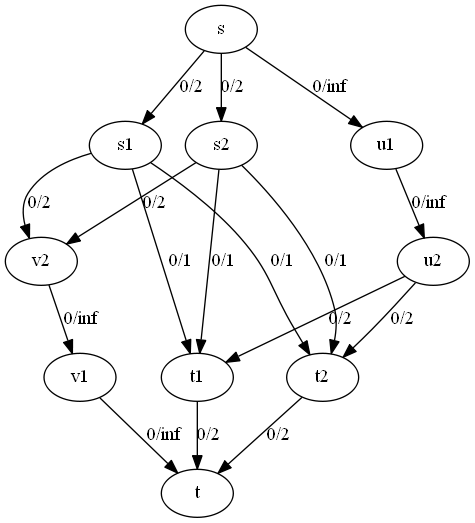
[[Файл:InGraph.png|600px|thumb|left| Изначальный граф, нулевой поток]] | [[Файл:InGraph.png|600px|thumb|left| Изначальный граф, нулевой поток]] | ||
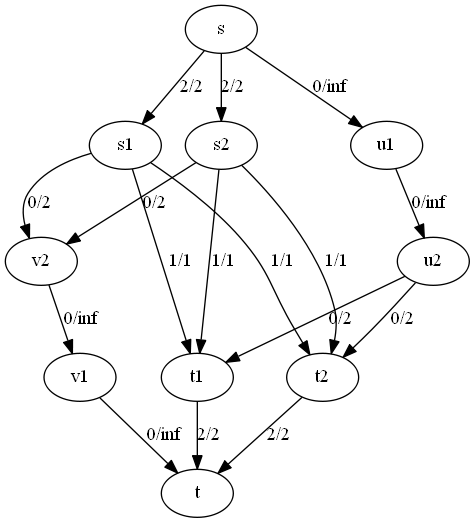
| − | [[Файл:SecondStage.png|600px|center|thumb| Граф после <tex>k^2</tex> поисков пути(в нашем случае <tex>k^2 = 4</tex>).<br/> | + | [[Файл:SecondStage.png|600px|center|thumb| Граф после <tex>k^2</tex> поисков пути(в нашем случае <tex>k^2 = 4</tex>).<br/>Рёбра из между множествами <tex>S</tex> и <tex>T</tex> полностью насыщены. Поток равен четырем]] |
| − | [[Файл:ThirdStageEdmunds karp.png|600px|thumb|left| Алгоритм нашел путь через | + | [[Файл:ThirdStageEdmunds karp.png|600px|thumb|left| Алгоритм нашел путь через рёбра бесконечной вместимости, совершив еще <tex>k^2 = 4</tex> шагов. Поток равен восьми]] |
==Примечания== | ==Примечания== | ||
Версия 14:14, 21 января 2017
Содержание
Алгоритм
Алгоритм Эдмондса-Карпа является реализацией метода Форда-Фалкерсона, в которой в качестве дополняющего пути выбирается кратчайший по рёбрам путь в остаточной сети (длины всех рёбер равны ).
Описание
- Положим все потоки равными нулю. Остаточная сеть изначально совпадает с исходной сетью.
- В остаточной сети находим кратчайший путь из источника в сток. Если такого пути нет, останавливаемся.
- Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:
- На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью .
- Для каждого ребра на найденном пути увеличиваем поток на , а в противоположном ему — уменьшаем на .
- Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.
- Возвращаемся на шаг 2.
Сложность
Сложность алгоритма Эдмондса-Карпа равна .
Псевдокод
function EdmondsKarp(G, s, t):
for (для) каждого ребра
while существует кратчайший путь из в в остаточной сети
for
Корректность алгоритма Эдмондса-Карпа
На каждой итерации цикла поток в графе увеличивается вдоль одного из кратчайших путей в из истока в сток . Этот процесс повторяется до тех пор пока существует кратчайший путь в . Если в не существует кратчайшего пути из в , значит, не существует никакого вообще никакого пути в следовательно по теореме Форда-Фалкерсона найденный поток максимальный.
Оценка быстродействия
| Лемма: |
Если в сети с истоком и стоком увеличение потока производится вдоль кратчайших путей в , то для всех вершин длина кратчайшего пути в остаточной сети не убывает после каждого увеличения потока. |
| Доказательство: |
|
Предположим противное, пусть существует вершина , что после какого-то увеличения потока длина кратчайшего пути из в уменьшилась. Обозначим потоки до и после увеличения соответственно за и . Пусть — вершина, расстояние от до которой минимально и уменьшилось с увеличением потока. Имеем . Рассмотрим путь , являющийся кратчайшим от к в . Тогда верно, что . По выбору и из предыдущего утверждения получаем, что . Предположим , тогда . Это противоречит . Пусть , но известно, что . Появление ребра после увеличения потока означает увеличение потока по обратному ребру . Увеличение потока производится вдоль кратчайшего пути, поэтому кратчайший путь из в вдоль которого происходило увеличения выглядит как , из чего получаем . Данное утверждение противоречит . Итак мы пришли к противоречию с существованием вершины , кратчайшее расстояние до которой уменьшилось с увеличением потока. |
Опираясь на предшествующую лемму, докажем следующую теорему, которая ограничивает сверху число итераций цикла в алгоритме Эдмондса-Карпа.
| Теорема: |
Пусть для некоторой сети с источником и стоком выполняется алгоритм Эдмондса-Карпа, тогда общее число итераций цикла составляет . |
| Доказательство: |
|
Рассмотрим множество рёбер остаточной сети , принадлежащих увеличивающему пути , таких что . Назовем данные рёбра критическими. Покажем, что каждое из рёбер может становиться критическим не более, чем раз. Заметим, что после увеличения потока вдоль пути все критические рёбра исчезают из остаточной сети, кроме того по определению остаточной пропускной способности пути хотя бы одно ребро увеличивающего пути — критическое. Рассмотрим две вершины и принадлежащие , соединенные некоторым ребром из . Увеличение производится вдоль кратчайших путей, поэтому если ребро становиться критическим в первый раз, верно, что . После увеличения потока ребро исчезает из сети. Оно не появится в другом увеличивающем пути до тех, пор пока не будет уменьшено по обратному ребру . Это может произойти только в том случае, если ребро встретится на некотором увеличивающем пути. Пусть в момент перед увеличением поток в сети составлял , то поскольку увеличение производиться вдоль кратчайших путей, верно: . Согласно лемме , откуда . Итак в промежуток времени между тем, когда ребро становится критическим в первый раз, до момента, когда оно становится критическим в следующий раз, расстояние от до увеличивается минимум на . Расстояние в начальный момент времени больше либо равно . Среди промежуточных вершин на кратчайшем пути не могут находиться , или . Следовательно к тому моменту, когда вершина станет недостижимой из источника расстояние до нее не превысит . Получаем, что ребро могло стать критическим не более раз. Поскольку в графе не более пар вершин, между которыми могут существовать рёбра в остаточной сети, то общее количество критических рёбер в ходе выполнения алгоритма Эдмондса-Карпа равно . Так как каждый увеличивающий путь содержит по крайней мере одно критическое ребро, следовательно число кратчайших путей составляет . На каждой итерации цикла рассматривается ровно один увеличивающий путь, а поскольку в случае отсутствия такого пути выполнение цикла прерывается, то число итераций цикла также составляет . |
Если увеличивающий путь находить поиском в ширину, то каждую итерацию цикла можно выполнить за время . Инициализация в процедуре Edmonds Karp производится за , следовательно время работы алгоритма алгоритма Эдмондса-Карпа составляет .
Пример графа на котором алгоритм дает плохую асимптотику
Заметим также, что существует сеть грибок[1] на которой нижняя граница времени работы алгоритмы Эдмондса-Карпа также составляет . Рассмотрим этот случай более подробно. Норман Заде (англ. Norman Zadeh) описал примеры, которые позволяют добиться асимптотики [2]. В нашем примере алгоритм выполнит улучшений пути вне зависимости от выбора этого пути. Разделим все вершины (за исключением и ) на подмножества:
- — множество вершин, в которые входят рёбра из с пропускной способностью ,
- — множество вершин, из которых исходят рёбра в с пропускной способностью ,
- — множество вершин, достижимых из по рёбрам с бесконечной пропускной способностью (не используя иные рёбра),
- — множество вершин, из которых можно достигнуть по рёбрам с бесконечной пропускной способностью (не используя иные рёбра).
и содержат вершин, и содержат вершин. Где и фиксированные целые числа. Каждое ребро, выделенное жирным(см. рисунок, соединяют множества и ), имеет единичную пропускную способность; пунктирные рёбра имеют бесконечную пропускную способность; остальные рёбра(в форме дуги) имеют пропускную способность . В начале работы алгоритма путь увеличиться раз по пути (, , , ), длина которого равна трем. После этого остаточная сеть будет содержать обратные рёбра из в , и алгоритм выберет еще путей длины , затем путь длины и так далее.
- Число вершин в сети: .
- Число рёбер: .
Нетрудно заметить, что число удлиняющих путей . Возьмем равным . В этом случае и . Заде приводит более хитрые примеры с такой же асимптотикой, но они зависят от выбора пути.
Примечания
- ↑ Cтатья на TopCoder.com
- ↑ Norman Zadeh. Theoretical Efficiency of the Edmonds-Karp Algorithm for Computing Maximal Flows.
Источники информации
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
- Википедия: Алоритм Эдмондса-Карпа
- Википедия: Алоритм Эдмондса-Карпа (англ.)
- Статья на TopCoder.com