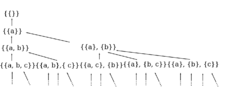Числа Белла

Определение:

В комбинаторной математике числа Белла(англ. Bell's numbers) показывают количество возможных способов разбиения множества из n элементов на непустые подмножества.

Числа Белла начинаются с [math]B_0=B_1=1[/math] и образуют последовательность :

1, 1,2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437, 190899322, 1382958545, 10480142147, 82864869804, 682076806159, 5832742205057, ...

[math]n[/math]- элемент чисел Белла, [math]B_n[/math], показывает количество различных способов разбиения множества, то есть. количество отношений эквивалентности в нем. Вне математики, похожие числа показывают количество различных схем рифмовки для [math]n[/math]-й строфы стихотворения. Эти числа изучались математиками с 17-го века, их корни уходят в средневековую Японию. Названы в честь Эрика Темпла Белла, который описал их в 1930-х годах.

Подсчет

Разделение набора

Разбиения множеств могут быть расположены частично-упорядоченном виде. Каждое подмножество длины n использует одно из подмножеств длины[math]n-1[/math].

52 разбиения множества из 5 элементов

[math]B_n[/math] количество разбиений множества размера [math]n[/math]. Разбиение множества [math]S[/math] определяется как совокупность 'непустых, попарно непересекающихся подмножеств множества' [math]S[/math]. Например, B₃ = 5, потому что множество, состоящее их 3 элементов {a, b, c} может быть разделено 5 различным способами:

{ {a}, {b}, {c} }

{ {a}, {b, c} }

{ {b}, {a, c} }

{ {c}, {a, b} }

{ {a, b, c} }.

[math]B_0[/math] является 1, т.к. существует только одно возможное разбиение пустого множества. Каждый элемент пустого множества является непустым множеством и их объединение является пустым множеством. Таким образом, пустое множество может разбиваться только на само себя. Как было обозначено выше, мы не рассматриваем ни порядок подмножеств, ни порядок элементов в каждом их них . Это означает, что данные разбиения являются идентичными:

{ {b}, {a, c} }

{ {a, c}, {b} }

{ {b}, {c, a} }

{ {c, a}, {b} }.

В противном случае, если различные упорядочивания множеств считаются различными разбиениями, тогда количество таких упорядоченных разбиений называются упорядоченными числами Белла.

Факторизации

Если число [math]N[/math]является свободным от квадратов, то[math]B_n[/math] показывает количество различных мультипликативных разбиений [math]N[/math]. Если tex dpi="130">N</tex> является квадратичным положительным целым числом (является произведением некоторого числа tex dpi="130">n</tex> различных простых чисел), то tex dpi="130">B_n</tex> дает число различных мультипликативных разбиений[math]N[/math]. Это является факторизацией [math]N[/math] в числа большие, чем 1(рассматривая две факторизации как идентичные, если они имеют одинаковые факторы в другом порядке.) подтверждает это наблюдение Сильвио Минетоле(Principii di Analisi Combinatoria, 1909). Например, 30 является произведением 3 простых чисел 2, 3, and 5, и имеет tex dpi="130">N</tex> = 5 факторизаций:

[math]30 = 2\times 15=3\times 10=5\times 6=2\times 3\times 5[/math]

Схемы рифмовки

Числа Белла показывают количество схем рифмовки tex dpi="130">n</tex>-ой строфы. Схема рифмы описывает, какие строки рифмуются друг с другом, и поэтому может быть истолковано как разбиение множества строк в подмножества рифм. Таким образом, 15 возможных четверостиший схемами рифмовки являются: AAAA, AAAB, AABA, AABB, AABC, ABAA, ABAB, ABAC, ABBA, ABBB, ABBC, ABCA, ABCB, ABCC, and ABCD.

Вычисление с помощью треугольника Пирса

Треугольное множество, правая диагональная последовательность которого состоит из чисел Белла

Числа Белла могут быть с легкостью вычислены с помощью треугольника Белла, который также называют массивом Айткена или треугольником Пирса.

1. Начнем с единицы. Помещаем ее в верхнюю строку. ([math] x_{0,1} = 1 [/math])
2. Каждая новая строка должна начинаться с крайнего правого элемента прошлой строки. ([math]x_{i,1} \leftarrow x_{i-1, r}[/math] где r последний элемент (i-1)-й строки)
3. Определим остальные элементы строки [math]( x_{i,j} \leftarrow x_{i,j-1} + x_{i-1,j-1} )[/math]
4. Повторяем пункт 3, пока [math] j = r + 1 [/math])
5. Крайнее левое число данной строки является числом Белла для этой строки. ([math]B_i \leftarrow x_{i,1}[/math])

Первые пять строк треугольника, построенного по этим правилам:

1
2	3	5
5	7	10	15
15	20	27	37	52

Свойства

Формулы суммирования

Числа Белла удовлетворяют рекуррентному соотношению c участием биномиальных коэффициентов s:

[math]B_{n+1}=\sum_{k=0}^{n} \binom{n}{k} B_k.[/math]

Другая формула суммирования представляет каждое число Белла как сумму чисел Стирлинга второго рода(Stirling numbers of the second kind):

[math]B_n=\sum_{k=0}^n \left\{{n\atop k}\right\}.[/math]

Число Стирлинга [math]\left\{{n\atop k}\right\}[/math] является количеством способов разбиения набора элементов tex dpi="130">n</tex> в ровно tex dpi="130">k</tex> непустых подмножеств. Michael Spivey получил формулу, которая объединяет оба эти суммирования:

[math]B_{n+m} = \sum_{k=0}^n \sum_{j=0}^m \left\{{m\atop j}\right\} {n \choose k} j^{n-k} B_k.[/math]

Производная функция

Экспоненциальной производящей функцией числе Белла является:

[math]B(x) = \sum_{n=0}^\infty \frac{B_n}{n!} x^n = e^{e^x-1}.[/math]

Суммирование используется для определения экспоненциальной производящей функции для любой последовательности чисел. Правая часть является результатом выполнения суммирования в конкретном случае.

Моменты распределения вероятностей

Числа Белла удовлетворяют формуле Добинского

[math]B_n=\frac{1}{e}\sum_{k=0}^\infty \frac{k^n}{k!}.[/math]

Эта формула может быть получена за счет расширения экспоненциальной производящей функции, используя ряд Тейлора(Taylor series) для экспоненциальной функции, а затем собирая условия с аналогичным показателем экспоненты. Это позволяет интерпретировать B_n как tex dpi="130">n</tex>-й момент Пуассоновского распределения с ожидаемым значением 1.

Интегральное представление

Применение интегральной формулы Коши(Cauchy's integral formula) для экспоненциальной производящей функции дает комплексное интегральное представление:

[math] B_n = \frac{n!}{2 \pi i e} \int_{\gamma} \frac{e^{e^z}}{z^{n+1}} \, dz. [/math]

Логарифмическая вогнутость

Числа Белла формируют логарифмически выпуклую последовательность. Деление их на факториал, [math]\frac{B_n}{n!}[/math], дает логарифмически выпуклую последовательность.

Темпы роста

Известно несколько асимптотических формул для чисел Белла. Беренд Тасса в 2010-м установлил следующие границы:

[math] B_n \lt \left( \frac{0.792 n}{\ln( n+1)} \right)^n [/math] для всех положительных чисел [math]n[/math];

кроме того, если [math] \varepsilon\gt 0 [/math] затем для всех [math] n \gt n_0(\varepsilon) [/math],

[math] B_n \lt \left( \frac{e^{-0.6 + \varepsilon} n}{\ln(n+1)}\right)^n [/math]

где [math] ~n_0(\varepsilon) = \max\left\{e^4,d^{-1}(\varepsilon) \right\}~ [/math] и [math] ~d(x):= \ln \ln (x+1) - \ln \ln x + \frac{1+e^{-1}}{\ln x}\,. [/math] Числа Белла могут быть аппроксимированы с помощью функции Ламберта Вт, данная функция имеет такой же темп роста, как логарифм, как

[math]B_n \sim \frac{1}{\sqrt{n}} \left( \frac{n}{W(n)} \right)^{n + \frac{1}{2}} \exp\left(\frac{n}{W(n)} - n - 1\right). [/math]

Moser Wyman установил расширение:

[math]B_{n+h} = \frac{(n+h)!}{W(n)^{n+h}} \times \frac{\exp(e^{W(n)} - 1)}{(2\pi B)^{1/2}} \times \left( 1 + \frac{P_0 + hP_1 + h^2P_2}{e^{W(n)}} + \frac{Q_0 + hQ_1 + h^2Q_2 + h^3Q_3 + h^4Q_4}{e^{2W(n)}} + O(e^{-3W(n)}) \right)[/math]

Асимптотическое выражение

[math] \begin{align} \frac{\ln B_n}{n} & = \ln n - \ln \ln n - 1 + \frac{\ln \ln n}{\ln n} + \frac{1}{\ln n} + \frac{1}{2}\left(\frac{\ln \ln n}{\ln n}\right)^2 + O\left(\frac{\ln \ln n}{(\ln n)^2} \right) \\ & {} \qquad \text{as }n\to\infty \end{align} [/math]

Было установлено де Брайном в 1981 году.

Литература

• Nobuhiro Izumi Hui-Hsiung "Acta Applicandae Texematicae",79–87.Bell numbers, log-concavity, and log-convexity 2000
• Aitken A. C. Edinburgh Texematical Notes,18–23 A problem in combinations 1933
• H. W.BeckerJohn Riordan "The arithmetic of Bell and Stirling numbers" American Journal of Texematics,1948,385–394
• E. T.Bell Exponential polynomials,Annals of Texematics,1934, 258–277
• E. T.Bell The iterated exponential integers,Annals of Texematics,1938,539–557
• Bender Edward A.Williamson, S. Gill, Set Partitions, 319–320, 2006
• Bell numbers

Примeчания

--16:07, 8 октября 2017 (MSK)MikeTerentyev