Конструирование комбинаторных объектов и их подсчёт

Последовательности (Seq)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{z}\}[/math] — множество из различных объектов, [math]S=Seq(A)[/math] — множество всех последовательностей из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{l}\}[/math] — количество объектов веса от [math]1[/math] до [math]l[/math]. Мы считаем, что нет объектов веса [math]0[/math], так как в противном случае существует бесконечное количество последовательностей любого веса. Тогда, количество последовательностей веса [math]n[/math] можно вычислить как [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-i}[/math]. Причем [math]S_{0} = 1[/math], так как есть единственный способ составить пустую последовательность.

[math]\triangleright[/math]

Докажем по индукции. База [math]n = 1[/math]. [math]S_{1}=w_{1} S_{0}=w_{1}[/math], что верно, так как единственный способ составить последовательность веса [math]1[/math] — это взять любой элемент веса [math]1[/math]. Переход. Пусть для [math]j \lt n[/math] верно. Докажем для [math]n[/math]. Возьмем произвольный элемент из [math]A[/math] веса [math]i \leqslant n[/math], и допишем его к последовательности элементов веса [math]n-i[/math]. Образуется новая последовательность веса [math]n[/math]. Причем никакая последовательность не будет учтена дважды, так как прежде не было последовательностей веса [math]n[/math] и ни к какой последовательности меньшего веса мы не добавляем один и тот же элемент дважды.

[math]\triangleleft[/math]

Подсчет битовых векторов длины [math]n[/math]

Пусть [math]A=\{0, 1\}[/math], [math]W=\{2, 0 \ldots 0\}[/math] [math]S=Seq(A)[/math] — множество всех битовых векторов, [math]S_{0}=1[/math].

Тогда, [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-i}=2S_{n-1}=2^{n}[/math].

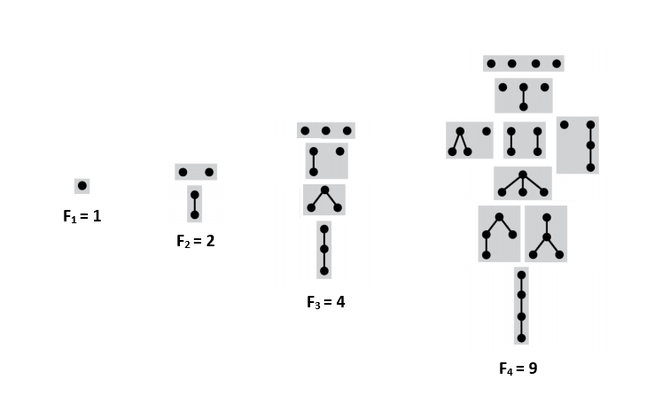
Подсчет Seq из маленьких и больших элементов

Пусть [math]A=\{1, 2\}[/math], [math]W=\{1, 1, 0 \ldots 0\}[/math], [math]S=Seq(A)[/math] — множество всех последовательностей из маленьких и больших элементов, [math]S_{0}=1[/math], [math]S_{1}=1[/math].

Тогда, [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-1}=S_{n-1}+S_{n-2}=F_{n}[/math], где [math]F_{n}[/math] — [math]n[/math]-ое число Фибоначчи .

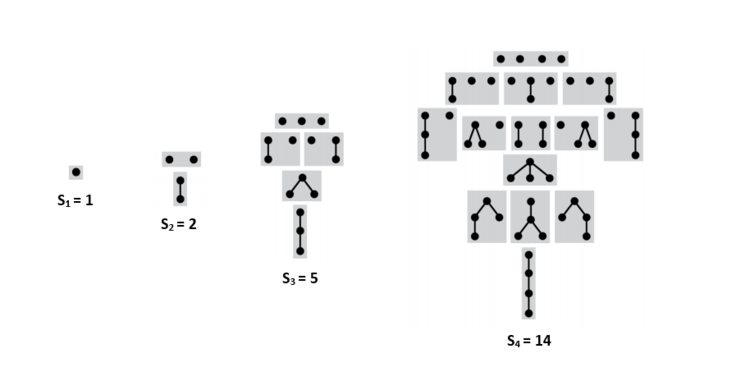
Подсчет подвешенных непомеченных деревьев с порядком на детях

Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами, [math]T_{0} = 1[/math]. [math]S=Seq(A)[/math] — множество всех последовательностей из данных деревьев. [math]S_{n}[/math] — количество последовательностей с суммарным количество вершин [math]n[/math]. Чтобы получить дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину, и подвесить к ней последовательность деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=S_{n-1}[/math].

[math]S_{n}=\sum_{i=1}^{n} T_{i} S_{n-i}=\sum_{i=1}^{n} S_{i-1} S_{n-i}=\sum_{i=0}^{n-1} S_{i} S_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.

Множества (PSet)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{z}\}[/math] — множество из различных объектов, [math]P=PSet(A)[/math] — множество всех множеств, составленных из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{l}\}[/math] — количество объектов веса от [math]1[/math] до [math]l[/math]. Мы также считаем, что нет объектов веса [math]0[/math]. Тогда количество множеств суммарного веса [math]n[/math] можно вычислить как [math]P_{n}=p_{n, n}[/math], где [math]p_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}}{i} p_{n-ik, k-1}[/math] — количество таких множеств, которые содержат объекты, вес которых не больше чем [math]k[/math]. Причем [math]p_{0, i} = 1[/math], так как не набирать никакой вес есть один способ, а [math]p_{i, 0} = 0[/math], [math]i \ne 0[/math], так как нельзя набрать положительный вес из ничего.

[math]\triangleright[/math]

Изначально у нас есть только пустое множество веса [math]0[/math]. Рассмотрим очередной этап вычисления [math]p_{n,k}[/math]. Для данных [math]n[/math] и [math]k[/math] у нас уже имеется множество, которое необходимо дополнить. Мы можем сделать это добавляя от [math]0[/math] до [math]\lfloor \frac{n}{k} \rfloor[/math] элементов веса [math]k[/math] (при условии, что столько различных элементов имеется) в данное множество. Следовательно, у нас образуется новые множества, которые будет необходимо дополнить элементами веса меньше [math]k[/math] (чтобы избежать повторений) суммарного веса [math]n-ik[/math], где [math]i[/math] — количество элементов веса [math]k[/math] которое мы добавили в данное множество. Довольно легко заметить, что данные операции полностью соответствуют описанной выше формуле.

[math]\triangleleft[/math]

Количество PSet из элементов 0 и 1

Пусть [math]A=\{0, 1\}[/math], [math]P=PSet(A)[/math] — множество всех множеств из [math]A[/math], [math]W=\{2, 0 \ldots 0\}[/math], [math]w_{0} = 1[/math]. Тогда [math]P_{n}=p_{n, n}[/math], где [math]p_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} p_{n-ik, k-1}[/math].

[math]P_{0}=p_{0, 0} = 1[/math].

[math]P_{1}=p_{1, 1} = p_{1, 0} + 2p_{0, 0} = 2p_{0, 0} = 2[/math].

[math]P_{2}=p_{2, 2} = p_{2, 1} + 0 \cdot p_{0, 1} = p_{2, 0} + 2p_{1, 0} + p_{0, 0}= p_{0, 0} = 1[/math].

[math]{P_{3}=p_{3, 3} = p_{3, 2} + 0 \cdot p_{0, 2} = p_{3, 1} + 0 \cdot p_{0, 1} = p_{3, 0} + 2p_{2, 0} + 0 \cdot p_{1, 0} + 0 \cdot p_{0, 0}= 0}[/math].

Для [math]n \gt 2[/math], [math]P_{n} = 0[/math] .

[math]\{\}[/math]

[math]\{0\}, \{1\}[/math]

[math]\{0, 1\}[/math]

Количество разбиений на слагаемые

Пусть [math]A=\mathbb{N}[/math], [math]P=PSet(A)[/math] — множество всех разбиений на слагаемые, [math]W=\{1 \ldots 1\}[/math], [math]w_{0} = 1[/math]. Тогда,

[math]P_{n}=p_{n, n}[/math], где [math]p_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} p_{n-ik, k-1} = p_{n, k-1} + p_{n - k, k}[/math], что, как несложно заметить, соответствует формуле, полученной методом динамического программирования.

Мультимножества (MSet)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{z}\}[/math] — множество из различных объектов, [math]M=MSet(A)[/math] — множество всех мультимножеств из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{k}\}[/math] — количество объектов веса [math]\{1 \ldots k\}[/math]. Тогда количество мультимножеств из объектов суммарного веса [math]n[/math] можно вычислить как [math]M_{n}=m_{n, n}[/math], где [math]m_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}+i-1}{i} m_{n-ik, k-1}[/math] — количество таких мультимножеств, которые содержат объекты, вес которых не больше чем [math]k[/math].

[math]\triangleright[/math]

Рассуждения аналогичны рассуждениям [math]PSet[/math], однако теперь мы можем брать один и тот же элемент несколько раз. То есть для подсчета вместо обычных сочетаний нужно использовать сочетания с повторениями.

[math]\triangleleft[/math]

Количество MSet из элементов 0 и 1

Пусть [math]A=\{0, 1\}[/math], [math]S=PSet(A)[/math] — множество всех множеств из [math]A[/math], [math]W=\{2, 0 \ldots 0\}[/math], [math]w_{0} = 1[/math].

Тогда, [math]M_{n}=m_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} s_{n-ik, k-1}[/math]

[math]M_{0}=m_{0, 0} = 1[/math].

[math]M_{1}=m_{1, 1} = m_{1, 0} + 2m_{0, 0} = 2m_{0, 0} = 2[/math].

[math]M_{2}=m_{2, 2} = m_{2, 1} + 0 \cdot m_{0, 1} = m_{2, 0} + 2m_{1, 0} + 3m_{0, 0}= 3m_{0, 0} = 3[/math].

[math]M_{3}=m_{3, 3} = m_{3, 2} + 0 \cdot m_{0, 2} = m_{3, 1} + 0 \cdot m_{0, 1} = m_{3, 0} + 2m_{2, 0} + 3m_{1, 0} + 4m_{0, 0}= 4m_{0, 0} = 4[/math].

[math]\{\}[/math]

[math]\{0\}, \{1\}[/math]

[math]\{0, 0\}, \{0, 1\}, \{1, 1\}[/math]

[math]\{0, 0, 0\}, \{0, 0, 1\}, \{0, 1, 1\}, \{1, 1, 1\}[/math]

[math]{M_{n}=m_{n, n} = m_{n, n-1} + 0 \cdot m_{0, n-1} = m_{n, n-2} + 0 \cdot m_{0, n-2} = \ldots = m_{n, 0} + 2m_{n - 1, 0} + \ldots + nm_{1, 0} + (n+1) m_{0,0} = (n + 1) m_{0,0} = n+1}[/math].

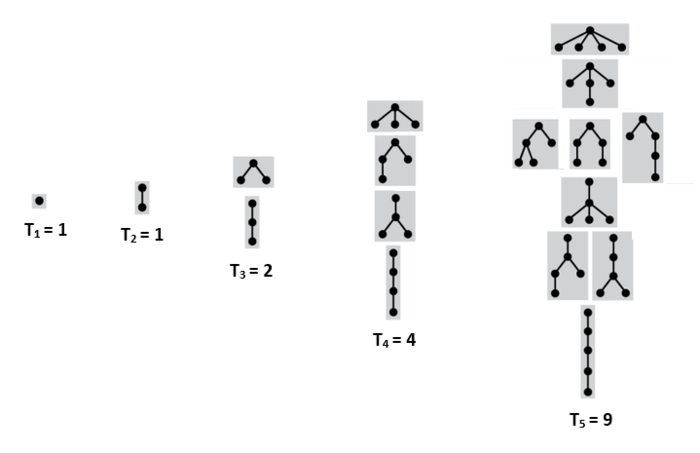
Подсчет подвешенных непомеченных деревьев без порядка на детях

Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами, [math]T_{0} = 1[/math]. [math]F=MSet(T)[/math] — множество всех лесов из данных деревьев, так как лес можно интерпретировать как мультимножество из деревьев. [math]F_{n}=f_{n,n}[/math] — количество лесов с суммарным количество вершин [math]n[/math]. [math]f_{n, k}[/math] — количество таких лесов из [math]n[/math] вершин, что деревья в них содержат не более чем [math]k[/math] вершин. Чтобы получить дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину и подвесить к ней лес деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=F_{n-1}[/math].

[math]F_{n}=f_{n, n}[/math].

[math]f{n,k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{T_{k}+i-1}{i} s_{n-ik, k-1}[/math].

Количество таких деревьев с [math]n[/math] вершинами образуют последовательность [math] 1, 1, 2, 4, 9, 20, 48, 115, 286, 719, 1842, 4766, 12486, 32973, 87811, 235381, 634847 \ldots[/math]

Пары (Pair)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{z}\}[/math], [math]B=\{b_{1},b_{2}, \ldots ,b_{m}\}[/math] — множества из различных объектов, [math]D=Pair(A, B)[/math] — множество всех пар объектов, составленных из элементов [math]A[/math] и [math]B[/math]. [math]W=\{w_{1},w_{2}, \ldots ,w_{k}\}[/math] — количество объектов веса [math]\{1 \ldots k\}[/math], составленных из элементов [math]A[/math], а [math]U=\{u_{1},u_{2}, \ldots ,u_{k}\}[/math] — соответственно для [math]B[/math]. Тогда количество пар из объектов суммарного веса [math]n[/math] можно вычислить как [math]D_{n}=\sum_{i=0}^{n}w_{i}u_{n-i}[/math].

[math]\triangleright[/math]

Чтобы составить пару веса [math]n[/math] нужно взять один элемент веса [math]0 \leqslant i \leqslant n[/math] и элемент веса [math]n-i[/math], что полностью соответствует данной формуле.

[math]\triangleleft[/math]

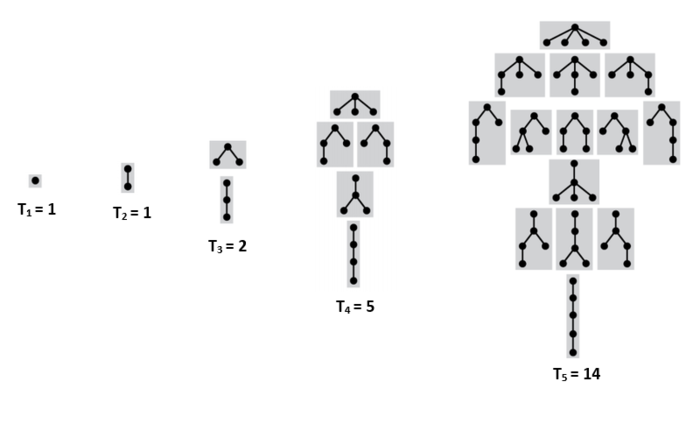
Количество подвешенных неполных двоичных деревьев

Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами, [math]T_{0} = 1[/math]. [math]D=Pair(T, T)[/math] — множество всех пар из данных деревьев. Чтобы получить двоичное дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину и подвесить к ней левого и правого сына с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=D_{n-1}=\sum_{i=0}^{n-1}T_{i}T_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.

Циклы (Cycle)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{z}\}[/math] — множество из различных объектов, [math]C=Cycle(A)[/math] — множество всех циклов из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{m}\}[/math] — количество объектов веса [math]\{1 \ldots m\}[/math]. Тогда количество циклов веса [math]n[/math] можно вычислить как [math]C_{n}=\sum_{s=1}^{n}c_{n, s}[/math], где [math]c_{n,s}[/math] — количество циклов веса [math]n[/math] длины [math]s[/math]. По лемме Бёрнсайда [math]c_{n,s} =\sum_{i=0}^{s-1}\dfrac{|St(\vec{i})|}{s}[/math], где [math]|St(\vec{i})|[/math] — количество стабилизаторов для циклического сдвига на [math]i[/math] .

[math]\triangleright[/math]

Очевидно, что длина цикла веса [math]n[/math] может быть от [math]1[/math] до [math]n[/math]. Посмотрим сколько существует циклов каждой длины. Это можно сделать по лемме Бёрнсайда.

[math]\triangleleft[/math]

Найдем [math]|St(\vec{i})|=z_{n,s,i}[/math] в общем случае.

Пусть [math]g=\mathrm{gcd}(s,i)[/math] — наибольший общий делитель[math](s, i)[/math]. Заметим, что в [math]i[/math]-ой перестановке на [math]j[/math]-ой позиции стоит элемент [math](i + j)\bmod s[/math]. Также, заметим, что элемент [math]a[/math] переходит в элемент [math]a + in[/math], где [math]i = 1, 2, \ldots k[/math]. Из этого следует, что длина цикла для [math]i[/math]-ой перестановки равна [math] \dfrac{\mathrm{lcm}(s, i)}{i} = \dfrac{s}{g}[/math], где [math]\mathrm{lcm}(s, i)[/math] — наименьшее общее кратное[math](s, i)[/math].

Также заметим, что если вес [math]n[/math] нельзя равномерно распределить по всей длине цикла, то стабилизатор равен [math]0[/math].

[math]z_{n, s, i} = \left \{\begin{array}{ll} 0, & n \bmod \frac{s}{g} \neq 0 \\ b_{\frac{ng}{s}, g}, & n \bmod \frac{s}{g} = 0 \end{array} \right. [/math]

Где [math]b_{n,k}[/math] — число способов упорядочить набор из [math]k[/math] элементов суммарного веса [math]n[/math] и

[math]b_{n,k}=\sum_{i=1}^{n}w_{i}b_{n-i, k-1}[/math], причем [math]b_{n,1}=w_{n}[/math].

Задача об ожерельях

Решим данным способом задачу об ожерельях. Пусть необходимый вес [math]n[/math] — это количество бусинок, а [math]k[/math] — количество цветов. Причем каждая бусинка весит [math]1[/math]. То есть [math]W=\{k, 0 \ldots 0\}[/math].

[math]C_{n}=\sum_{s=1}^{n}c_{n,s}=c_{n,n}[/math] так как невозможно набрать вес [math]n[/math] менее, чем [math]n[/math] бусинами при весе бусин [math]1[/math].

[math]c_{n,n}=\sum_{i=0}^{n-1}\dfrac{|St(\vec{i})|}{n}=\dfrac{1}{n}\sum_{i=0}^{s-1}|St(\vec{i})|=\dfrac{1}{n}\sum_{i=0}^{s-1}b_{\mathrm{gcd}(n,i),\mathrm{gcd}(n,i)}[/math]. Поскольку все бусины имеют одинаковый вес [math]1[/math], то [math]b_{n,k} \neq 0[/math]

В итоге, [math]C_{n}=\dfrac{1}{n}\sum_{i=0}^{s-1}k^{\mathrm{gcd}(n,i)}[/math].

Метод производящих функций

Такие большие группы часто анализируют с помощью производящих функций. Один из популярных методов — метод символов (англ. Symbolic method). Он использует внутреннюю структуру объектов для получения производящих функций. В случае непомеченных объектов, как и в анализе в нашей статье, считается что нет объектов нулевого веса. Иногда для удобства их добавляют, чтобы показать наличие одного пустого множества. При непомеченных объектах рассмотренные классы имеют следующие производящие функции:

[math]Seq(A)[/math]	[math]\dfrac{1}{1-A(z)}[/math]
[math]Pset(A)[/math]	[math]\prod\limits_{n \geqslant 1}(1+z^{n})^{A_{n}}=\exp(-\sum\limits_{k \geqslant 1}\dfrac{(-1)^{k}A(z^{k})}{k})[/math]
[math]Mset(A)[/math]	[math]\prod\limits_{n \geqslant 1}\dfrac{1}{(1-z^{n})^{A_{n}}}=\exp(\sum\limits_{k \geqslant 1}\dfrac{A(z^{k})}{k})[/math]
[math]Pair(A,B)[/math]	[math]A(z)B(z)[/math]
[math]Cycle(A)[/math]	[math]\sum\limits_{n \geqslant 1}\dfrac{\phi(n)}n\ln\dfrac{1}{1 - A(z^n)}[/math], где [math]\phi(n)[/math] — функция Эйлера.

Однако порой некоторые комбинаторные классы удобнее обозначать как помеченные. Например, — помеченные графы. С помеченными объектами используется экспоненциальная производящая функция . В данном случае для некоторых рассмотренных классов используются следующие производящие функции:

[math]Seq(A)[/math]	[math]\dfrac{1}{1-A(z)}[/math]
[math]Pset(A)[/math]	[math]\exp(A(z))[/math]
[math]Pair(A,B)[/math]	[math]A(z)B(z)[/math]
[math]Cycle(A)[/math]	[math]\ln\dfrac{1}{1-A(z)}[/math].

См.также

• Лемма Бёрнсайда и Теорема Пойа
• Числа Каталана
• Генерация комбинаторных объектов в лексикографическом порядке

Источники информации

• Philippe Flajolet, Robert Sedgewick, Analytic Combinatorics, 15-92, 2008
• Online Course Materials from Robert Sedgewick
• Wikipedia — Generating function
• Wikipedia — Symbolic method