Левосторонние красно-чёрные деревья — различия между версиями
| Строка 60: | Строка 60: | ||
h = rotateLeft(h); | h = rotateLeft(h); | ||
| − | *Балансировка узла с <tex>4< | + | *Балансировка узла с <tex>4</tex>-я потомками: |
if (isRed(h.left) && isRed(h.left.left)) | if (isRed(h.left) && isRed(h.left.left)) | ||
h = rotateRight(h); | h = rotateRight(h); | ||
| − | + | ===Псевдокод=== | |
'''void''' insert( '''key''' : Key, '''value''' : Value ): | '''void''' insert( '''key''' : Key, '''value''' : Value ): | ||
root = insert(root, key, value) | root = insert(root, key, value) | ||
| Строка 90: | Строка 90: | ||
'''if''' isRed(h.right) '''&&''' '''!'''isRed(h.left) | '''if''' isRed(h.right) '''&&''' '''!'''isRed(h.left) | ||
h = rotateLeft(h) | h = rotateLeft(h) | ||
| − | ////Балансировка узла с <tex>4< | + | ////Балансировка узла с <tex>4</tex>-я потомками |
'''if''' isRed(h.left) '''&&''' isRed(h.left.left) | '''if''' isRed(h.left) '''&&''' isRed(h.left.left) | ||
h = rotateRight(h) | h = rotateRight(h) | ||
Версия 02:29, 14 марта 2018
| Определение: |
| Left-leaning Red-Black Trees — модификация красно-черных деревьев, имеющая ряд преимуществ на классической структурой. Разработана Робертом Соджевиском в 2008 году. |
Содержание
Преимущества
- необходимо менее 80 строчек кода для реализации структуры
- более быстрая вставка, удаление элементов
- простота
Вращения
Чтобы поддерживать красно-черные двоичное деревья поиска необходимо соблюдать следующие инвариантные свойства при вставке и удалении:
- Ни один обход от корня до листьев дерева не содержит двух последовательных красных узлов.
- Количество черных узлов на каждом таком пути одинаково.
Из этих инвариантов следует, что длина каждого пути от корня до листьев в красно-черном дереве с узлами не превышает .
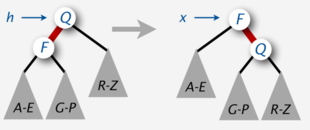
Основные операции, используемые алгоритмами сбалансированного дерева для поддержания баланса при вставке и удалении, называются вращениями. Эти операции трансформируют -узел,левый потомок которого окрашен в красный, в -узел, правый потомок которого окрашен в красный и наоборот. Вращения сохраняют два указанных выше инварианта, не изменяют поддеревья узла.
Псевокод
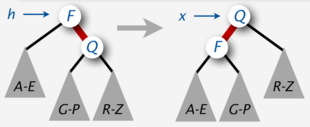
Node rotateRight( h : Node) :
x = h.left
h.left= x.right
x.right= h
x.color = h.color
h.color = RED
return x
Node rotateLeft( h : Node) :
x = h.right
h.right = x.left
x.left = h
x.color = h.color
h.color = RED
return x
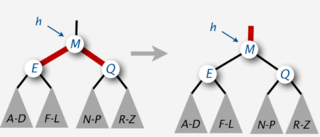
Переворот цветов
В красно-черных деревьях используется такая операция как , которая инвертирует цвет узла и двух его детей. Она не изменяет количество черных узлов при любом обходе от корня до листьев дерева, но может привести к появлению двух последовательных красных узлов.
void flipColors( h : Node h) :
h.color = ! h.color
h.left.color = ! h.left.color
h.right.color = h.right.color
Вставка
Вставка в LLRB базируется на протых операциях:
- Вставка нового узла к листу дерева:
if (h == null)
return new Node(key, value, RED);
- Расщепление узла с -я потомками:
if (isRed(h.left) && isRed(h.right))
colorFlip(h);
- Принудительное вращение влево:
if (isRed(h.right))
h = rotateLeft(h);
- Балансировка узла с -я потомками:
if (isRed(h.left) && isRed(h.left.left))
h = rotateRight(h);
Псевдокод
void insert( key : Key, value : Value ):
root = insert(root, key, value)
root.color = BLACK
Node insert( h : Node, key : Key, value : Value):
//Вставка нового узла к листу дерева
if h == null
return new Node(key, value)
//Расщепление узла с -я потомками
if isRed(h.left) && isRed(h.right)
colorFlip(h)
//Стандартная вставка в дереве поиска
int cmp = key.compareTo(h.key)
if cmp == 0
h.val = value
else
if cmp < 0
h.left = insert(h.left, key, value)
else
h.right = insert(h.right, key, value)
//Принудительное вращение влево
if isRed(h.right) && !isRed(h.left)
h = rotateLeft(h)
////Балансировка узла с -я потомками
if isRed(h.left) && isRed(h.left.left)
h = rotateRight(h)
return h
Value search(key : Key):
Node x = root
while x != null
int cmp = key.compareTo(x.key)
if cmp == 0
return x.val
else
if cmp < 0
x = x.left
else
if cmp > 0
x = x.right
return null
Удаление
f cient implementation of the delete operation is a challenge in many symbol-table implementa- tions, and red-black trees are no exception. Industrial-strength implementations run to over 100 lines of code, and text books generally describe the operation in terms of detailed case studies, eschewing full implementations. Guibas and Sedgewick presented a delete implementation in [7], but it is not fully speci ed and depends on a call-by-reference approach not commonly found in modern code. The most popular method in common use is based on a parent pointers (see [6]), which adds substantial overhead and does not reduce the number of cases to be handled. The code on the next page is a full implementation of for LLRB 2-3 trees. It is based on the reverse of the approach used for insert in top-down 2-3-4 trees: we perform rotations and color ips on the way down the search path to ensure that the search does not end on a 2-node, so that we can just delete the node at the bottom. We use the method to share the code for the color ip and rotations following the recursive calls in the code.With , we can leave right-leaning red links and unbalanced 4-nodes along the search path, secure that these conditions will be xed on the way up the tree. (The approach is also effective 2-3-4 trees, but requires an extra rotation when the right node off the search path is a 4-node.) As a warmup, consider the delete-the-minimum operation, where the goal is to delete the bottom node on the left spine while maintaining balance. To do so, we maintain the invariant that the current node or its left child is red. We can do so by moving to the left unless the current node is red and its left child and left grandchild are both black. In that case, we can do a color ip, which restores the invariant but may introduce successive reds on the right. In that case, we can correct the condition with two rotations and a color ip. These operations are implemented in the method on the next page. With , the recursive implementation of above is straightforward. For general deletion, we also need , which is similar, but simpler, and we need to rotate left-leaning red links to the right on the search path to maintain the invariant. If the node to be deleted is an internal node, we replace its key and value elds with those in the minimum node in its right subtree and then delete the minimum in the right subtree (or we could rearrange pointers to use the node instead of copying elds). The full implementation of that dervies from this discussion is given on the facing page. It uses one-third to one-quarter the amount of code found in typical implementations. It has been demonstrated before [2, 11, 13] that maintaining a eld in each node containing its height can lead to code for delete that is similarly concise, but that extra space is a high price to pay in a practical implementation. With trees, we can arrange for concise code having a logarithmic performance guarantee and using no extra space.
void deleteMin() root = deleteMin(root); root.color = BLACK;
Node deleteMin(h : Node)
if (h.left == null) return null;
if !isRed(h.left) && !isRed(h.left.left)
h = moveRedLeft(h);
h.left = deleteMin(h.left);
return fixUp(h);
Delete-the-minimum code for LLRB 2-3 trees
void deleteMin(): root = deleteMin(root) root.color = BLACK
Node deleteMin( h : Node):
if h.left == null
return null
if !isRed(h.left) && !isRed(h.left.left)
h = moveRedLeft(h)
h.left = deleteMin(h.left)
return fixUp(h)
Node moveRedLeft(Node : h):
colorFlip(h):
if isRed(h.right.left)
h.right = rotateRight(h.right)
h = rotateLeft(h)
colorFlip(h)
return h
Node moveRedRight(h :Node ):
colorFlip(h)
if isRed(h.left.left))
h = rotateRight(h)
colorFlip(h)
return h
void delete(key : Key): root = delete(root, key) root.color = BLACK
Node delete(Node : h, Key : key):
if key.compareTo(h.key) < 0)
if !isRed(h.left) && !isRed(h.left.left)
h = moveRedLeft(h)
h.left = delete(h.left, key)
else
if isRed(h.left)
h = rotateRight(h)
if key.compareTo(h.key) == 0 && (h.right == null)
return null
if !isRed(h.right) && !isRed(h.right.left)
h = moveRedRight(h)
if key.compareTo(h.key) == 0
h.val = get(h.right, min(h.right).key)
h.key = min(h.right).key
h.right = deleteMin(h.right)
else
h.right = delete(h.right, key)
return fixUp(h)